Vektörlerin Toplanmasında Kullanılan Yöntemler 9. Sınıf Fizik
9. Sınıf Vektörlerin Toplanmasında Kullanılan Yöntemler Testleri
9. Sınıf Vektörlerin Toplanmasında Kullanılan Yöntemler Ders Notu (Yeni Müfredat)
Vektörlerin toplanması, fiziksel büyüklüklerin hem yön hem de büyüklüğe sahip olduğu durumlarda kullanılır. Bu konu, özellikle kuvvet, hız ve ivme gibi büyüklüklerin nasıl birleştirileceğini anlamada önemlidir. Vektörlerin toplanmasında üç temel yöntem kullanılır: uç uca ekleme, paralelkenar yöntemi ve bileşenlerine ayırma yöntemi.
Vektörel niceliklerin yönü olduğundan, vektörel işlemlerde skaler niceliklerdeki işlemlerden farklı yöntemler kullanılır. İki ya da daha fazla vektörün toplanmasıyla elde edilen vektöre bileşke vektör denir. Bileşke vektör genellikle R ile gösterilir.
Toplanan vektörlerin yönleri aynı ise bileşke vektörün büyüklüğü, vektörlerin skaler toplamı ile bulunur. Vektörlerin yönleri zıt ise bileşke vektörün büyüklüğü, vektörlerin skaler farkı ile bulunur.
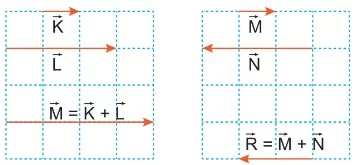
Paralelkenar Yöntemi
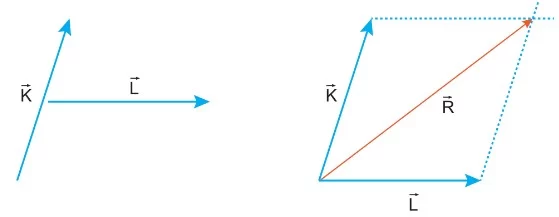
Toplanacak vektörlerin öncelikle başlangıç noktaları birleştirilir. Daha sonra her bir vektörün ucundan diğer vektöre paralel çizgiler çizilir. Böylelikle bir paralelkenar oluşturulur. Vektörlerin başlangıcından paralelkenarın diğer köşesine çizilen vektör, bileşke vektördür.
Bileşkesi bulunacak vektörlerin sayısı ikiden fazla ise paralelkenar yöntemi çok kullanışlı bir yöntem değildir. Çünkü paralelkenar yönteminde vektörler ikişer ikişer toplanmalıdır. Vektörlerin toplanmasında uç uca ekleme (çokgen) yöntemi, paralelkenar yöntemine göre daha kullanışlı bir yöntemdir.
Uç Uca Ekleme Yöntemi
Şekil I’deki K, L, M vektörlerinin bileşkesi bulunurken, vektörlerin yönü ve doğrultusu değiştirilmeden birinin bitiş noktasına diğerinin başlangıç noktası gelecek biçimde Şekil II’deki gibi çizilir. Daha sonra ilk vektörün başlangıç noktasından en son eklenen vektörün bitiş noktasına kadar bileşke (R) vektörü çizilir. Çizilen vektörün uzunluğu hesaplanarak bileşke vektörün büyüklüğü bulunur.
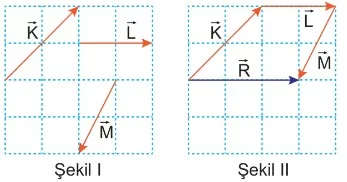
Bileşke vektör bulunurken vektörlerin uç uca eklenme sırası önemli değildir. Vektörler farklı bir sırayla toplansa da bileşke vektörün yönü ve büyüklüğü değişmez.
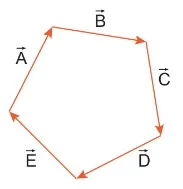
Vektörler uç uca eklendiğinde son vektörün bitiş noktası, ilk vektörün başlangıç noktasına geliyorsa, bileşke vektör sıfırdır. Şekildeki A, B, C, D ve E vektörlerinin bileşkesi sıfırdır.
Vektörlerin Bileşenlerine Ayırma Yöntemiyle Toplanması
Vektörlerin bileşkesini bulmanın bir diğer yolu da, her bir vektörün bileşenlerini hesaplayıp toplamaktır.
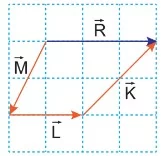
A, B ve C vektörlerinin her birinin bileşenlerinin koordinatları bulunur.
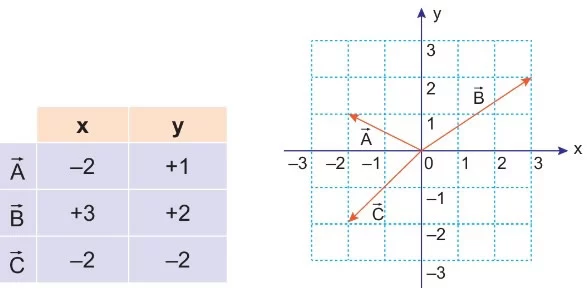
Bileşkenin x ve y bileşenleri: Rx = -2 + 3 – 2 = -1
Ry = +1 + 2 – 2 = +1
Bileşkenin koordinatları (-1, +1) bulunur.
Bileşke bulunurken bileşenlerin yönleri gösterildikten sonra aynı yönlü bileşenler toplanıp, zıt yönlü bileşenler çıkarıldıktan sonra bileşkenin bileşenleri bulunabilir.
A vektörünün bileşenleri sola 2 birim, yukarı 1 birim.
B vektörünün bileşenleri sağa 3 birim, yukarı 2 birim.
C vektörünün bileşenleri sola 2 birim, aşağı 2 birim.
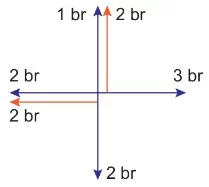
Bileşkenin bileşenleri yukarı yönde 1 birim ve sola doğru 1 birim bulunur.
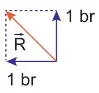
Özet:
1. Uç Uca Ekleme Yöntemi
Bu yöntemde, birinci vektör çizilir ve ikinci vektör, birincinin bitiş noktasından başlayacak şekilde yerleştirilir. Aynı şekilde diğer vektörler de sırasıyla eklenir. Sonuçta, ilk vektörün başlangıç noktasından son vektörün bitiş noktasına kadar çizilen doğru, toplam vektörü gösterir. Bu yöntem, vektörlerin birbirine ardışık eklenmesi şeklinde olduğu için basit ve görsel bir yöntemdir.
Örnek: Eğer bir kişi doğuya doğru 3 metre, ardından kuzeye doğru 4 metre yürüyorsa, kişinin toplam yer değiştirmesi iki vektörün uç uca eklenmesiyle bulunur. Sonuçta, kişinin başlangıç noktası ile bitiş noktası arasındaki doğru, yer değiştirme vektörüdür.
2. Paralelkenar Yöntemi
Bu yöntemde, iki vektör aynı başlangıç noktasından çizilir. Vektörlerin paralel kenarları çizilerek bir paralelkenar oluşturulur. Paralelkenarın köşegeni, bu iki vektörün toplamını verir. Bu yöntem, aynı anda uygulanan iki kuvvetin ya da iki farklı yönlü hızın toplamını bulmak için kullanılır.
Örnek: İki kuvvet aynı cisme farklı yönlerden uygulanıyorsa, paralelkenar yöntemi ile bu kuvvetlerin bileşkesi bulunabilir. Çizilen köşegen, cisme uygulanan net kuvveti gösterir.
3. Bileşenlerine Ayırma Yöntemi
Bu yöntem, vektörlerin dik bileşenlerine ayrılarak toplanması esasına dayanır. Her vektör x ve y bileşenlerine ayrılır. Aynı eksendeki bileşenler toplanır ve elde edilen bileşenler sonucunda toplam vektör bulunur. Bu yöntem, genellikle farklı yönlere bakan vektörlerin toplamını bulmada kullanılır.
Örnek: Bir cisim eğik bir yüzeyde kayıyorsa, hız vektörü yatay ve dikey bileşenlerine ayrılarak toplanabilir.
Bu yöntemler, vektörlerin büyüklük ve yönlerinin doğru şekilde birleştirilmesini sağlar ve fiziksel problemlerin çözümünde önemli bir yer tutar.





