Vektörler konu anlatımı 9. sınıf matematik
Vektörler konu anlatımı videoları
Vektörler Konu Anlatımı
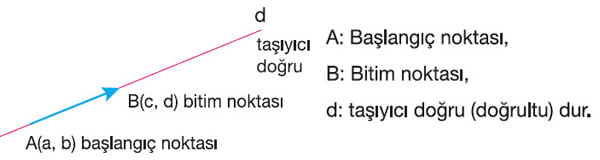
Yönlü Doğru Parçası: Uç noktalarından biri başlangıç noktası, diğeri bitim noktası olarak seçilen bir doğru parçasına yönlü doğru parçası denir. Başlangıç noktası A, bitim noktası B olan yönlü doğru parçası 
şeklinde gösterilir ve AB yönlü doğru parçası diye okunur. AB yönlü doğru parçasının üzerinde bulunduğu doğruya taşıyıcı doğru denir.
AB yönlü doğru parçasının A ve B noktaları arasındaki uzaklığa AB yönlü doğru parçasının uzunluğu denir.
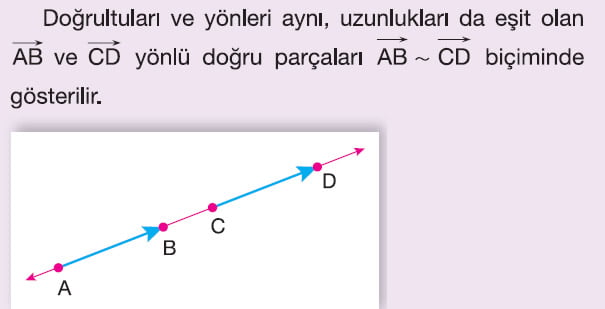
Doğrultuları ve yönleri aynı, uzunlukları eşit olan yönlü doğru parçalarına eş yönlü doğru parçaları denir.
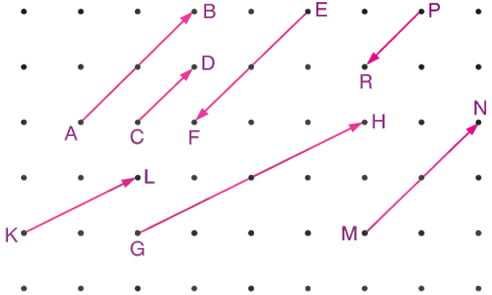
Örnek: Aşağıdaki noktalı kağıt üzerinde verilen yönlü doğru parçalarından hangileri eş yönlü doğru parçalarıdır.
Çözüm:
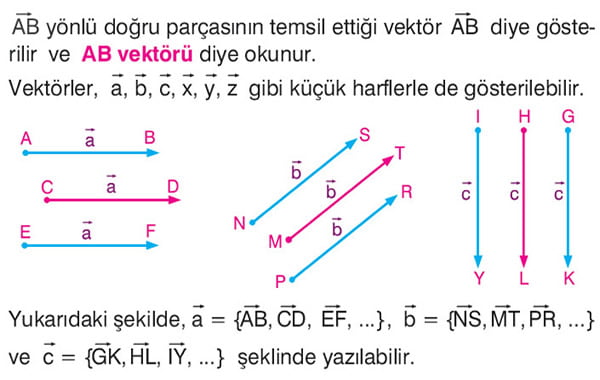
Vektör: Eş yönlü doğru parçalarını temsil eden yönlü doğru parçasına vektör denir.
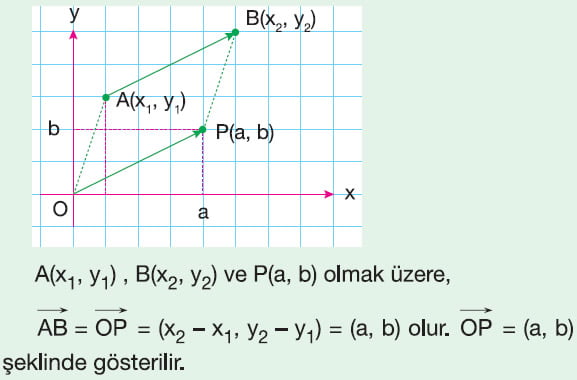
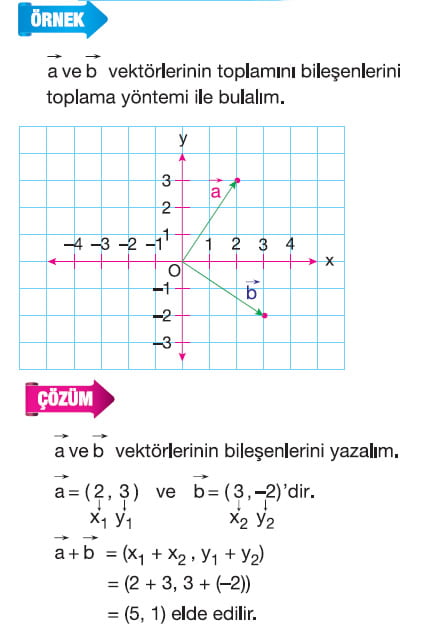
Bir Vektörün Bileşenleri: Başlangıç noktası A(a, b) ve bitim noktası B(c, d) olan AB vektörünün bileşenleri (c-a, d-b) şeklinde ifade edilir.
= (c-a, d-b)
Konum (Yer) Vektörü: Başlangıç noktası orjinde (0, 0) olan vektöre konum vektörü denir.
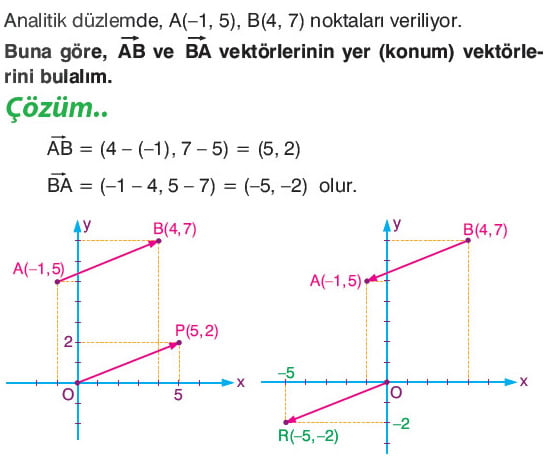
Örnek: A(5, -2) ve B(7, 1) noktaları veriliyor. Buna göre vektörünün bileşenlerini bulunuz.
Çözüm: = (7-5, 1-(-2)) = (5, 1+2) = (5, 3)
Örnek:
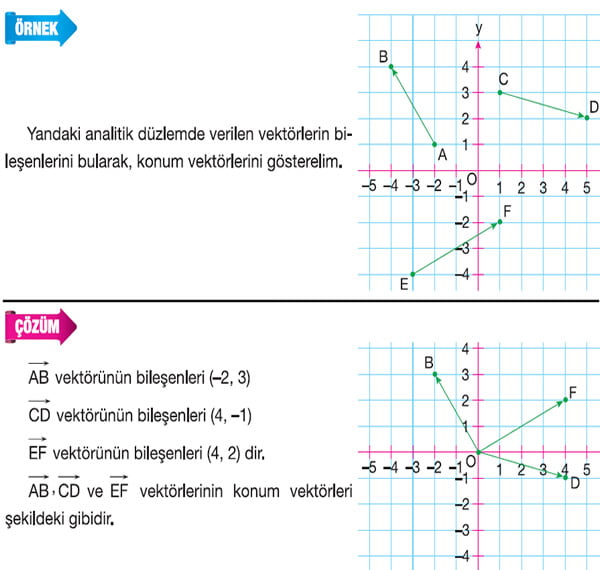
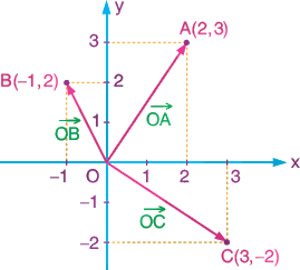
Örnek: Analitik düzlemde A(2, 3), B(-1, 2) ve C(3, -2) noktalarının yer vektörlerini çizelim.
Çözüm:
Vektörler konu anlatımı videosu konu başlıkları,
- Vektör nedir tanımı
- Vektörlerde toplama ve çıkarma işlemi
- Analitik düzlemde vektörler ve konum vektörü
- Bir vektörün uzunluğu (Normu)
- İki vektörün eşitliği
- Bir vektörün bir gerçek sayı ile çarpılması
- Standart birim vektörler (Temel veya baz vektörler)
- Vektörlerin lineer bileşimi
- Vektörlerde iç çarpım (Skaler çarpım)
- İç çarpımın geometrik yorumu
Vektörler konu anlatımı 9. sınıf matematik videolu
Birim Vektör: Uzunluğu bir birim olan vektöre birim vektör denir.
Sıfır Vektörü: Başlangıç ve bitim noktaları aynı olan vektöre sıfır vektörü denir. Sıfır vektörünün uzunluğu sıfırdır.
Dik Vektörler: Düzlemde başlangıç noktaları aynı ve aralarındaki açı 90 derece olan vektörlere dik vektörler denir.
Zıt (Ters) Vektörler: Doğrultuları aynı yönleri zıt olan vektörlere zıt vektörler denir.
Bir u vektörü k=0 sayısı ile çarpılırsa sıfır vektörü elde edilir. Vektör sıfırdan büyük bir k sayısı ile çarpılırsa vektörün yönü ve doğrultusu aynı kalır. Sıfırdan küçük bir k sayısı ile çarpılırsa vektörün doğrultusu aynı kalır, yönü ise zıt olur. Bir vektörü k reel sayısı ile çarparsak bileşenlerinin ikisini de bu k sayısı ile çarpmamız gerekir.
Bir yönlü doğru parçasının başlangıç ve bitim noktaları arasındaki uzaklığa vektörün uzunluğu denir.
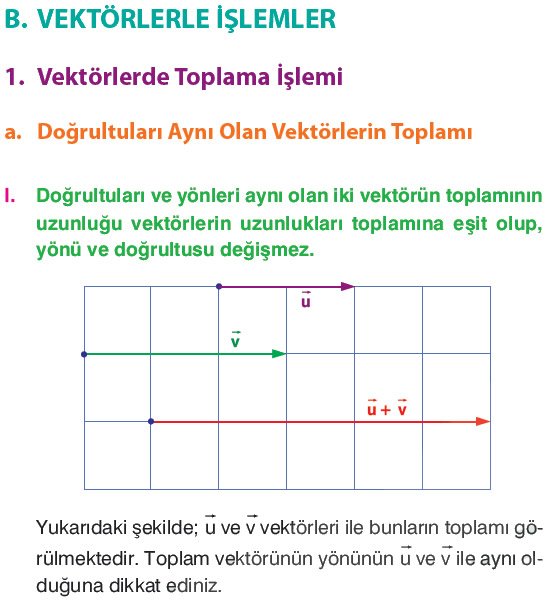
Doğrultuları ve yönleri aynı olan iki vektörün toplamının uzunluğu vektörlerin uzunlukları toplamına eşit olup, yönü ve doğrultusu değişmez.
Doğrultuları aynı, yönleri farklı olan iki vektörün toplamının uzunluğu, vektörlerin uzunlukları farkına eşit olup yönü büyük olan vektörle aynıdır. Doğrultusu ise değişmez.
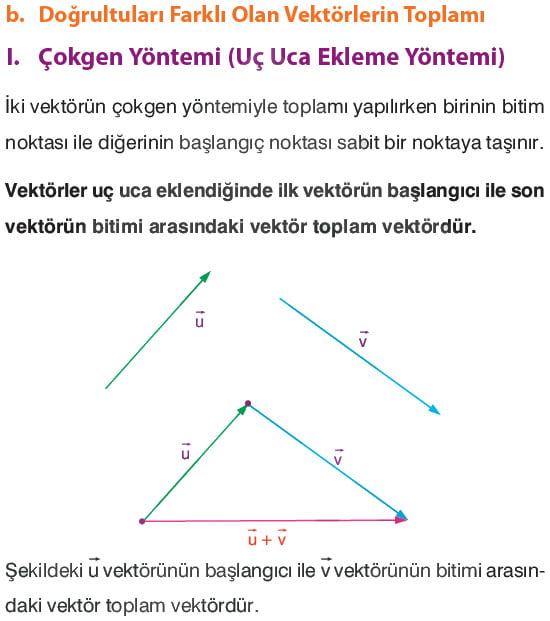
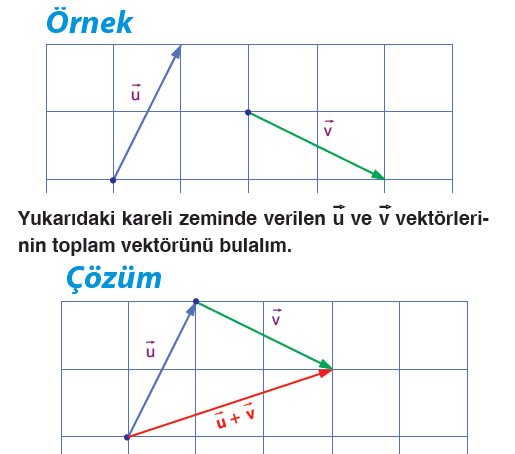
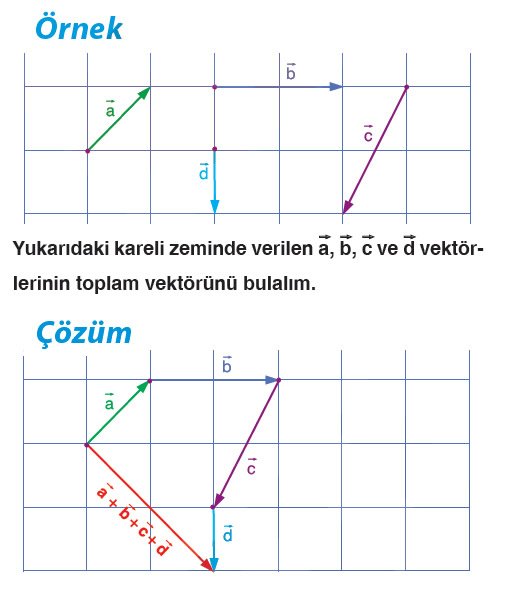
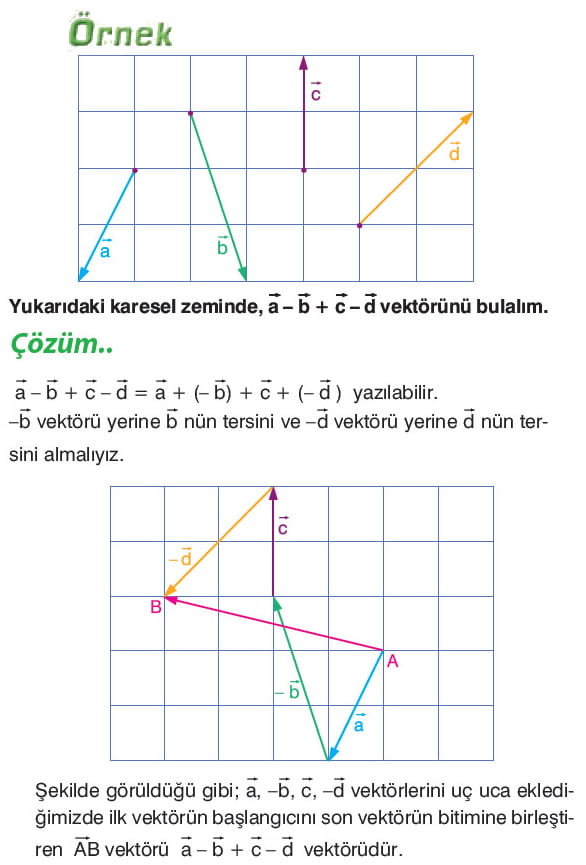
İki vektörün çokgen yöntemiyle toplamı yapılırken birinin bitim noktası ile diğerinin başlangıç noktası sabit bir noktaya taşınır. Vektörler uç uca eklendiğinde ilk vektörün başlangıcı ile son vektörün bitimi arasındaki vektör toplam vektörüdür.
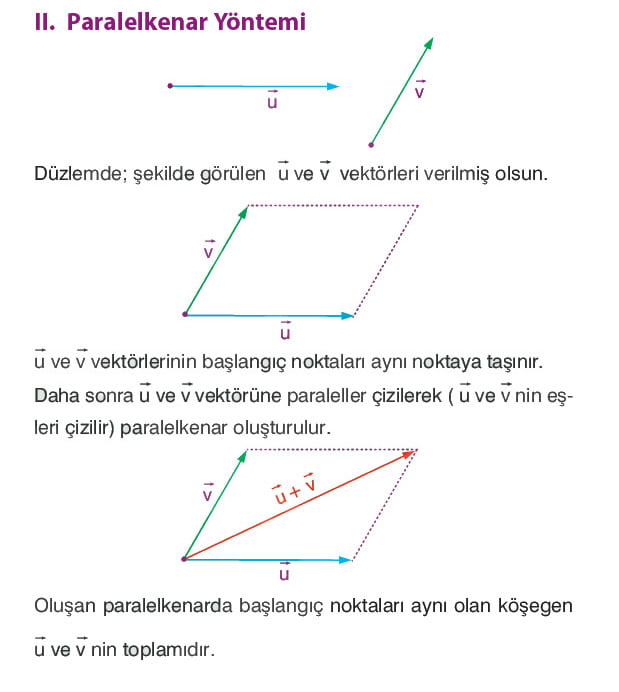
Vektörlerin başlangıç noktaları birleştirilir ve paralelkenar oluşturulur. Oluşan paralelkenarda başlangıç noktasından çizilen köşegen toplam vektörüdür.
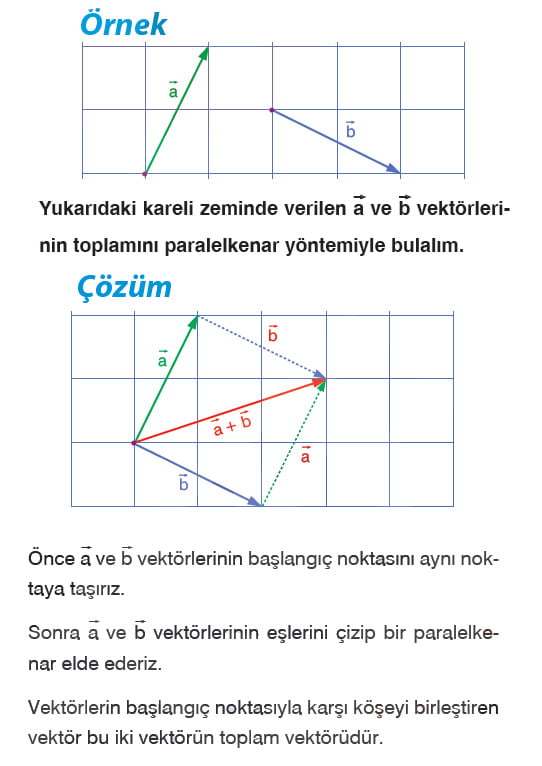
Önce a ve b vektörlerinin başlangıç noktasını aynı noktaya taşırız. Sonra a ve b vektörlerinin eşlerini çizip bir paralelkenar elde ederiz. Vektörlerin başlangıç noktasıyla karşı köşeyi birleştiren vektör bu iki vektörün toplamıdır.