Vektörler konusu, 9. sınıf fizik müfredatında yön ve büyüklüğe sahip büyüklüklerin incelenmesinde kullanılır. Fizikte birçok büyüklüğün yönlü olduğu durumlarda vektörlerin nasıl temsil edileceği, toplanacağı ve çıkarılacağı öğrenilir. Bu konu, kuvvet, hız, ivme gibi yönü olan fiziksel büyüklüklerin anlaşılmasında önemlidir.
9. Sınıf Vektörler Testleri
9. Sınıf Vektörler Ders Notu (Yeni Müfredat)
Vektör Nedir?
Yönü ve büyüklüğü olan doğru parçalarına vektör adı verilir. Vektörlerin belirleyici unsurları şunlardır:
- Başlangıç ve bitiş noktaları,
- Yönü,
- Doğrultusu,
- Şiddeti (yani büyüklüğü, sayısal değeri).
Vektörler, temsil edilen harf veya sembolün üzerine çizilen bir okla gösterilir. Vektörün büyüklüğü, genellikle 
veya A olarak belirtilir. Örneğin, bir vektörünün özellikleri aşağıda sıralanmıştır.
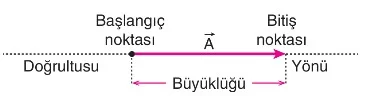
a) Büyüklük (Şiddet)
Bir vektörün büyüklüğü, vektörün uzunluğu ile orantılı olarak çizilir. Örneğin, 
vektörünün büyüklüğü 
olarak ifade edilir.
b) Doğrultu
Vektörün doğrultusu, üzerinde bulunduğu sonsuz uzunluktaki bir çizgidir. Örneğin, 
vektörleri doğu-batı doğrultusunda olabilir.
c) Yön
Vektörün yönü, ok işaretinin gösterdiği tarafa göre belirlenir. Örneğin, 
batıya doğru yönelmişken, 
doğuya doğru yönelmiştir.
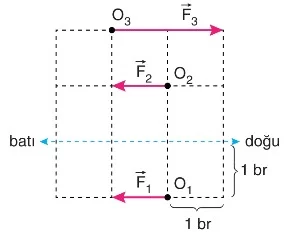
d) Başlangıç Noktası
vektörünün O1 noktası, 
vektörünün O2 noktası, vektörünün O3 noktası başlangıç noktasıdır.
K, L, M ve N vektörlerine ait büyüklük, yön ve doğrultu özellikleri aşağıda belirtilmiştir.
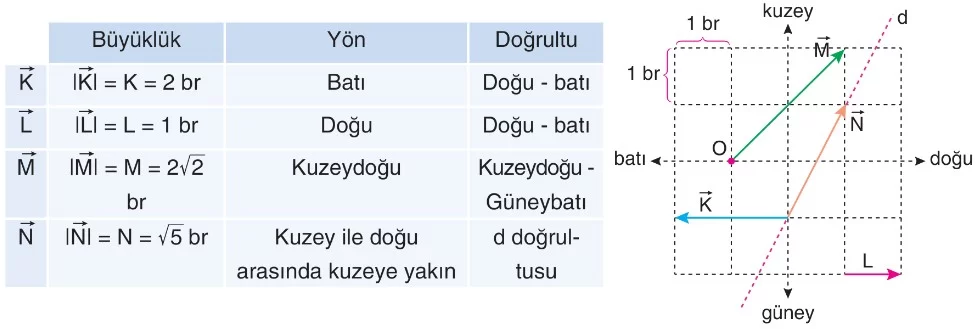
- ile vektörlerinin yönleri ters ve doğrultuları aynıdır.
- M ile N vektörlerinin yön ve doğrultuları farklıdır.
Eşit Vektörler
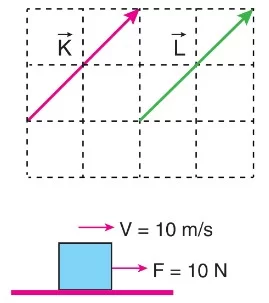
- Aynı niceliğe ait, yönleri ve büyüklükleri aynı olan vektörlere eşit vektörler denir.
- Değerleri sayısal olarak aynı olan vektörlerin birimleri farklı ise vektörler birbirine eşit değildir.
- Kuvvet ve hız farklı fiziksel niceliği belirten vektörel büyüklüklerdir. Kuvvet değeri F=10 N, hız değeri V=10 m/s olduğunda kuvvet ve hız vektörleri birbirine eşittir denilemez. F≠V
Zıt Vektörler
Aynı niceliğe ait büyüklükleri eşit, aynı doğrultuda, yönleri zıt olan vektörlere zıt vektörler denir. Birim karelere bölünmüş yandaki düzlemde ve Z vektörleri verilmiştir.
Zıt vektör ile zıt yönlü vektör karıştırılmamalıdır. Zıt vektörlerin büyüklükleri eşit olmalıdır.
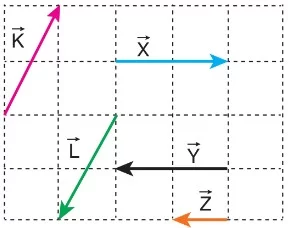
Not: Zıt yönlü vektör ile zıt vektörler farklı anlamdadır. Zıt vektörler aynı büyüklükte ve zıt yönlüdür. Zıt yönlü vektörlerin büyüklüklerinin aynı olmasına gerek yoktur.
- X ile Z zıt vektör olmayıp zıt yönlü vektördür.
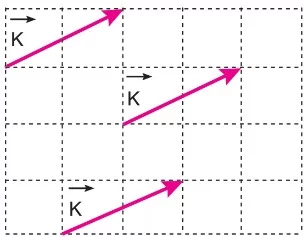
- Bir vektör yönü ve büyüklüğü değiştirilmeden aynı düzlemde bir yerden başka bir yere taşınabilir. Bu durumda vektörün özelliği değişmez.
- Şekilde verilen K vektörü, farklı yerlere taşınmış olmasına rağmen yön, doğrultu ve büyüklüğü değişmediğinden K vektörü de değişmemiştir.
Bir Vektörün Reel Bir Sayıyla Çarpılması
Bir vektörün reel bir sayıyla çarpılması işlemi sonucunda yine bir vektör elde edilir. Ancak vektörün yönü ya da büyüklüğü değişebilir, doğrultusu kesinlikle değişmez.
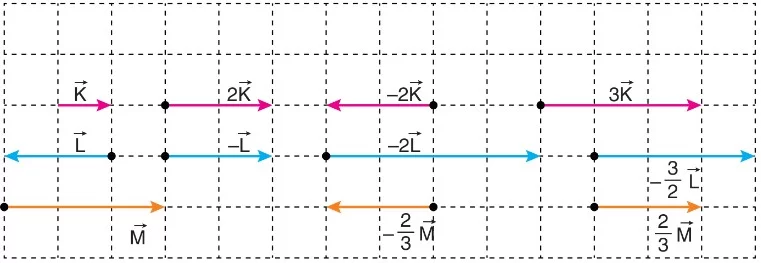
Özet:
Vektörlerin Temel Kavramları
- Skaler ve Vektörel Büyüklükler
- Skaler büyüklükler: Sadece büyüklüğe sahip olan fiziksel niceliklerdir. Örneğin, zaman, sıcaklık, kütle gibi nicelikler skaler büyüklüklerdir.
- Vektörel büyüklükler: Hem büyüklüğü hem de yönü olan fiziksel niceliklerdir. Kuvvet, hız, ivme gibi büyüklükler vektörel büyüklüklere örnektir.
- Vektörün Gösterimi Vektörler bir doğru üzerinde okla gösterilir. Vektörün uzunluğu büyüklüğü, oku ise yönünü temsil eder. Bir vektörün başlangıç noktası ve bitiş noktası vardır.
- Vektörlerin Bileşenleri Bir vektör, yatay ve dikey bileşenlerine ayrılarak temsil edilebilir. Bu bileşenler, genellikle x ve y eksenine göre hesaplanır.
Vektörlerin Toplanması Yöntemleri
- Uç Uca Ekleme Yöntemi Bu yöntemde, birinci vektörün bitiş noktasına ikinci vektör eklenir. Vektörlerin toplamı, ilk vektörün başlangıcından son vektörün bitişine kadar olan doğrultuda çizilir. Bu yöntemle iki ya da daha fazla vektör ardışık olarak birleştirilir.Örnek: A vektörü 5 metre doğuya, B vektörü 3 metre kuzeye yönelmişse, toplam vektör A ve B’nin uç uca eklenmesiyle bulunur.
- Paralelkenar Yöntemi Bu yöntemde, iki vektör aynı başlangıç noktasından çıkarak bir paralelkenar oluşturulur. Paralelkenarın köşegeni, bu iki vektörün toplamını (bileşkesini) verir. Aynı anda uygulanan iki kuvvetin ya da hızın bileşkesini bulmak için kullanılır.Örnek: İki kuvvet, aynı cisme farklı yönlerden uygulanıyorsa, bu kuvvetlerin bileşkesi paralelkenar yöntemiyle bulunabilir.
- Bileşenlerine Ayırma Yöntemi Vektörler yatay ve dikey bileşenlerine ayrılarak toplanır. Her vektörün x ve y bileşenleri ayrı ayrı hesaplanır. Aynı eksendeki bileşenler toplanır ve sonuçta toplam vektör elde edilir.Örnek: Bir vektör 60 derece açı yaparak hareket eden bir cismi temsil ediyorsa, bu vektörün x ve y bileşenleri bulunarak toplam vektör hesaplanabilir.
Vektörlerin Çıkarılması
Vektörlerin çıkarılması, bir vektörün tersinin alınarak toplanması şeklinde yapılır. Örneğin, A vektöründen B vektörünü çıkarmak, A’ya B’nin tersini eklemekle aynıdır.
Vektörler, yön ve büyüklüğe sahip olan fiziksel büyüklüklerin doğru şekilde analiz edilmesini sağlar. Vektörlerin doğru bir şekilde toplanması, çıkarılması ve bileşenlerine ayrılması, fiziksel olayları anlamada büyük önem taşır.
