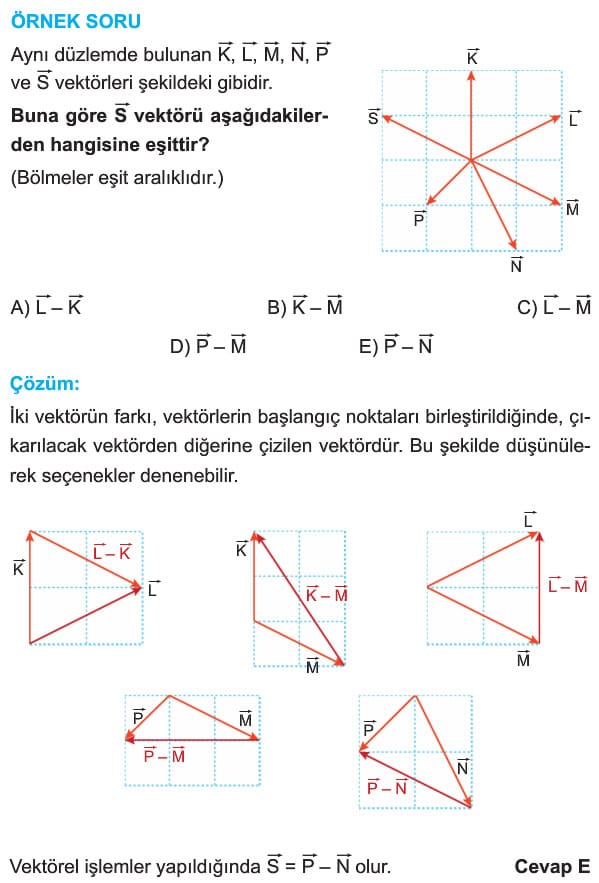
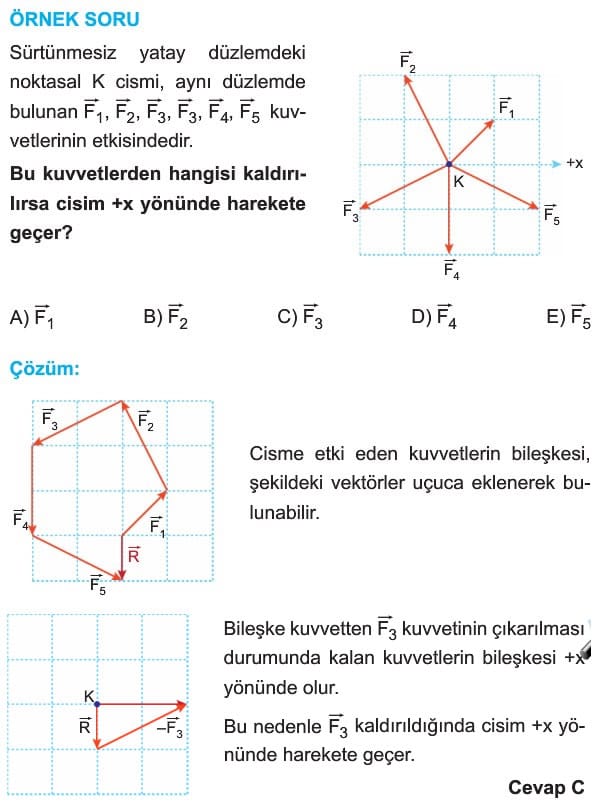
Vektörler 11. Sınıf Fizik
Bu yazımızda 11. Sınıf Matematik Mantık Ünitesinin “Vektörler” konusunun ders notları bulunmaktadır. Ders notlarını bitirdikten sonra Vektörler ünitesi ile ilgili online testler çözebilirsiniz.
11. Sınıf Vektörler Testleri Çöz
11. sınıf Vektörler Ders Notu
Fizik bilimi, doğadaki olayları incelerken gözlem yapar. Yaptığı gözlemleri de anlaşılır bir dille ifade eder. Örneğin bir aracın 100 km/h hızla hareket ettiğini gözleyen bir bilim insanı, aracın hareketi ile ilgili bilgi verirken hareket yönünü de belirtir. Çünkü kuzeye doğru 100 km/h hızla giden bir aracın hareketi ile bir çember üzerinde 100 km/h büyüklükteki hızla (süratle) giden bir aracın hareketi aynı değildir.
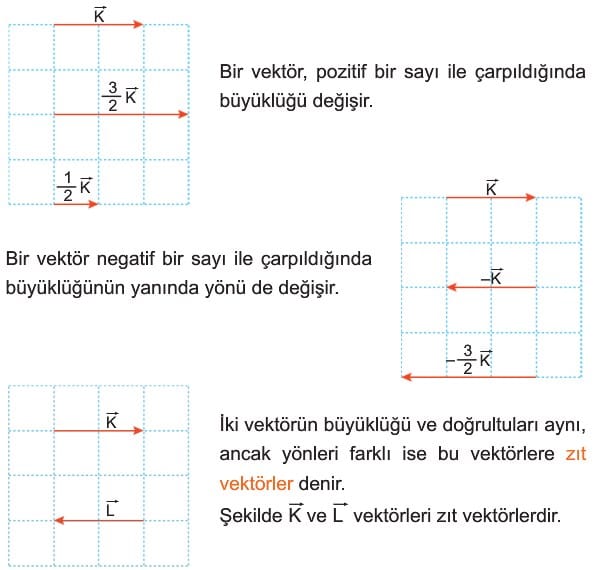
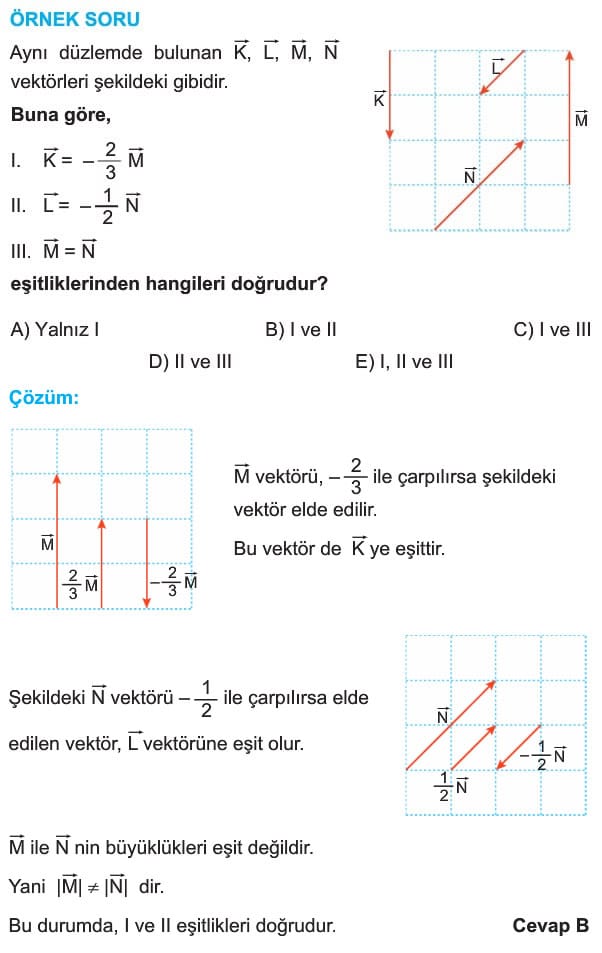
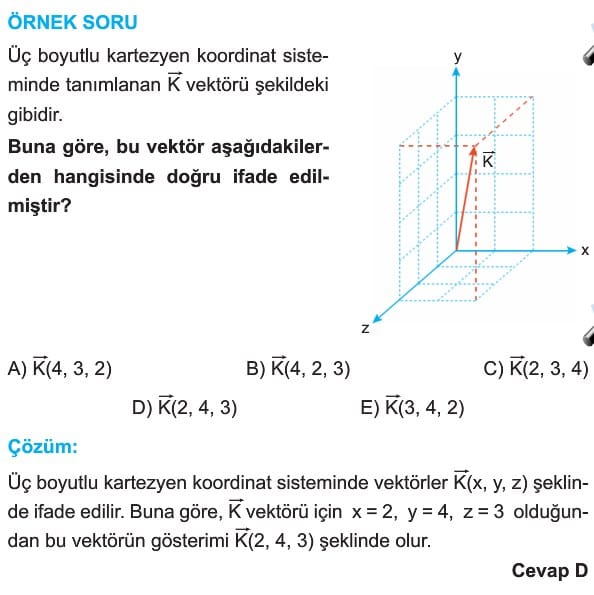
Hız gibi yönü ile ifade edilen büyüklüklere vektörel büyüklükler denir. Vektörel büyüklük, temsil edildiği doğrultuda, uzunluğu vektörel niceliğin şiddeti ile orantılı bir ok çizilerek gösterilir. Bu şekilde yönü ve büyüklüğü belirtilerek çizilen oka vektör denir.
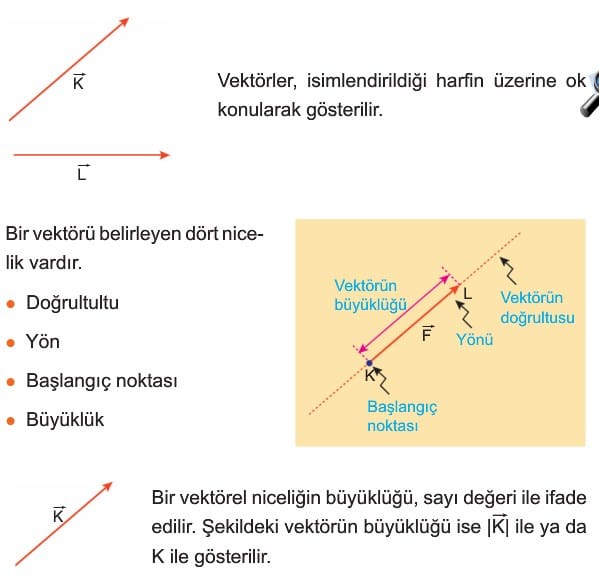

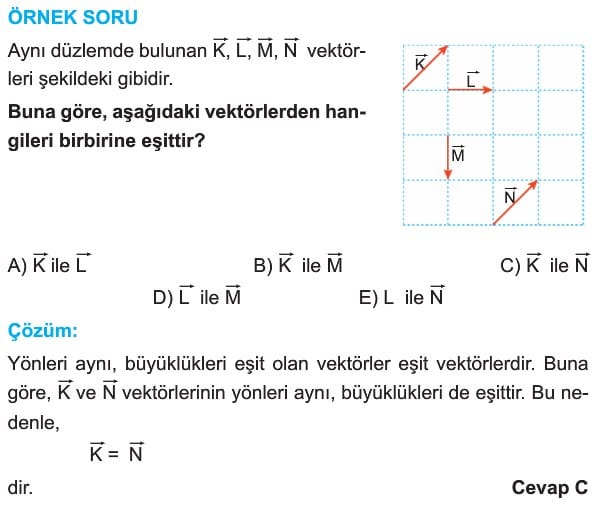


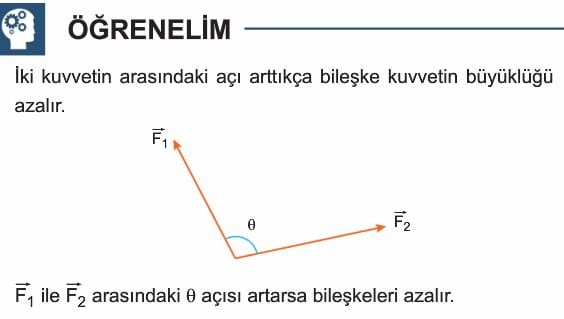
BİLEŞKE VEKTÖR
Aynı türden iki ya da daha fazla skaler büyüklüğü toplamak için basit aritmetik kullanılır. Bir sepette bulunan 3 kg elma üzerine 4 kg daha elma konulursa sepetteki elmanın kütlesi 7 kg olur. Halbuki 3 m kuzeye, 4 m doğuya yürüyen bir çocuk 7 m yürümesine rağmen hareket noktasından itibaren 7 m yer değiştirme yapmamıştır. Çocuğun gerçek yer değiştirmesi, vektörel toplama ile bulunur.
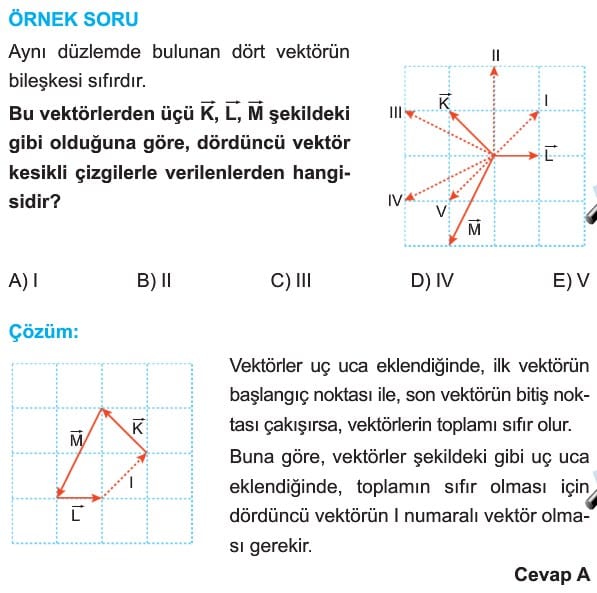
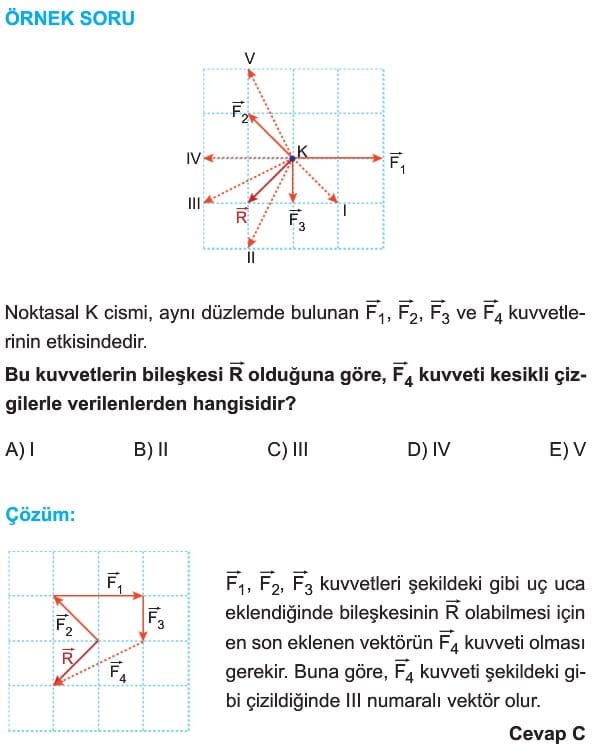
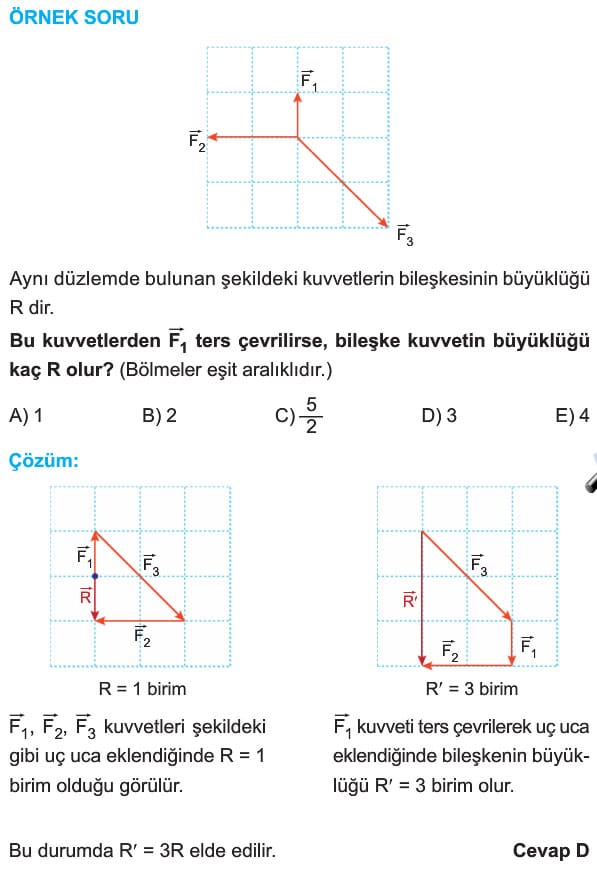
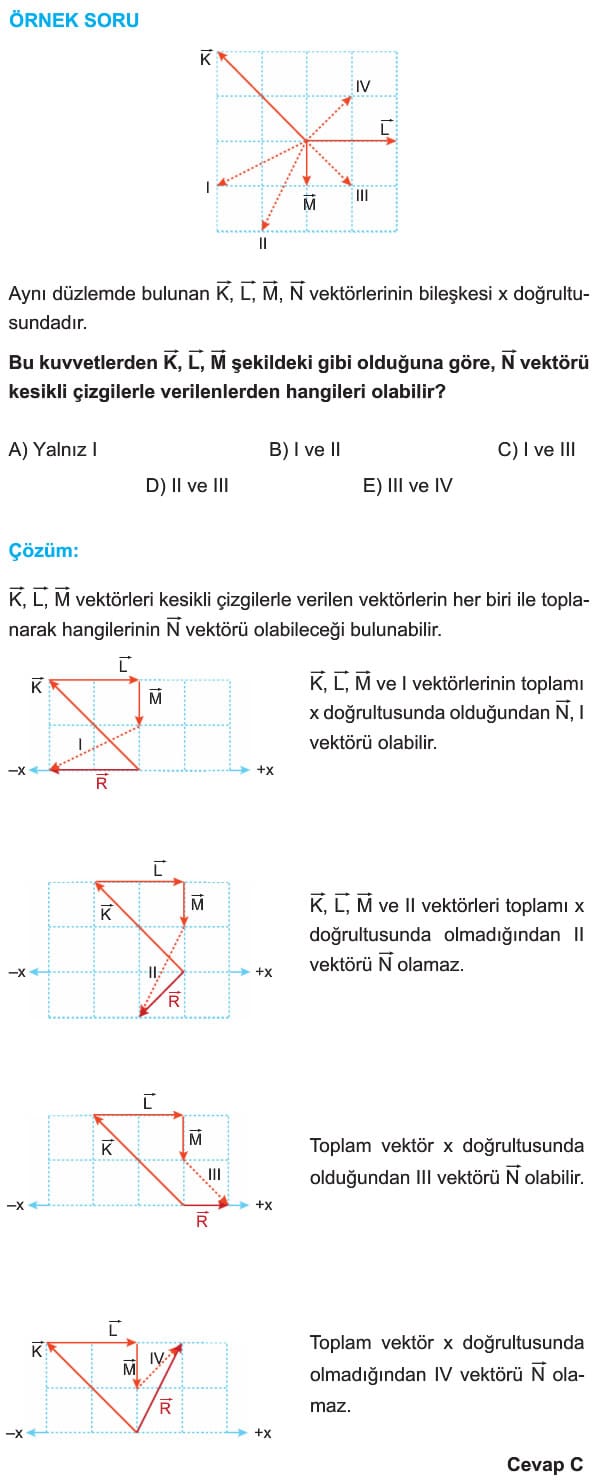
İki ya da daha fazla vektörün toplanmasıyla elde edilen vektöre bileşke vektör denir. Bileşke vektör genelde R harfi ile gösterilir. Vektörlerin bileşkesi bulunurken genellikle iki yöntem kullanılır.
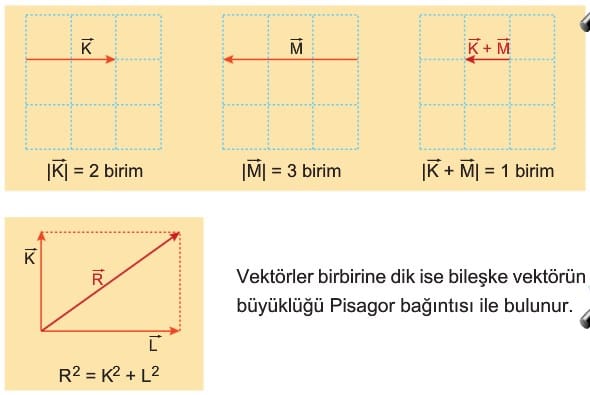
Uç Uca Ekleme Yöntemi
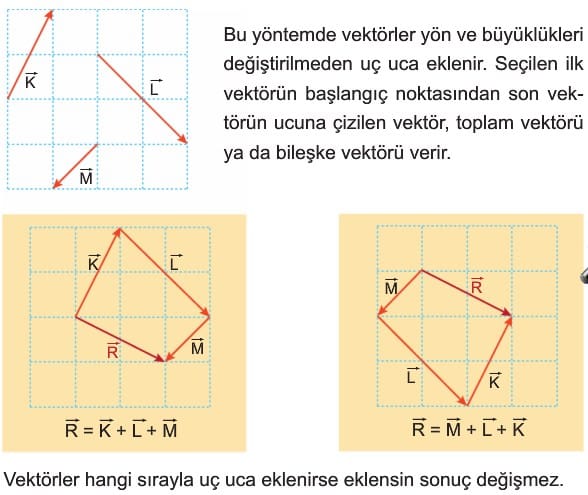
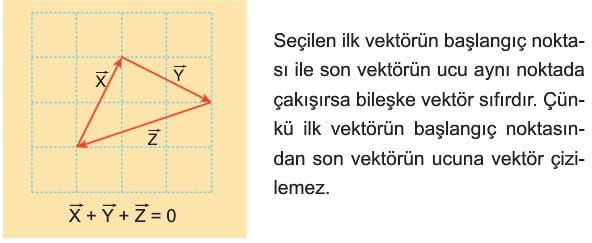
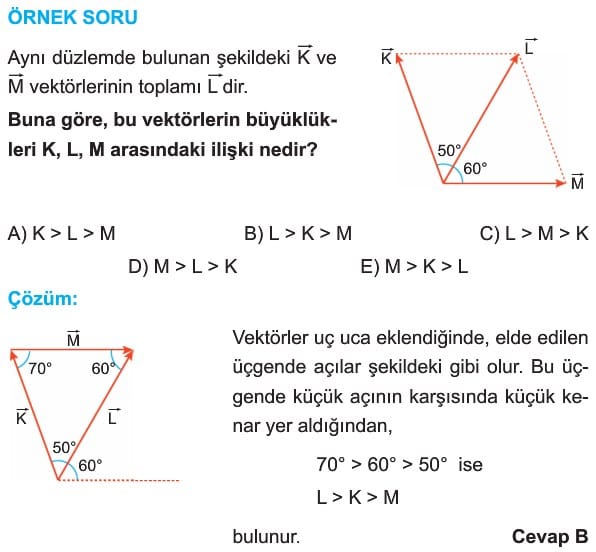
Çözümlü Sorular
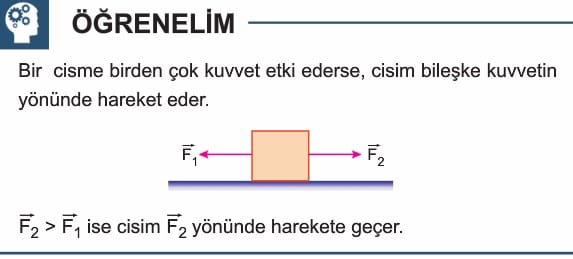
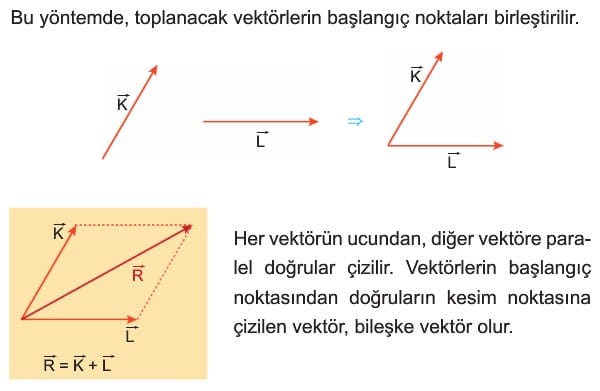
Paralelkenar Yöntemi


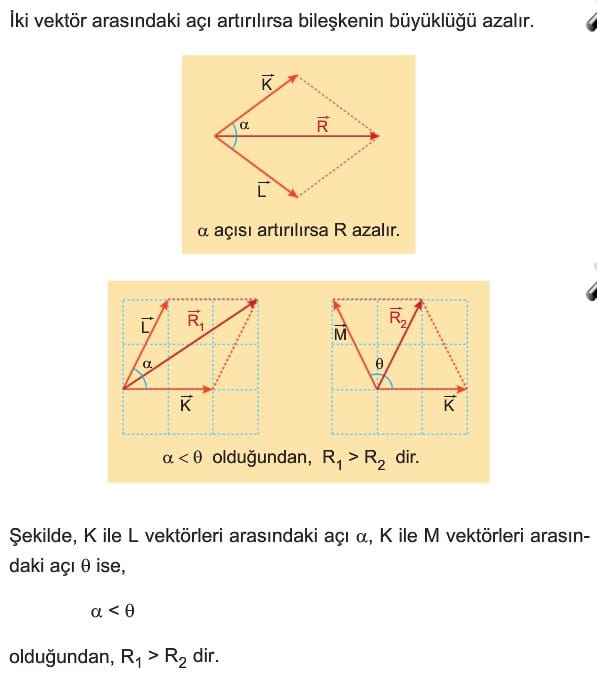
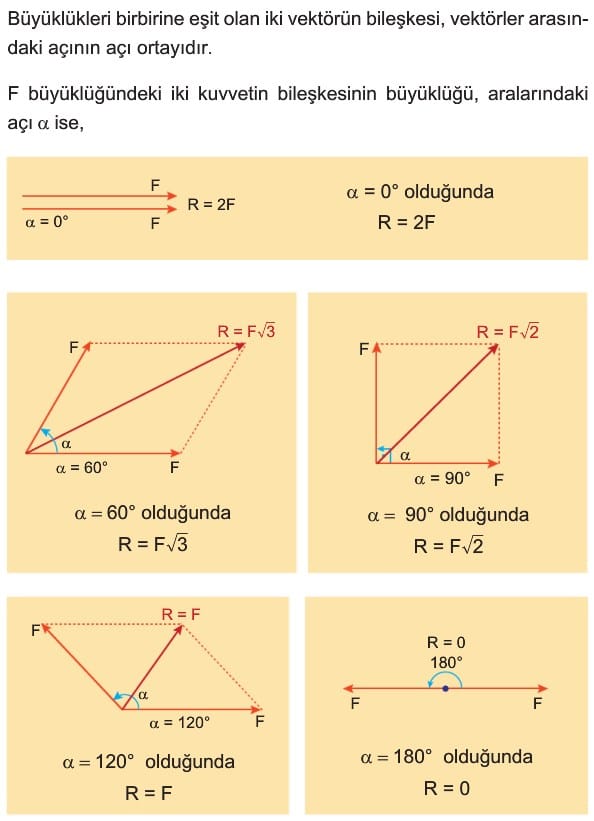
Bileşke Vektörün Özellikleri
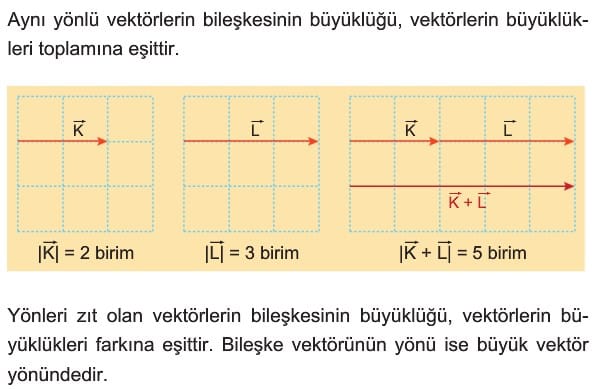




Çözümlü Sorular

Çözümlü Sorular
Vektörlerde Çıkarma İşlemi

Çözümlü Sorular
Vektörlerin Bileşenlerine Ayrılması
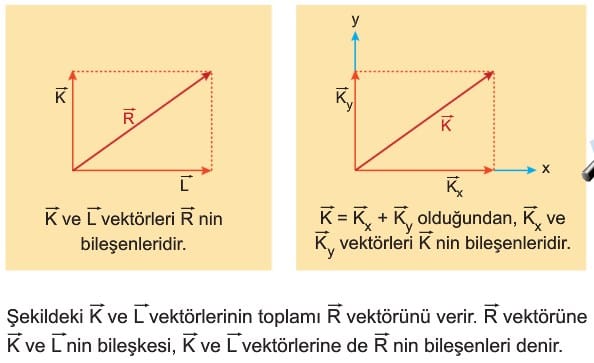
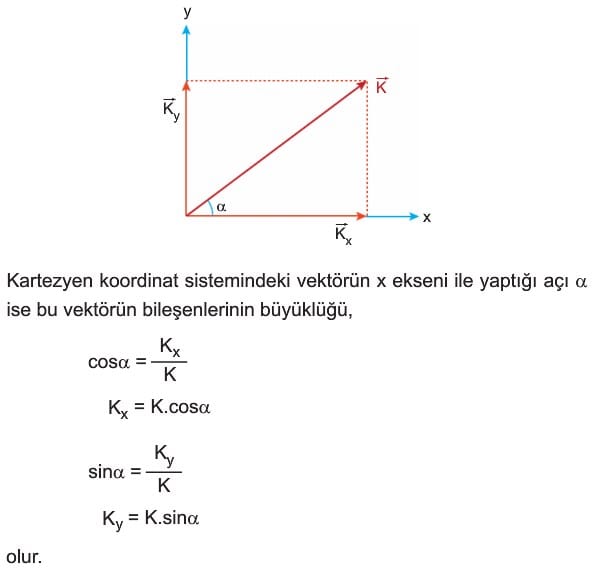
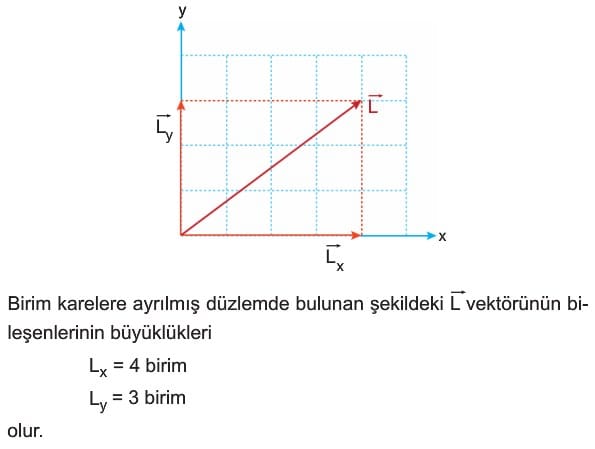
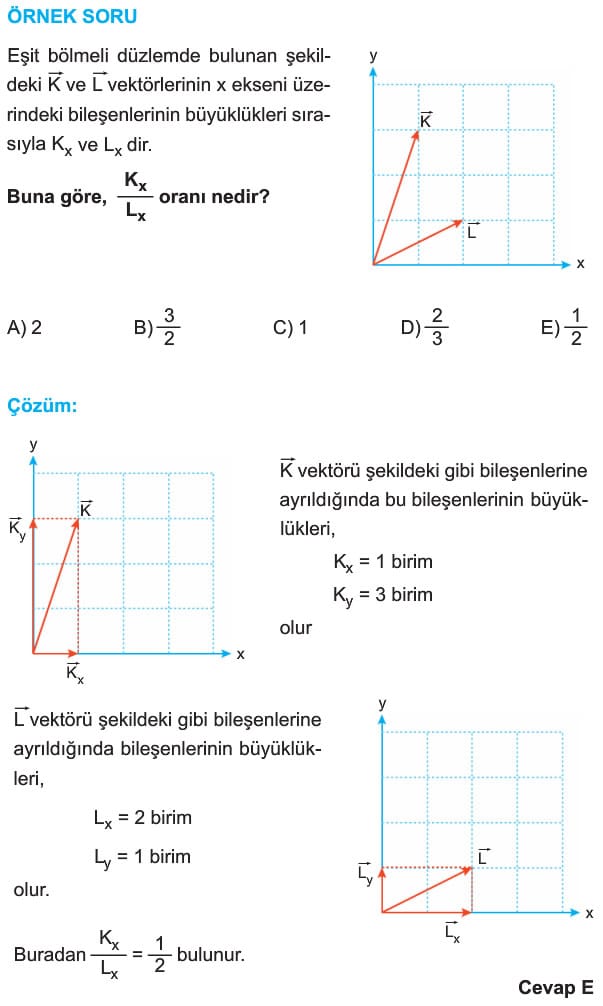
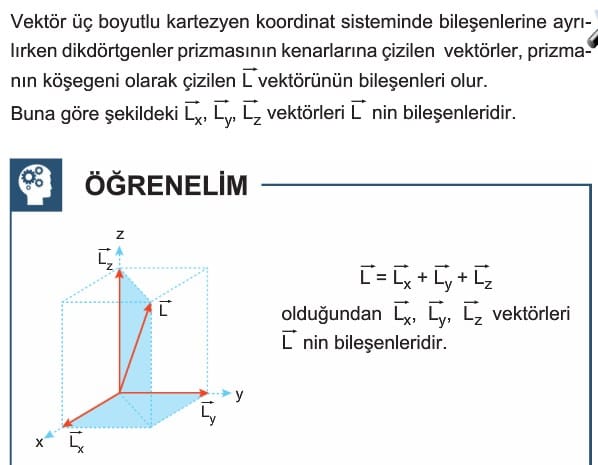
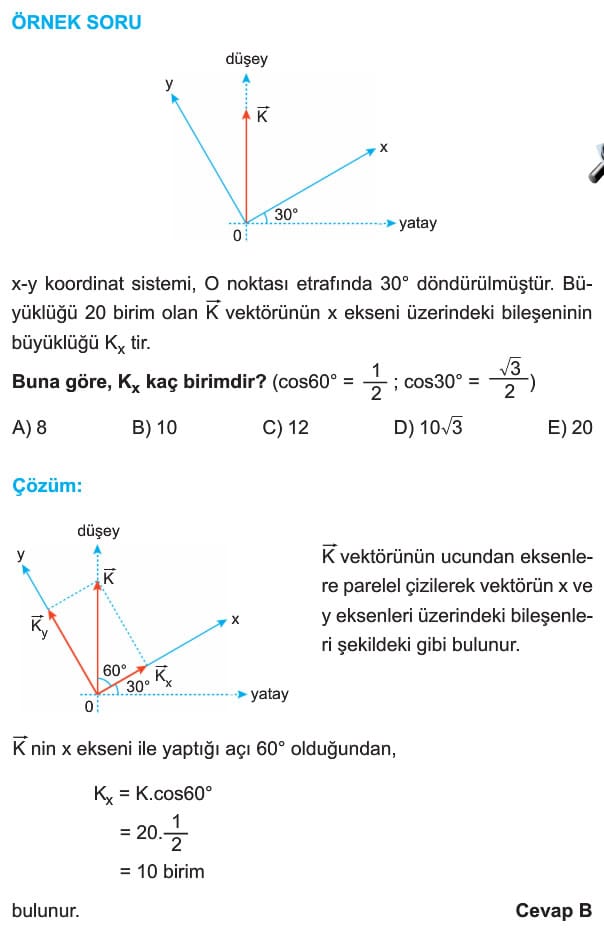
Bir vektör iki boyutlu kartezyen koordinat sisteminde bileşenlerine ayrılırken vektörün ucundan eksenlere paralel çizilir. Vektörün başlangıç noktasından eksenlerin kesildiği noktaya çizilen vektörler, dik bileşenler olarak adlandırılır. İki boyutlu kartezyen koordinat sisteminde, bileşenlerin büyüklükleri trigonometrik tanımlardan yararlanarak bulunabilir.

11. Sınıf Kuvvet ve Hareket Konuları
- Vektörler
- Bağıl Hareket
- Newton’ın Hareket Yasaları
- Bir Boyutta Sabit İvmeli Hareket
- İki Boyutta Hareket
- Enerji ve Hareket
- İtme ve Çizgisel Momentum
- Tork
- Denge ve Denge Şartları
- Basit Makineler
Kısa Konu Özeti
1. Vektör Tanımı
Vektörler, bir büyüklük ve bir yön içeren fiziksel niceliklerdir. Örnek olarak kuvvet, hız ve ivme vektörlerdir. Vektörler, genellikle oklarla gösterilir. Okun uzunluğu, vektörün büyüklüğünü; okun yönü ise vektörün yönünü belirtir.
2. Vektör Büyüklüğü
Vektörün büyüklüğü, genellikle bir pozitif sayı ile ifade edilir ve vektörün boyutu veya kuvveti hakkında bilgi verir. Bir vektör A için büyüklüğü |A| ile gösterilir.
3. Vektör Bileşenleri
Her vektör, bileşenlerine ayrılabilir. Düzlemdeki bir vektör iki bileşenden oluşur:
- Yatay Bileşen (Ax): Ax = |A| * cos(θ)
- Dikey Bileşen (Ay): Ay = |A| * sin(θ)
Burada θ, vektörün yatay eksenle yaptığı açıdır.
4. Vektör Toplama
Vektörler, birleştirilerek toplam vektör oluşturulabilir. İki vektör A ve B için toplam vektör C şu şekilde bulunur:
- Grafiksel Yöntem: Vektörleri baştan uca yerleştirerek toplam vektör çizilir.
- Analitik Yöntem: Vektörlerin bileşenleri toplanarak elde edilir:
Cx = Ax + Bx
Cy = Ay + By
5. Vektör Çıkarma
Vektör çıkarma, bir vektörün diğerine eklenmesi ile yapılır. A – B işlemi, A + (-B) şeklinde ifade edilebilir.
6. Vektörlerin Çarpımı
Vektörler arasında iki tür çarpma işlemi vardır:
- Skalar Çarpım (Dot Product): İki vektörün skalar çarpımı, iki vektörün büyüklüklerinin çarpımının, aralarındaki açının kosinüsüne eşittir.
- Vektörel Çarpım (Cross Product): İki vektörün vektörel çarpımı, yeni bir vektör oluşturur ve bu vektör, orijinal vektörlere dik olacak şekilde yönlendirilir.
7. Vektörlerin Kullanım Alanları
Vektörler, fiziksel olayların modellenmesinde önemli bir rol oynar. Örneğin:
- Kuvvetler: Bir cismi etkileyen kuvvetlerin yönleri ve büyüklükleri.
- Hız: Bir cismin hareket yönü ve hızı.
- İvme: Cisimlerin hız değişim oranları.
8. Vektörler ve Fiziksel Problemler
Vektörler, fiziksel problemlerde doğru sonuçlar elde etmek için kullanılır. Vektörlerin analitik ve grafiksel çözümleri, fiziksel olayların daha iyi anlaşılmasını sağlar.
Çözümlü Örnek Test Soruları
Vektörler, hem büyüklüğü hem de yönü olan fiziksel niceliklerdir. Vektörlerin büyüklüğü ve yönü olduğu için vektörlerle işlemler yaparken özel kurallar uygulanır. Vektörlerin bileşenlerine ayrılması, toplanması ve çıkarılması gibi işlemler fizik problemlerinin çözümünde önemlidir.
1. Bir vektörün büyüklüğü neyi ifade eder?
A) Vektörün yönünü
B) Vektörün doğrultusunu
C) Vektörün şiddetini veya uzunluğunu
D) Vektörün başlangıç noktasını
Çözüm: Vektörün büyüklüğü, vektörün şiddetini veya uzunluğunu ifade eder.
Doğru cevap C şıkkıdır.
2. Aşağıdaki niceliklerden hangisi bir vektör büyüklüğüdür?
A) Kütle
B) Hız
C) Sıcaklık
D) Enerji
Çözüm: Hız, yönü ve büyüklüğü olan bir vektör büyüklüğüdür.
Doğru cevap B şıkkıdır.
3. İki vektörün toplamı olan bileşke vektör nasıl bulunur?
A) Vektörler toplanırken sadece büyüklükleri toplanır
B) Vektörler skaler olarak çarpılır
C) Vektörler başlangıçtan son noktaya birleştirilir
D) Vektörler ayrı ayrı yönlere bölünür
Çözüm: İki vektörün toplamı, başlangıç noktası birleştirilerek vektörlerin uç uca eklenmesiyle bulunur.
Doğru cevap C şıkkıdır.
4. Bir vektörü bileşenlerine ayırmak ne anlama gelir?
A) Vektörün büyüklüğünü azaltmak
B) Vektörü yatay ve düşey yönlere bölmek
C) Vektörün yönünü değiştirmek
D) Vektörü sadece büyüklüğüne indirgeyerek basitleştirmek
Çözüm: Vektörü bileşenlerine ayırmak, onu yatay ve düşey yönlerdeki vektörlere bölmeyi ifade eder.
Doğru cevap B şıkkıdır.
5. Aşağıdaki işlemlerden hangisi vektörlerle yapılabilen bir işlemdir?
A) Vektörlerin frekansını bulmak
B) Vektörlerin büyüklüğünü toplamak
C) Vektörlerin bileşenlerini toplamak
D) Vektörlerin yansımasını bulmak
Çözüm: Vektörlerin bileşenleri ayrı ayrı toplanarak toplam vektör bulunabilir.
Doğru cevap C şıkkıdır.
6. İki zıt yönlü vektörün toplamı nasıl bulunur?
A) Büyüklükleri toplanır
B) Büyüklükleri çıkarılır, büyük olandan küçük olan çıkarılır
C) Büyüklükleri çarpılır
D) Büyüklükleri aynı yönde olduğu için değişmez
Çözüm: İki zıt yönlü vektörün toplamı, büyüklüklerinin çıkarılmasıyla bulunur. Büyük olandan küçük olan çıkarılır ve yön büyük olanın yönü olur.
Doğru cevap B şıkkıdır.
7. Aşağıdaki vektör işlemlerinden hangisi doğrudur?
A) İki vektörün toplamı her zaman sıfırdır
B) Bir vektörün bir skalerle çarpılması vektörün yönünü değiştirir
C) Vektörlerin bileşkesi her zaman bir büyüklük verir
D) Vektörlerin yönü büyüklüklerinden bağımsızdır
Çözüm: Vektörlerin bileşkesi bir büyüklük ve yönü olan yeni bir vektördür.
Doğru cevap C şıkkıdır.
8. Aynı büyüklüğe ve zıt yönlere sahip iki vektörün toplamı nedir?
A) Sıfır
B) İki katı
C) Yönü ters olan bir vektör
D) Büyüklükleri çarpılmış bir vektör
Çözüm: Aynı büyüklüğe ve zıt yönlere sahip iki vektör birbirini götürür ve toplamları sıfır olur.
Doğru cevap A şıkkıdır.
Çözümlü Örnek Sorular: Vektörler
Soru 1:
Bir vektörün bileşenleri Vx = 3 N ve Vy = 4 N olarak verilmiştir. Bu vektörün büyüklüğü kaç N’dir?
A) 5 N
B) 7 N
C) 9 N
D) 12 N
Çözüm:
Bir vektörün büyüklüğü, bileşenlerinin karelerinin toplamının karekökü ile bulunur. Bu durumda:
V = √(Vx² + Vy²)
V = √(3² + 4²)
V = √(9 + 16)
V = √25 = 5 N
Cevap: A) 5 N
Soru 2:
İki vektörün büyüklükleri 6 N ve 8 N olup, aralarındaki açı 90°’dir. Bu iki vektörün bileşke vektörünün büyüklüğü kaç N’dir?
A) 8 N
B) 10 N
C) 12 N
D) 14 N
Çözüm:
İki vektör arasındaki açı 90° ise, bileşke vektör Pisagor teoremi ile bulunur:
R = √(6² + 8²)
R = √(36 + 64)
R = √100
R = 10 N
Cevap: B) 10 N
Soru 3:
Bir cismin hızı, 30°’lik bir açı ile 20 m/s hız vektörü ile gösteriliyor. Bu hızın yatay bileşeni kaç m/s’dir?
A) 10 m/s
B) 15 m/s
C) 17.32 m/s
D) 20 m/s
Çözüm:
Yatay bileşen, hızın cosinüs bileşeni ile hesaplanır:
Vx = V * cosθ
Vx = 20 * cos30°
Vx = 20 * (√3 / 2)
Vx ≈ 17.32 m/s
Cevap: C) 17.32 m/s
Soru 4:
İki vektörün büyüklükleri sırasıyla 5 N ve 12 N’dir. Bu iki vektör zıt yönlerde ise bileşke vektörün büyüklüğü kaç N olur?
A) 7 N
B) 17 N
C) 5 N
D) 12 N
Çözüm:
Zıt yönlü vektörler çıkarılarak bileşke vektör bulunur:
R = |12 – 5| = 7 N
Cevap: A) 7 N
Soru 5:
Bir cismin hız vektörü 10 m/s olup, yatayla 60° açı yapmaktadır. Bu hızın dikey bileşeni nedir?
A) 5 m/s
B) 8.66 m/s
C) 10 m/s
D) 12 m/s
Çözüm:
Dikey bileşen, hızın sinüs bileşeni ile hesaplanır:
Vy = V * sinθ
Vy = 10 * sin60°
Vy = 10 * (√3 / 2)
Vy ≈ 8.66 m/s
Cevap: B) 8.66 m/s
Soru 6:
Aynı doğrultudaki iki vektörden biri 10 N, diğeri ise 15 N büyüklüğündedir. Bu vektörlerin bileşkesi nedir?
A) 5 N
B) 10 N
C) 15 N
D) 25 N
Çözüm:
Aynı doğrultudaki vektörler toplanarak bileşke bulunur:
R = 10 + 15 = 25 N
Cevap: D) 25 N
Soru 7:
Bir vektörün bileşenleri Vx = 7 N ve Vy = 24 N olarak verilmiştir. Bu vektörün büyüklüğü kaç N’dir?
A) 25 N
B) 31 N
C) 17 N
D) 12 N
Çözüm:
Vektörün büyüklüğü Pisagor teoremi ile bulunur:
V = √(7² + 24²)
V = √(49 + 576)
V = √625 = 25 N
Cevap: A) 25 N
Soru 8:
Bir vektör, 45° açıyla 10 N büyüklüğünde bir kuvvetle uygulanıyor. Bu vektörün yatay ve dikey bileşenlerinin büyüklükleri nedir?
A) 5√2 N
B) 5 N
C) 7.07 N
D) 10 N
Çözüm:
Vektörün yatay ve dikey bileşenleri cos45° ve sin45° ile bulunur:
Vx = 10 * cos45° = 10 * (√2 / 2) ≈ 7.07 N
Vy = 10 * sin45° = 10 * (√2 / 2) ≈ 7.07 N
Cevap: C) 7.07 N