Üslü İfadeler 8. Sınıf Lgs Matematik
8. Sınıf Lgs Üslü İfadeler Testleri
8. SINIF LGS ÜSLÜ İFADELER DERS NOTU
a bir sayı, n bir pozitif tam sayı olmak üzere; n tane a sayısının çarpımı aⁿ ile gösterilir.
a: Taban
n: Kuvvet (Üs)
Örnek: 3⁶ = 3 × 3 × 3 × 3 × 3 × 3
- Taban = 3
- Üs = 6
3⁶ sayısı “üç üssü altı” diye okunur.
Önemli Bilgi:
– Sıfırdan farklı bir sayının sıfırıncı kuvveti daima 1’dir. (a ≠ 0 ise a0 = 1’dir)
– Herhangi bir sayının 1. kuvveti her zaman sayının kendisine eşittir. (a1 = a’dır.)
– 1’in tüm kuvvetleri 1’e eşittir (1m = 1)
Örnek Soru: 4³ + 3⁰ + 2⁵ – 9¹ işleminin eşitini bulalım.
Çözüm: 4³ = 4 × 4 × 4 = 64
3⁰ = 1
2⁵ = 2 × 2 × 2 × 2 × 2 = 32
9¹ = 9
Öyleyse, 4³ + 3⁰ + 2⁵ – 9¹ işlemi:
64 + 1 + 32 – 9 = 88 bulunur.
Önemli Bilgi: Pozitif bir sayının tüm kuvvetleri pozitiftir.
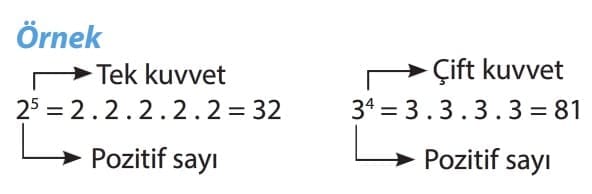
Önemli Bilgi:Negatif bir sayının çift kuvvetleri pozitif, tek kuvvetleri ise negatiftir.
(-)çift = +
(-)tek = –
Örnek:
(-2)⁴ = (-2) × (-2) × (-2) × (-2) = 16
Taban Negatif sayı ve kuvvet çift → Sonuç pozitif
(-2)⁵ = (-2) × (-2) × (-2) × (-2) × (-2) = -32
Taban Negatif sayı ve kuvvet tek → Sonuç negatif
Dikkat: Üslü bir ifadede taban negatif ise işaret incelemesi yapıldıktan sonra işlemlere devam edilmesi kolaylık sağlar. Taban negatif ise kuvvetin yeri önemlidir. Negatif sayılarda çift kuvvet parantezin dışında ise sonuç pozitiftir.
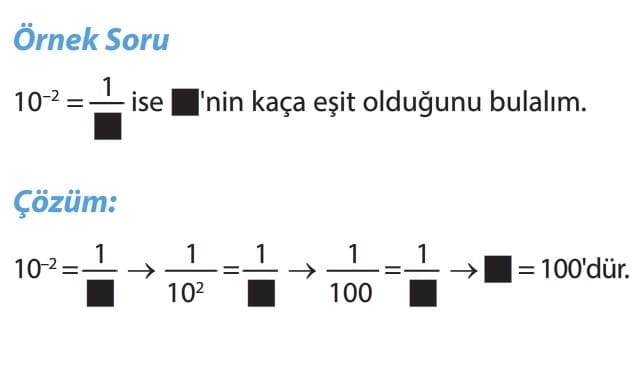
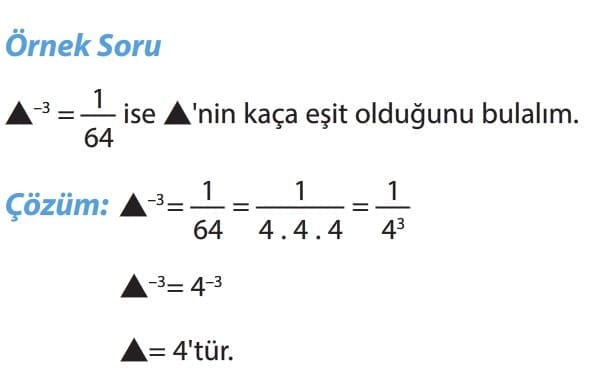
A. NEGATİF ÜS

Dikkat: Üslü bir sayının önündeki “-” işareti ile kuvvetinde bulunan “-” işaretlere dikkat etmek gerekir. Üslü sayının önündeki “-” işaret sayıyı negatif yaparken üslü sayının kuvvetindeki “-” işareti sayının pay ve paydasında yerlerini değiştirir.


B. ONDALIK GÖSTERİMLERİN VE RASYONEL SAYILARIN KUVVETLERİ
Ondalık gösterimlerin veya rasyonel sayıların tekrarlı çarpımlarının üslü bir eşitini bulurken tekrarlanan sayıları tabana, kaç kez çarpılıyorsa bu sayıyı da tabanın üssüne yazarız.
Dikkat: Ondalıklı bir kesrin kuvvetinin değerini bulurken öncelikle ondalıklı sayıyı rasyonel sayıya çevirip ardından sadeleştirilebiliyorsa sadeleştirip sonuca gitmek işlem kolaylığı sağlar.
C. ÜSLÜ İFADENİN ÜSSÜ
- Üslü bir ifadenin tekrar üssü alınırsa üsler çarpılır.
( ab ) c = a b.c
Dikkat: Üslü ifadelerle ilgili hesaplamalarda tabandaki sayının üslü yazılması işlem kolaylığı sağlar.
D. ÜSLÜ DENKLEMLER
a ≠ 0, a ≠ 1, a ≠ -1 olmak üzere;
ise
x = y’dir.Tabanları eşit olan üslü ifadelerin üssü de birbirine eşittir.
E. ÜSLÜ İFADELERDE SIRALAMA
- 1’den büyük üslü sayılarda sıralama yapılırken tabanlar eşitse üssü küçük olan daha küçüktür.
Örnek Soru: x = 10⁵, y = 10³ ve z = 10⁷’dir.
Buna göre, x, y ve z ifadelerini büyükten küçüğe doğru sıralayalım.
Çözüm: x= 10⁵, y = 10³ ve z = 10⁷ ifadelerinde tabanlar eşit olduğundan, üssü büyük olan daha büyüktür.
Buna göre: z > x > y olur.
107 > 105 > 103
- 1’den büyük üslü sayılarda sıralama yapılırken üsler eşitse tabanı küçük olan daha küçüktür.
Örnek Soru: 7³, 5³, 3³, 2³ sayılarını küçükten büyüğe doğru sıralayalım.
Çözüm: Üsleri eşit olan sayılarda tabanı küçük olan daha küçük olur.
Buna göre:
2³ < 3³ < 5³ < 7³ olur.
Dikkat: Üsleri veya tabanları aynı olmayan sayıları sıralamak için, verilen üslü sayıların tabanlarını üslü yazarak tabanı veya üssü aynı yapmaya çalışınız.
F. ÜSLÜ İFADELERDE İŞLEMLER
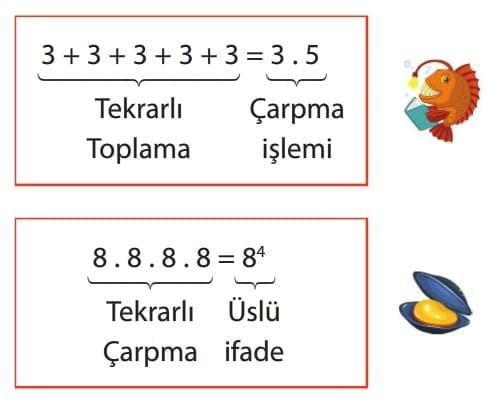
Tekrarlı toplama, kısaca çarpma işlemi şeklinde ve tekrarlı çarpma ise kısaca üslü ifade şeklinde gösterilebilir.
G. ÜSLÜ İFADELERDE ÇARPMA İŞLEMİ
Tabanları aynı olan üslü ifadeleri çarpmak için, üsler toplanır ve ortak tabana üs olarak yazılır.
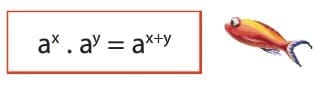
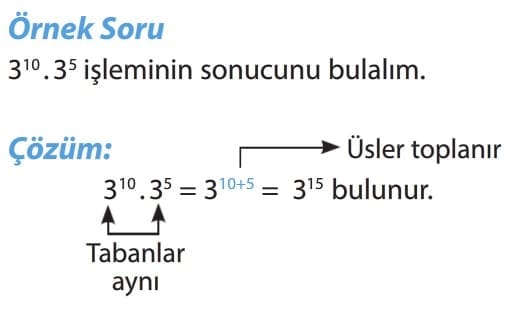
Dikkat: Tabanları ve üsleri farklı olan üslü ifadelerin çarpımında tabandaki sayılar üslü şekilde yazılır ve tabanlar aynı yapılmaya çalışılır.

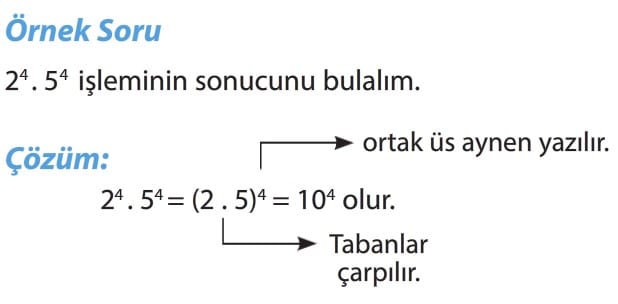
Dikkat: Üsleri aynı olan ifadelerin çarpımında, tabanlar çarpılır ve ortak üs aynen yazılır.
ax . bx = (a . b)x
Dikkat: Üslü ifadelerin çarpımında tabanlar veya üsler aynı yapılamıyorsa her bir üslü ifadenin değeri bulunup çarpılır.
Dikkat: Parantez içinde çarpım şeklinde bulunan sayıların kuvveti alınırken parantez İçindeki her bir sayının kuvveti ayrı ayrı alınır.
(a . b)n= an. bn
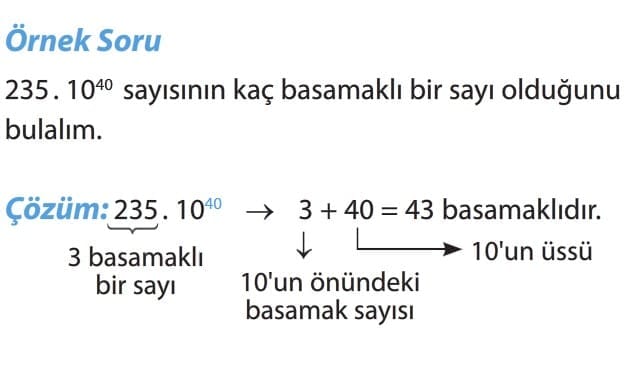
Bilgi: a . 10n şeklinde bir sayının basamak sayısı bulunurken 10’un üssü ile önündeki sayının basamak sayısı toplanır.
Bilgi: a bir tam sayı olmak üzere a . 10n şeklinde bir sayının sondan sıfır olan basamak sayısı 10’un kuvvetine eşittir.
H. ÜSLÜ İFADELERDE BÖLME
Tabanları aynı olan üslü ifadeler ile bölme işlemi yapılırken ortak taban bölüme taban olarak yazılır. Payın üssünden paydanın üssü çıkarılarak ortak tabana üs olarak yazılır.
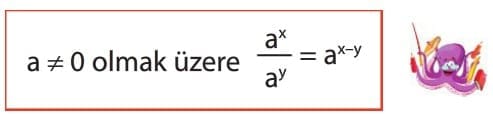
Bilgi: Üsleri aynı olan ifadelerin bölümünde, tabanlar bölünür; ortak üs bölüme üs olarak yazılır.

Dikkat: Bir üslü ifadenin başka bir üslü ifadenin kaç katı olduğu bulunurken diğer ifade katı sorgulanan ifadeye bölünür.

I. ONDALIK GÖSTERİMLERİN ÇÖZÜMLENMESİ
Bir ondalık gösterimin çözümlenmesinde ondalık sayının rakamları basamak değerlerinin toplamı şeklinde yazılır. Ondalık gösterimlerin çözümlenmesi kesirlerin 10’un kuvvetleri şeklinde yazılmasıyla da yapılabilir.
J. ÇOK BÜYÜK VE ÇOK KÜÇÜK SAYILAR
Çok büyük ve çok küçük sayıların üslü gösteriminde 10’un pozitif ve negatif tam sayı kuvvetlerinden faydalanılır.
1. 10’un Pozitif Tam Sayı Kuvvetleri

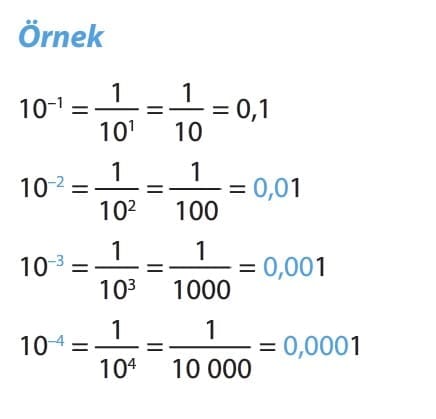
2. 10’un Negatif Tam Sayı Kuvvetleri
Dikkat: Bir ondalık gösterimi 10, 100, 1000 gibi 10’un kuvvetleri ile kısa yoldan çarpmak için ondalık gösterimin virgülü, 10’un kuvvetindeki sıfırların sayısı kadar sağa doğru kaydırılır. Eksik basamak varsa sıfır yazılarak tamamlanır.

Dikkat: Bir ondalık gösterimi 10, 100, 1000 gibi 10’un kuvvetleri ile kısa yoldan bölmek için ondalık gösterimin virgülü, 10’un kuvvetindeki sıfır sayısı kadar sola doğru kaydırılır. Eksik basamak varsa sıfır yazılarak tamamlanır.

Dikkat: a,bcd . 10n ifadesinde virgül sağa kayarken her basamak için n, 1 azalır ve virgül sola kayarken her basamak için n 1 artar.

K. BİLİMSEL GÖSTERİM
a bir gerçek sayı 1 ≤ |a| < 10 ve n tam sayı olmak üzere, a . 10n şeklindeki ifadelere bilimsel gösterim denir.
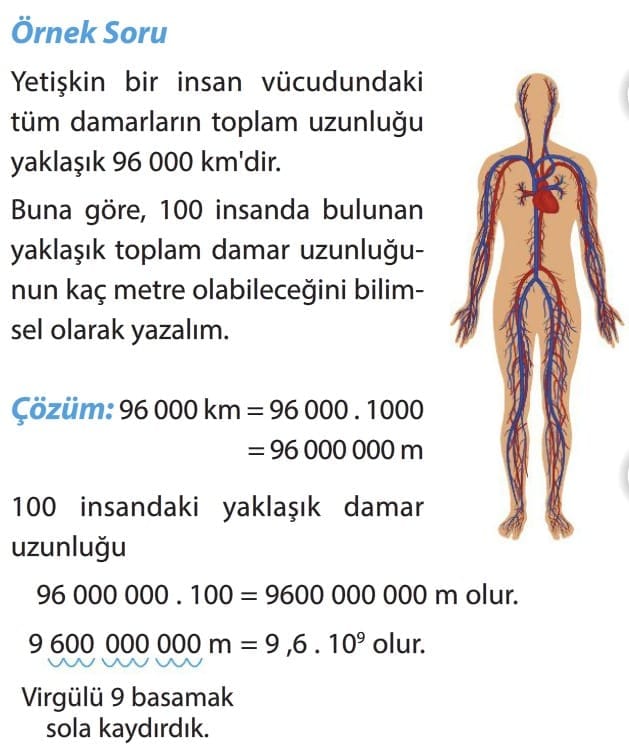
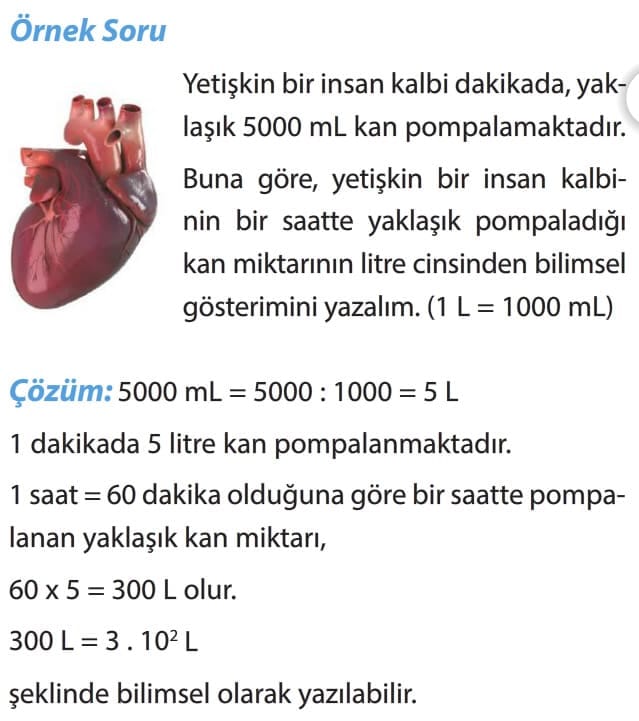
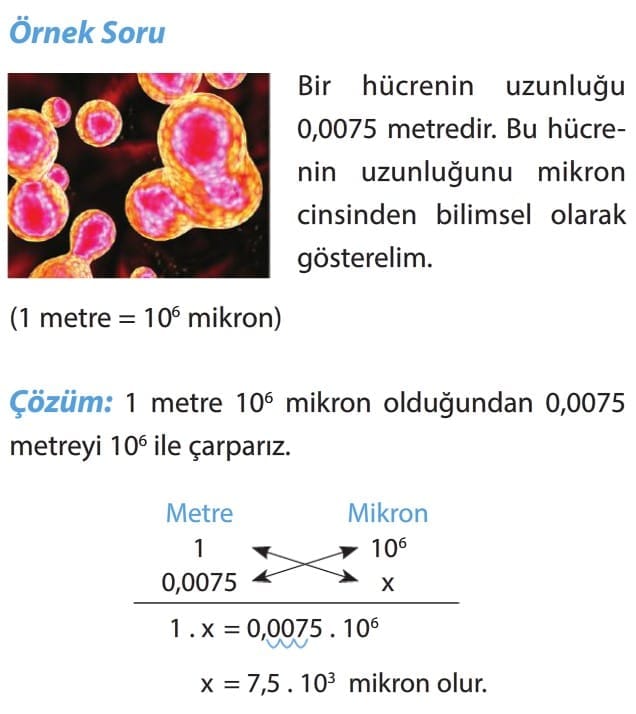
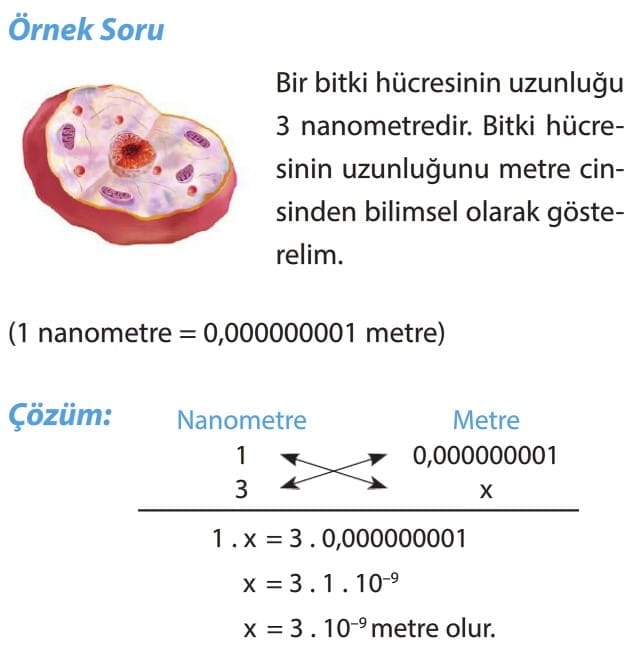
Dikkat: Bilimsel gösterimle ilgili problemlerde soruların sonunda bilimsel gösterimin hangi birim cinsinden istenildiğine dikkat ediniz.
Soru 1:
Üslü Sayılarla Çarpma
2⁴ × 2³ işleminin sonucunu bulunuz.
Çözüm: Aynı tabana sahip üslü sayılar çarpılırken üsler toplanır. Yani:
- 2⁴ × 2³ = 2⁷
Şimdi 2⁷’yi hesaplayalım:
- 2⁷ = 2 × 2 × 2 × 2 × 2 × 2 × 2 = 128
Soru 2:
Üslü Sayılarla Bölme
6⁵ ÷ 6² işleminin sonucunu bulunuz.
Çözüm: Aynı tabana sahip üslü sayılar bölünürken üsler çıkarılır:
- 6⁵ ÷ 6² = 6³
Şimdi 6³’ü hesaplayalım:
- 6³ = 6 × 6 × 6 = 216
Soru 3:
Karmaşık Üslü İfade
3⁴ × 3⁻² ÷ 3⁻¹ işleminin sonucunu bulunuz.
Çözüm: İlk olarak çarpma ve bölme işlemlerini yapalım:
- 3⁴ × 3⁻² = 3² (çarpma işleminde üsler toplanır)
- 3² ÷ 3⁻¹ = 3³ (bölme işleminde üsler çıkarılır)
Şimdi 3³’ü hesaplayalım:
- 3³ = 3 × 3 × 3 = 27
Soru 4:
Birimlerle Üslü Sayılar
Bir bilgisayar dosyasının boyutu 3 gigabayttır. Bu dosyanın boyutunu bayt cinsinden bilimsel gösterimle yazınız. (1 gigabayt = 10⁹ bayt)
Çözüm: Bir gigabayt 10⁹ bayt olduğuna göre, 3 gigabayt şu şekilde yazılabilir:
- 3 × 10⁹ bayt
Soru 5:
Üslü Sayılarla Karşılaştırma
Aşağıdaki sayıları büyükten küçüğe sıralayınız:
- 5⁴, 3⁵, 2⁶
Çözüm: Her bir üslü ifadeyi hesaplayalım:
- 5⁴ = 625
- 3⁵ = 243
- 2⁶ = 64
Sıralama: 625 > 243 > 64
5⁴ > 3⁵ > 2⁶
Soru 6:
Negatif Üslü Sayılar
(-2)⁴ ve (-2)⁵ işlemlerinin sonuçlarını karşılaştırınız.
Çözüm: Negatif sayının çift kuvveti pozitif, tek kuvveti negatiftir.
- (-2)⁴ = 16 (pozitif)
- (-2)⁵ = -32 (negatif)
Sonuç: (-2)⁴ > (-2)⁵
Soru 7:
Bilimsel Gösterim
Bir laboratuvarda bakteri sayısı 4 × 10⁶ olarak tespit edilmiştir. Bakteri sayısının yarısı kaçtır? Bilimsel gösterimle yazınız.
Çözüm: Verilen sayı 4 × 10⁶’dır. Bakteri sayısının yarısını bulmak için bu sayıyı 2’ye böleriz:
- (4 × 10⁶) ÷ 2 = 2 × 10⁶
Soru 8:
Karmaşık Üslü Sayılar
(2³)⁴ ÷ (2²)⁵ işleminin sonucunu bulunuz.
Çözüm: İlk önce üslü sayıları çarpalım:
- (2³)⁴ = 2¹²
- (2²)⁵ = 2¹⁰
Sonra bölme işlemini yapalım:
- 2¹² ÷ 2¹⁰ = 2²
Şimdi 2²’yi hesaplayalım:
- 2² = 4