Üslü Gösterimlerle (Üslü Sayılarda) Toplama, Çıkarma, Çarpma ve Bölme İşlemi 9. Sınıf Matematik
Üslü sayılar, bir sayının kendisiyle belirli bir sayıda çarpılmasını ifade eden matematiksel bir gösterimdir ve bu gösterim, büyük veya küçük sayıları daha kolay ifade etmek için kullanılır. 9. sınıf matematik müfredatında üslü sayılarla yapılan toplama, çıkarma, çarpma ve bölme işlemleri üzerinde durulmaktadır. Çarpma işlemi yapılırken aynı tabana sahip üslü sayılarda üstler toplanır; bölme işlemi ise aynı tabana sahip üslü sayılarda üstlerin çıkarılmasını gerektirir. Toplama ve çıkarma işlemlerinde ise yalnızca aynı tabana ve aynı üslü sayılara sahip ifadeler bir araya getirilebilir. Bu konu, öğrencilere üslü sayılarla işlemler yaparken dikkat etmeleri gereken noktaları öğretirken, daha karmaşık matematiksel ifadelerin yönetilmesine de yardımcı olur. Üslü gösterim, birçok bilimsel hesaplamada kullanıldığından, günlük hayatta karşılaşılan problemleri çözme yeteneğini geliştirmede önemli bir rol oynar.
Gerçek Sayıların Üslü ve Köklü Gösterimleri ile Yapılan İşlemler Konuları
- Gerçek Sayıların Üslü Gösterimi
- Gerçek Sayıların Üslü Gösterimleriyle Yapılan Toplama, Çıkarma, Çarpma ve Bölme İşlemleri
- Üslü Gösterimleri Verilen Sayıların Üssünü Alma İşlemi
- Gerçek Sayıların Köklü Gösterimi ile Yapılan İşlemler
Üslü Gösterimler Online Testler ve Çözümlü Sorular
Üslü Gösterimlerle (Üslü Sayılarda) Dört İşlem (Toplama, Çıkarma, Çarpma ve Bölme) Ders Notu
Üslü Gösterimlerle (Üslü Sayılarda) Toplama ve Çıkarma İşlemi
Tabanları ve üsleri aynı olan ifadeler toplanırken, kat sayıların toplamı ile ortak olan üslü ifade çarpılır.
x.an + y.an = (x + y) . anTabanları ve üsleri aynı olan ifadeler çıkarılırken, kat sayıların farkı ile ortak olan üslü ifade çarpılır.
x.an – y.an = (x – y) . an
Çözümlü Sorular
Üslü Gösterimlerle (Üslü Sayılarda) Çarpma ve Bölme İşlemleri
Tabanları eşit olan üslü ifadelerin çarpımında; üsler toplanır ve elde edilen ifade ortak tabanın üssü olarak yazılır.
an . ap = an + pÜsleri eşit olan Üslü ifadelerin çarpımında, tabanlar çarpımı ortak üssün tabanı olarak yazılır.
xm . ym = (x . y)mTabanları eşit olan üslü ifadelerin bölümünde; paydaki sayının üssünden paydadaki sayının üssü çıkarılır ve elde edilen ifade ortak tabanın üstü olarak yazılır.
Üsleri eşit olan üslü ifadelerin bölümünü bulmak için; payın tabanı paydanın tabanına bölünür, ortak üs bölümün üssü olarak yazılır.


Üslü Gösterimlerle (Üslü Sayılarda) Çarpma ve Bölme İşlemleri Çözümlü Sorular
Üslü Gösterimlerle (Üslü Sayılarda) Toplama, Çıkarma, Çarpma ve Bölme İşlemi Video
Üslü Sayıların Tarihçesi:
Üslü sayılar, matematikte oldukça eski bir geçmişe sahiptir. Ancak, modern anlamda üslü sayılar ve üslü sayılarla ilgili temel kurallar, 17. yüzyılda matematikçi John Wallis tarafından geliştirilen çalışmalarla başlamıştır. Wallis, rasyonel sayılarla ifade edilemeyen kesirlerin çözümü için üslü notasyonu kullanmıştır.
Üslü sayılar ve üslü notasyon, daha sonra matematikçi Euler ve diğerleri tarafından daha da geliştirilmiştir. Bu notasyon, matematiksel ifadeleri daha kompakt ve güçlü bir şekilde ifade etmeye olanak tanımıştır.
Bugün, üslü sayılar temel matematiksel kavramlar arasında yer alır ve birçok matematik dalında yaygın olarak kullanılır. Üslü sayılar, özellikle cebir, analiz, fizik, mühendislik ve bilgisayar bilimleri gibi alanlarda önemli bir rol oynamaktadır.
Gerçek sayıların üslü gösterimleri, sayıları daha kompakt ve anlaşılır bir şekilde ifade etmeye yarar. Bu gösterimle yapılan çarpma ve bölme işlemleri, matematikte sıkça karşılaşılan problemlerin çözümünde temel bir rol oynar. Üslü sayılarla çarpma ve bölme işlemleri, bazı basit kurallara dayanır ve bu kurallar, işlemleri hızla ve doğru bir şekilde yapmayı mümkün kılar.
Çözümlü Örnek Test Soruları
Üslü sayılarla işlem yapmak, matematiksel hesaplamaların kolaylaştırılması için kullanılan önemli bir yöntemdir. Bu testte, üslü sayılarla toplama, çıkarma, çarpma ve bölme işlemlerini öğrenip pekiştireceksiniz. Üslü sayılarda işlemler, üslerin ve tabanların kuralları doğrultusunda yapılır.
Üslü Sayılarda Toplama ve Çıkarma İşlemi
1. 2³ + 2³ işleminin sonucu nedir?
a) 4³
b) 2⁶
c) 2⁴
d) 2 × 2³
Cevap: d) 2 × 2³
Çözüm: Üslü sayılarla toplama işlemi yapılırken, aynı tabanlı sayılar çarpan olarak alınır:
2³ + 2³ = 2 × 2³ = 2⁴.
2. 5² – 2 × 5² işleminin sonucu nedir?
a) 5²
b) 5³
c) -5²
d) -5² × 2
Cevap: c) -5²
Çözüm: Aynı tabanlı üslü sayılar arasında çıkarma işlemi yapılırken, ortak olan üslü sayı dışarı alınır:
5² – 2 × 5² = 1 × 5² – 2 × 5² = -5².
3. 3⁴ + 3³ işleminin sonucu nedir?
a) 3⁷
b) 3 × (3³ + 1)
c) 3³ × (3 + 1)
d) 3⁵
Cevap: c) 3³ × (3 + 1)
Çözüm: Farklı üslere sahip sayılar toplanırken, ortak çarpan olan küçük üs dışarı alınır:
3⁴ + 3³ = 3³ × (3 + 1) = 3³ × 4.
Üslü Sayılarda Çarpma İşlemi
1. 2² × 2⁵ işleminin sonucu nedir?
a) 2¹⁰
b) 2⁷
c) 4⁷
d) 2³
Cevap: b) 2⁷
Çözüm: Üslü sayılarda çarpma yapılırken tabanlar aynı olduğunda üsler toplanır:
2² × 2⁵ = 2²⁺⁵ = 2⁷.
2. 3³ × 3⁴ işleminin sonucu nedir?
a) 3⁷
b) 3²
c) 9⁷
d) 3⁶
Cevap: a) 3⁷
Çözüm: Aynı tabanlı üslü sayılarda çarpma işlemi yapılırken üsler toplanır:
3³ × 3⁴ = 3³⁺⁴ = 3⁷.
3. 2³ × 5² işleminin sonucu nedir?
a) 10⁵
b) 10
c) 8 × 25
d) 2⁵ × 5⁵
Cevap: c) 8 × 25
Çözüm: Tabanlar farklı olduğunda üslü sayılar çarpılırken tabanlar çarpılır ve sonuçlar hesaplanır:
2³ × 5² = 8 × 25 = 200.
Üslü Sayılarda Bölme İşlemi
1. 4⁶ ÷ 4² işleminin sonucu nedir?
a) 4⁸
b) 4⁴
c) 4²
d) 4³
Cevap: b) 4⁴
Çözüm: Üslü sayılarda bölme işlemi yapılırken tabanlar aynı olduğunda üsler çıkarılır:
4⁶ ÷ 4² = 4⁶⁻² = 4⁴.
2. 6⁵ ÷ 6³ işleminin sonucu nedir?
a) 6²
b) 6³
c) 6⁸
d) 6
Cevap: a) 6²
Çözüm: Aynı tabanlı üslü sayılarda bölme yapılırken üsler çıkarılır:
6⁵ ÷ 6³ = 6⁵⁻³ = 6².
3. 10⁸ ÷ 10² işleminin sonucu nedir?
a) 10¹⁰
b) 10⁶
c) 10⁴
d) 10
Cevap: b) 10⁶
Çözüm: Aynı tabanlı üslü sayılarda bölme işlemi yapılırken üsler çıkarılır:
10⁸ ÷ 10² = 10⁸⁻² = 10⁶.
Üslü Sayılarda İşlemler
1. (2³)² işleminin sonucu nedir?
a) 2⁵
b) 2⁶
c) 2¹²
d) 2⁹
Cevap: c) 2⁶
Çözüm: Üslü sayılarda üssün üssü alınırken üsler çarpılır:
(2³)² = 2³×² = 2⁶.
2. (3²)³ işleminin sonucu nedir?
a) 3⁶
b) 3⁵
c) 3⁷
d) 3⁸
Cevap: a) 3⁶
Çözüm: Üssün üssü alınırken üsler çarpılır:
(3²)³ = 3²×³ = 3⁶.
3. (5⁴ ÷ 5²)² işleminin sonucu nedir?
a) 5²
b) 5⁸
c) 5⁴
d) 5⁶
Cevap: c) 5⁴
Çözüm: Önce bölme işlemi yapılır:
5⁴ ÷ 5² = 5².
Sonra bu sonucun karesi alınır:
(5²)² = 5⁴.




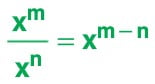
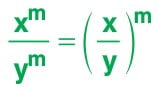












Teşekkürler
Bana cevap gönderi
Çok boş keşke bakmasaydim ilkokul değilde üst sınıf için söyleseydin
Şu 2. Sütünde 1-e 2.e var onları yanlışmı yazdınız veya yanlış yazdıysanız düzeltiniz
biriniz söyleyin artık tabanları farklı üsler eşit olan üslü ifadelerde nasıl toplama-çıkarma yapıcam yeter ya
gerçekten çok faydalı oldu çok iyi anladım teşekkür ederim
Teşekkürler…