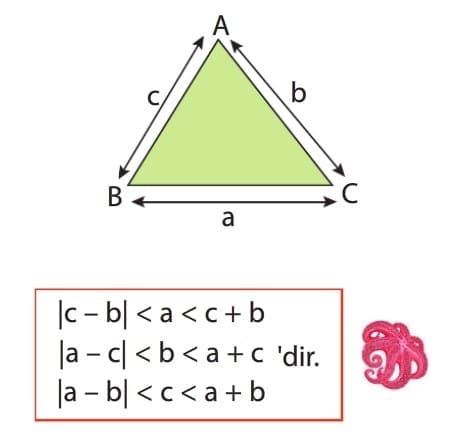
Bir üçgende kenarlardan birinin uzunluğu diğer iki kenarın uzunlukları toplamından küçük, uzunlukları farkının mutlak değerinden büyük olmalıdır.
Bu özelliği sağlamayan uzunluklar ile üçgen çizilemez.
Dikkat: Üç kenar uzunluğu ile bir üçgenin oluşturulup oluşturulamayacağı ile ilgili sorularda bir kenar uzunluğu üçgen eşitsizliğini sağlamıyorsa diğer kenar uzunlukları için sağlama yapmaya gerek yoktur.
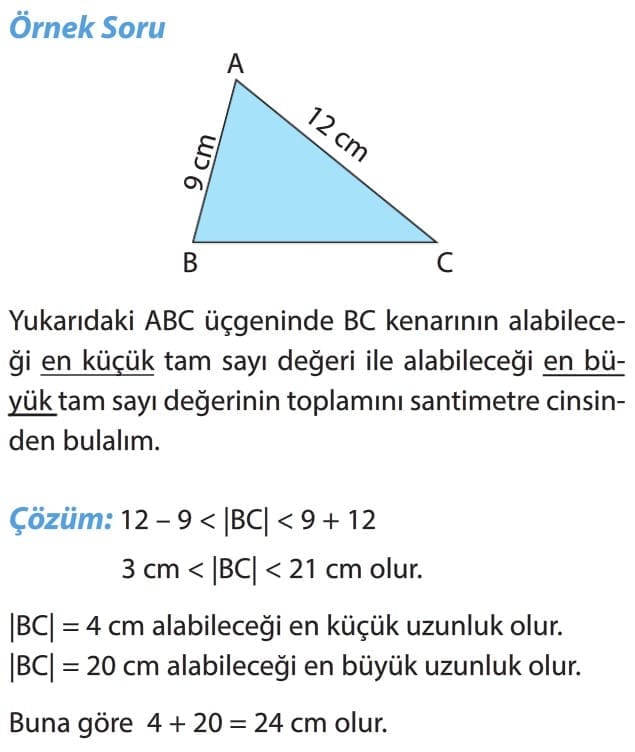
Örnek Soru: Yukarıdaki ABC üçgeninin iki kenar uzunluğu |AB| = 4 cm ve |AC| = 8 cm'dir. Buna göre, BC kenarının alabileceği tam sayı değerlerini bulalım.
Çözüm: BC kenar uzunluğu, diğer iki kenarın uzunlukları farkından büyük, uzunlukları toplamından küçük olacağından
8 - 4 < |BC| < 8 + 4
4 cm < |BC| < 12 cm olur.
BC kenar uzunluğu, 4 cm'den büyük ve 12 cm'den küçük tam sayı değerlerini alabilir.
|BC| = 5 cm, |BC| = 6 cm, |BC| = 7 cm ..... .. |BC| = 11 cm
Sonuç olarak 5 cm, 6 cm, 7 cm, 8 cm, 9 cm, 10 cm ve 11 cm olmak üzere 7 tane farklı tam sayı değeri olabilir.
Örnek Soru: Yukarıda uzunlukları verilen çubuklar uç uca eklenerek üçgen oluşturulabilir mi?
Çözüm: Verilen üç çubuk uzunluğunun her birinin üçgen eşitsizliğini sağlayıp sağlamadığına bakalım.
|AB| = 6 cm,|CD| + |EF| = 12 + 5 = 17 cm ve |CD| - |EF| = 12 - 5 = 7 cm olur.
Buna göre |AB| = 6 cm'lik uzunluk diğer iki kenarın uzunlukları toplamı 17 cm'den küçük ama diğer kenar uzunlukları farkı olan 7 cm'den büyük olmadığı için bu çubuklarla üçgen oluşturulamaz.
Örnek Soru: Yukarıda uzunlukları verilen çubuklar uç uca eklenerek üçgen oluşturulabilir mi?
Çözüm: Verilen üç çubuk uzunluğu için tek tek üçgen eşitsizliğini sağlayıp sağlamadığına bakalım.
|AB| = 6 cm,|CD| + |EF| = 8 + 4 = 12 cm ve |CD| - |EF| = 8 - 4 = 4 cm'dir. Buna göre, 4 < 6 < 12 olur.
|CD| = 8, |AB| + |EF| = 6 + 4 = 10 cm ve |AB| - |EF| = 6 - 4 = 2 cm'dir. Buna göre, 2 < 8 < 10 olur.
|EF| =4, |CD| + |AB| =8+6= 14 cm ve |CD| - |AB| = 8 - 6 = 2 cm'dir. Buna göre, 2 < 4 < 14 olur.
Görüldüğü gibi üç kenar uzunluğundan her birinin kenar uzunluğu diğer iki kenarın uzunlukları toplamından küçük ve farkından büyüktür. Bu nedenle de bu çubuklarla üçgen oluşturulabilir.
Örnek Soru: Yukarıdaki sokak lambaları arasındaki uzaklıklar metre cinsinden verilmiştir. Buna göre, aralarındaki uzaklığı verilmeyen iki sokak lambası arasındaki mesafenin metre cinsinden hangi tam sayı değerlerini alabileceğini bulalım.
Çözüm: Sokak lambalarını üçgenlerin köşeleri gibi düşünebiliriz. Şekilde iki tane üçgen vardır ve [AC] iki üçgeninde ortak kenarıdır. Bu nedenle x değeri her iki üçgeni de sağlamalıdır. ABC üçgeninde 90 - 60 < x < 90 + 60 ise 30 < x < 150
ACD üçgeninde 150 - 50 < x < 150 + 50 ise 100 < x < 200
Buna göre, her iki şartı sağlayan x değerlerini ortak çözüm yaparak buluruz. Her iki eşitsizliği de sağlayan x değerleri 100 m < x <150 m aralığındaki tüm tam sayı değerlerini alabilir.