Üçgenlerin eşlik koşulları, iki üçgenin tüm açı ve kenarlarının birebir aynı olduğu durumları tanımlar. Eş üçgenler, aynı şekle ve büyüklüğe sahiptir, ancak farklı konumlarda olabilirler. Üçgenlerin eş olduğunu belirlemek için SSS (Sıra-Sıra-Sıra), SAS (Sıra-Açı-Sıra) ve ASA (Açı-Kenar-Açı) kriterleri kullanılır. Bu kriterler, üçgenlerin tüm özelliklerini karşılaştırarak eşlik durumunu belirler. Eşlik kuralları, geometri problemlerinde simetriyi anlamayı kolaylaştırır ve gerçek hayatta mimari tasarımlar ile mühendislik projelerinde büyük bir öneme sahiptir. Yeni müfredat, bu kavramları günlük hayattan alınan hikayelerle ilişkilendirerek öğrencilerin analitik düşünme ve problem çözme becerilerini geliştirmeyi amaçlar.

Üçgenlerin Eş veya Benzer Olma Koşulları Testleri

---

Üçgenlerde Eşlik (Üçgenlerin Eş Olma Koşulları) Ders Notu (Yeni Müfredat)

Çözümlü Sorular

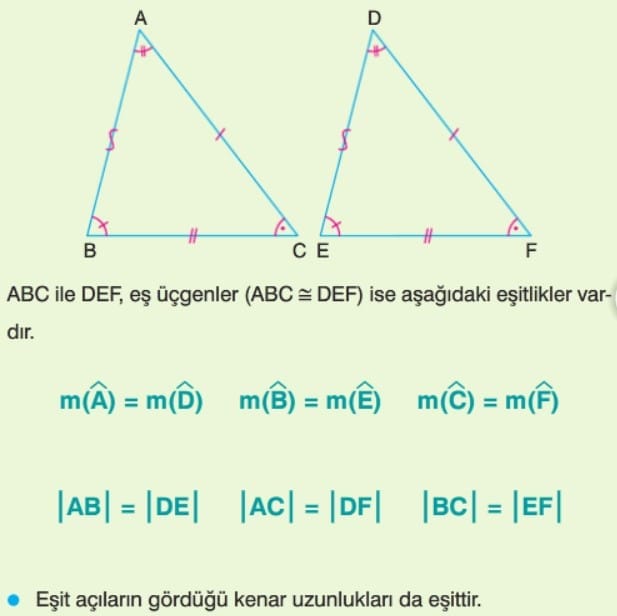
Eşlik Aksiyomları

1. Kenar – Açı – Kenar (K.A.K.) Eşliği

 

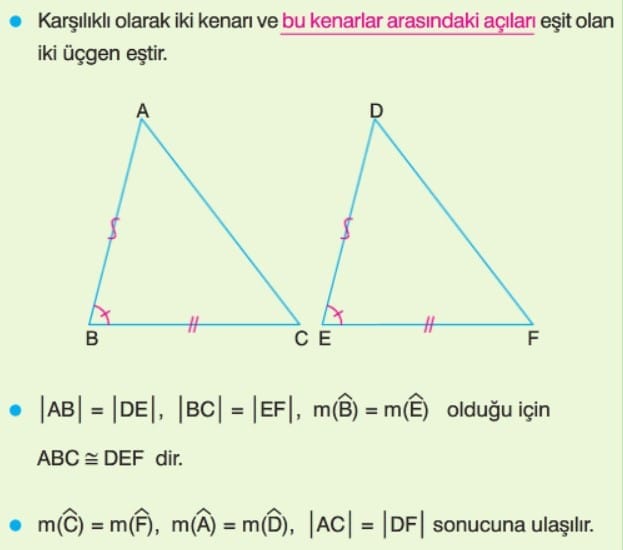
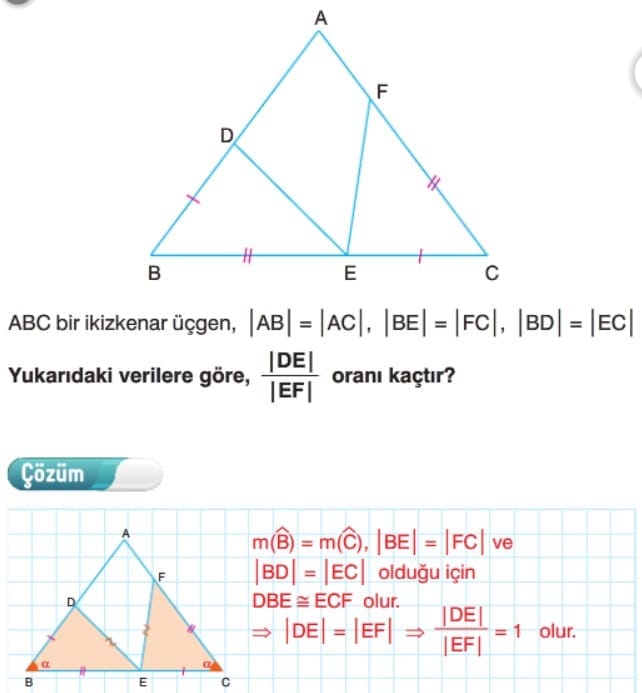
2. Açı – Kenar – Açı (A.K.A.) Eşliği

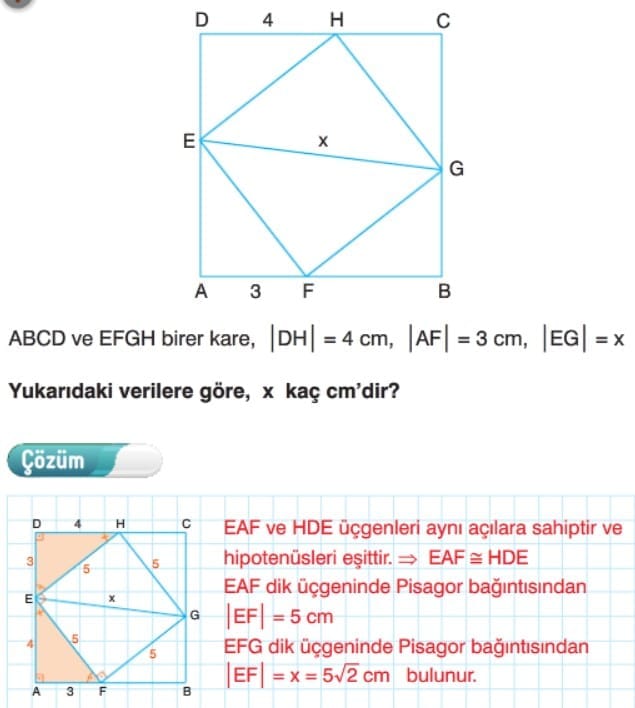
3. Kenar – Kenar – Kenar (A.K.A.) Eşliği

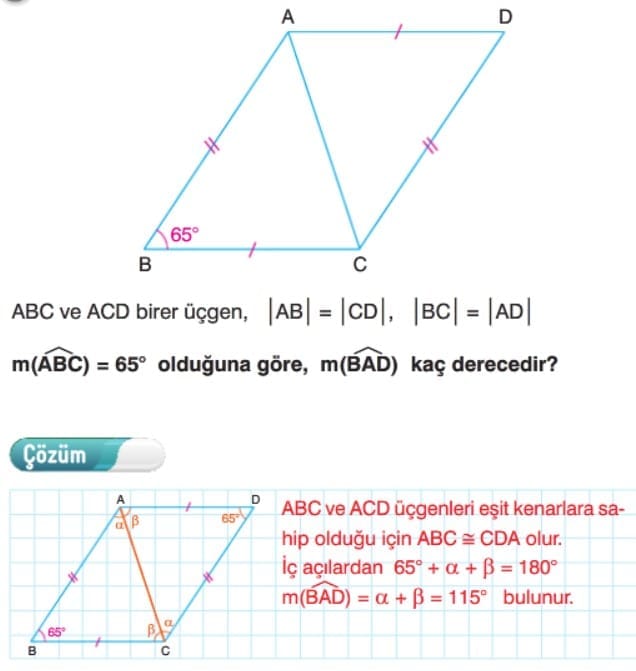
Eş Üçgenlerin Yardımcı Elemanları

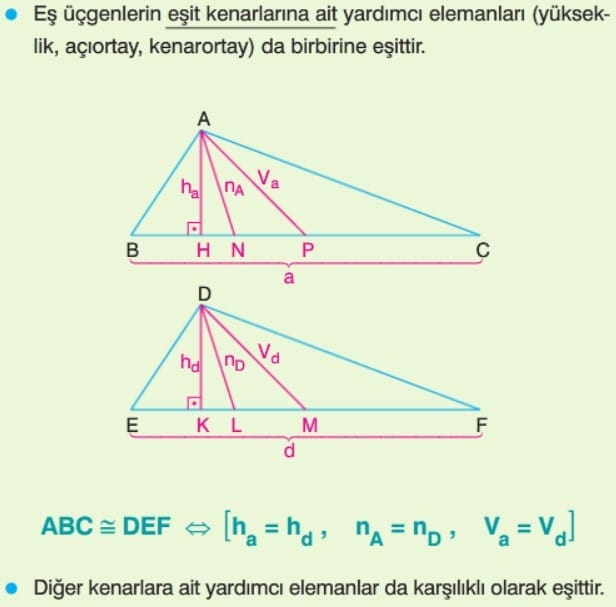
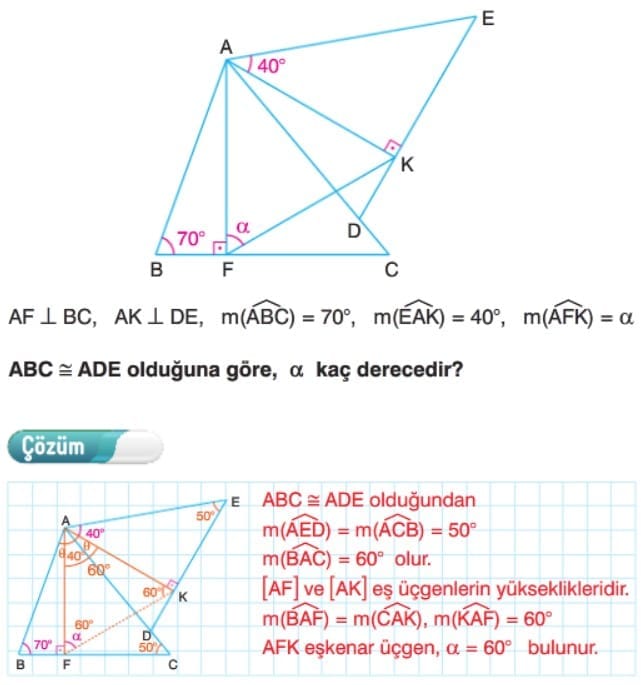
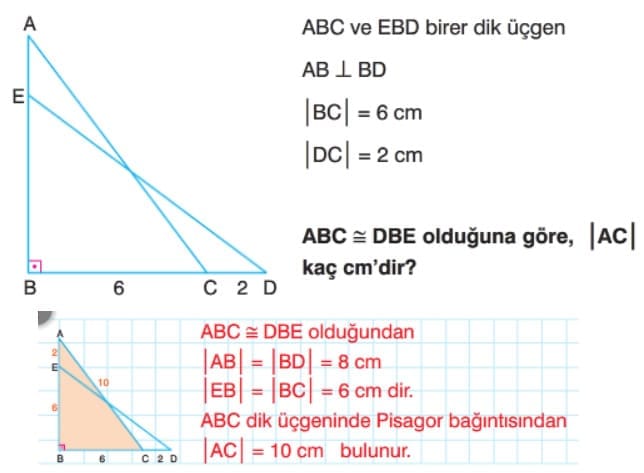
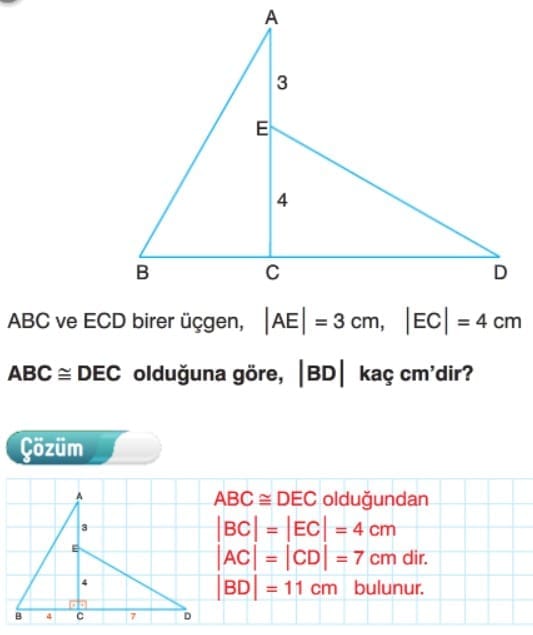
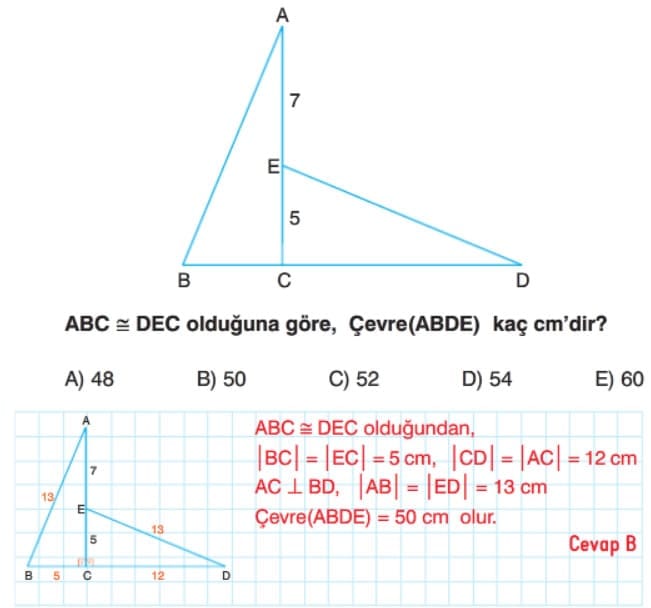
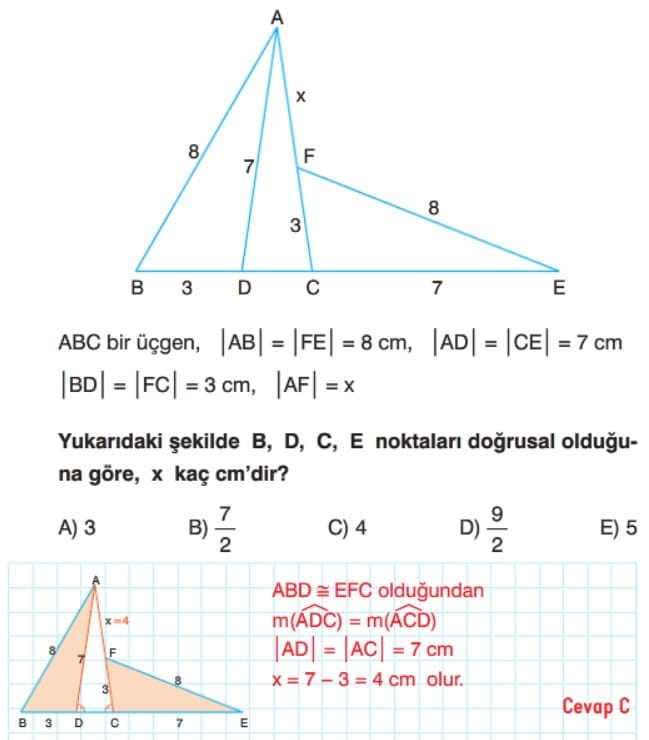
Üçgenlerde Eşlik Çözümlü Sorular

---

Çözümlü Örnek Test Soruları

1. Soru
Bir üçgenin kenar uzunlukları 6 cm, 8 cm ve 10 cm’dir. Bu üçgen ile eş olan başka bir üçgenin kenar uzunlukları aşağıdakilerden hangisidir?
a) 3 cm, 4 cm, 5 cm
b) 6 cm, 8 cm, 10 cm
c) 9 cm, 12 cm, 15 cm
d) 12 cm, 16 cm, 20 cm
e) 15 cm, 20 cm, 25 cm

Çözüm:
Eş üçgenlerde tüm kenar uzunlukları birebir aynıdır. Bu nedenle eş üçgenin kenar uzunlukları 6 cm, 8 cm ve 10 cm olacaktır.
Cevap: b) 6 cm, 8 cm, 10 cm

---

2. Soru
Bir üçgenin açıları 50°, 60° ve 70°’dir. Bu üçgenle eş olan başka bir üçgenin açı ölçüleri nedir?
a) 40°, 60°, 80°
b) 50°, 60°, 70°
c) 50°, 70°, 80°
d) 60°, 60°, 60°
e) 45°, 60°, 75°

Çözüm:
Eş üçgenlerde tüm açılar birebir aynı olmalıdır. Bu nedenle açı ölçüleri 50°, 60° ve 70° olacaktır.
Cevap: b) 50°, 60°, 70°

---

3. Soru
İki üçgenin eş olduğunu belirlemek için aşağıdaki kriterlerden hangisi kullanılabilir?
a) AA
b) SSS
c) Benzerlik
d) Açı-Kenar-Bağımsız
e) Orantı

Çözüm:
İki üçgenin eş olduğunu belirlemek için SSS (Sıra-Sıra-Sıra), SAS (Sıra-Açı-Sıra) ve ASA (Açı-Kenar-Açı) kriterleri kullanılır.
Cevap: b) SSS

---

4. Soru
Bir üçgende iki kenar sırasıyla 5 cm ve 7 cm, aralarındaki açı ise 60°’dir. Bu üçgenle eş olan başka bir üçgenin aralarındaki açı ölçüsü nedir?
a) 60°
b) 50°
c) 70°
d) 80°
e) 90°

Çözüm:
Eş üçgenlerde eşlik kriterlerine göre açılar birebir aynı olmalıdır. Bu nedenle aralarındaki açı da 60° olacaktır.
Cevap: a) 60°

---

5. Soru
Bir üçgenin kenar uzunlukları 9 cm, 12 cm ve 15 cm’dir. Bu üçgen ile eş olan başka bir üçgenin kenar uzunlukları aşağıdakilerden hangisi olamaz?
a) 9 cm, 12 cm, 15 cm
b) 12 cm, 15 cm, 9 cm
c) 15 cm, 9 cm, 12 cm
d) 10 cm, 15 cm, 20 cm
e) 9 cm, 15 cm, 12 cm

Çözüm:
Eş üçgenlerde tüm kenarlar birebir aynı olmalıdır. 10 cm, 15 cm, 20 cm olan kenarlar eşlik koşulunu sağlamaz.
Cevap: d) 10 cm, 15 cm, 20 cm

---

6. Soru
Bir üçgenin açıları sırasıyla 45°, 45° ve 90°’dir. Bu üçgenle eş olan bir üçgenin hipotenüsü 14 cm ise, kısa kenarların uzunlukları nedir?
a) 7 cm ve 7 cm
b) 8 cm ve 8 cm
c) 9 cm ve 9 cm
d) 10 cm ve 10 cm
e) 12 cm ve 12 cm

Çözüm:
45°-45°-90° üçgeninde hipotenüs = $x\surd 2$, kısa kenarlar = x.
$14=x\surd 2$, $x=14/\surd 2=7\surd 2$.
Cevap: a) 7 cm ve 7 cm

---

7. Soru
İki üçgenin eş olduğunu anlamak için aşağıdaki kriterlerden hangisi yeterlidir?
a) İki açı ve bir kenarın eşit olması
b) Sadece iki kenarın eşit olması
c) Tüm kenarların orantılı olması
d) İki açının eşit olması
e) Sadece bir kenarın eşit olması

Çözüm:
Eşlik için ASA (Açı-Kenar-Açı) kriteri yeterlidir.
Cevap: a) İki açı ve bir kenarın eşit olması

---

8. Soru
Bir üçgenin kenar uzunlukları 5 cm, 12 cm ve 13 cm’dir. Eş olan başka bir üçgenin en uzun kenarı nedir?
a) 5 cm
b) 12 cm
c) 13 cm
d) 15 cm
e) 20 cm

Çözüm:
Eş üçgenlerde kenarlar birebir aynı olmalıdır. En uzun kenar 13 cm’dir.
Cevap: c) 13 cm

---

9. Soru
Bir üçgende iki kenar sırasıyla 8 cm ve 10 cm, aralarındaki açı ise 90°’dir. Bu üçgenle eş olan başka bir üçgenin kısa kenar uzunluğu nedir?
a) 8 cm
b) 6 cm
c) 10 cm
d) 12 cm
e) 15 cm

Çözüm:
Eş üçgenlerde kenar uzunlukları birebir aynı olmalıdır. Kısa kenar 8 cm’dir.
Cevap: a) 8 cm

---

10. Soru
Bir üçgenin kenar uzunlukları 7 cm, 24 cm ve 25 cm’dir. Bu üçgenin hipotenüsü nedir?
a) 24 cm
b) 25 cm
c) 7 cm
d) 20 cm
e) 30 cm

Çözüm:
7, 24, 25 bir dik üçgenin kenarlarıdır. Hipotenüs 25 cm’dir.
Cevap: b) 25 cm