Üçgenlerde Benzerlik (Üçgenlerin Benzer Olma Koşulları) 9. Sınıf Matematik (Yeni Müfredat)
Üçgenlerin benzerlik koşulları, iki üçgenin açıların eşit ve kenarların orantılı olduğu durumları ifade eder. Benzer üçgenler, aynı şekle sahip olmakla birlikte, ölçekleri farklı olabilir. Üçgenlerin benzer olduğunu anlamak için AA (Açı-Açı), KAK (Kenar-Açı-Kenar) ve KKK (Kenar-Kenar-Kenar) kriterleri kullanılır. Bu kurallar, günlük hayatta haritaların ölçeklenmesinden mimari tasarımlara kadar birçok alanda kullanılmaktadır. Benzerlik kuralları sayesinde, oran ve orantı ile karmaşık problemler basit hale getirilebilir. Yeni müfredat, benzerlik konusunu gerçek hayattan örneklerle pekiştirerek öğrencilerin problem çözme becerilerini geliştirmeyi amaçlamaktadır.
9. Sınıf Üçgenlerin Eş veya Benzer Olma Koşulları Testleri
9. Sınıf Üçgenlerin Benzer Olma Koşulları Ders Notu (Yeni Müfredat)
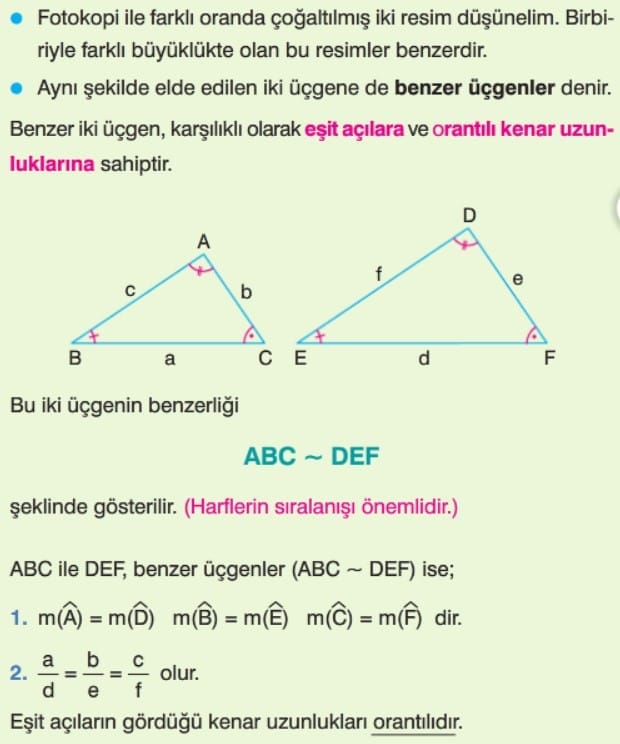
Benzerlik Kavramı
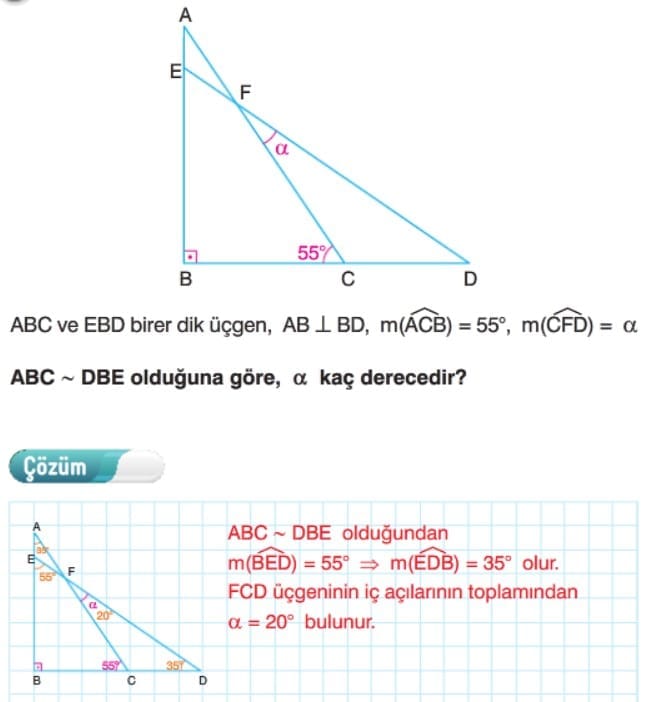
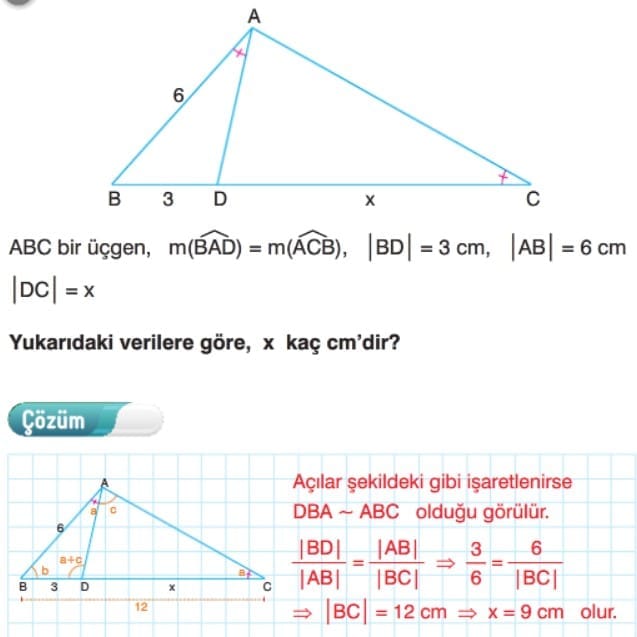
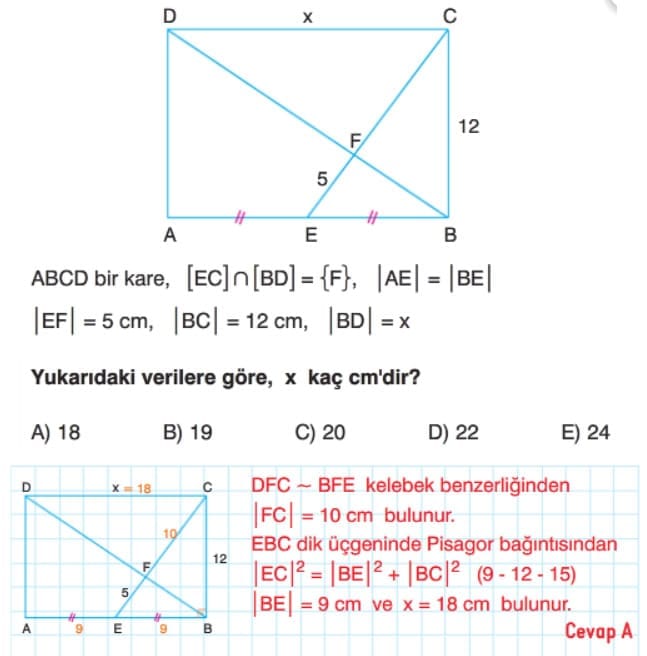
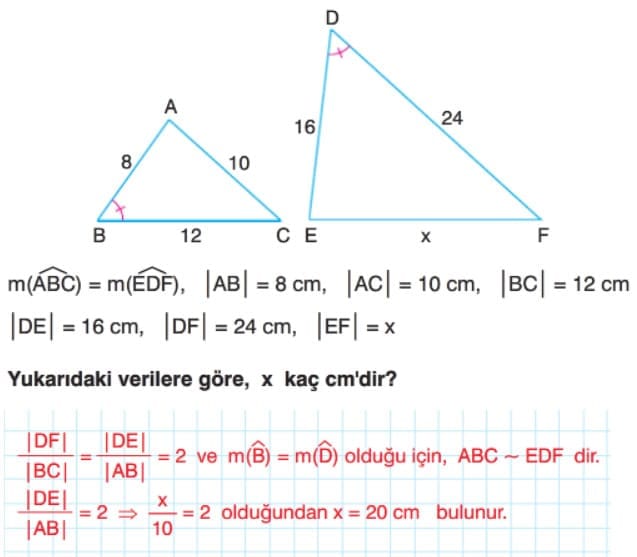
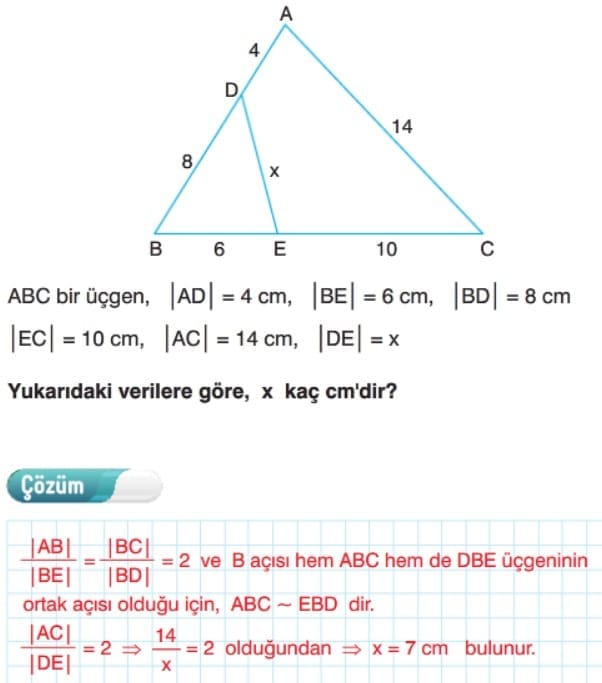
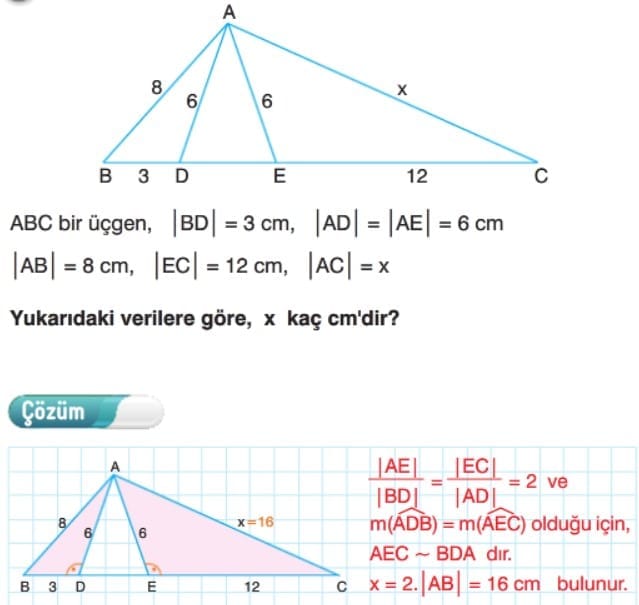
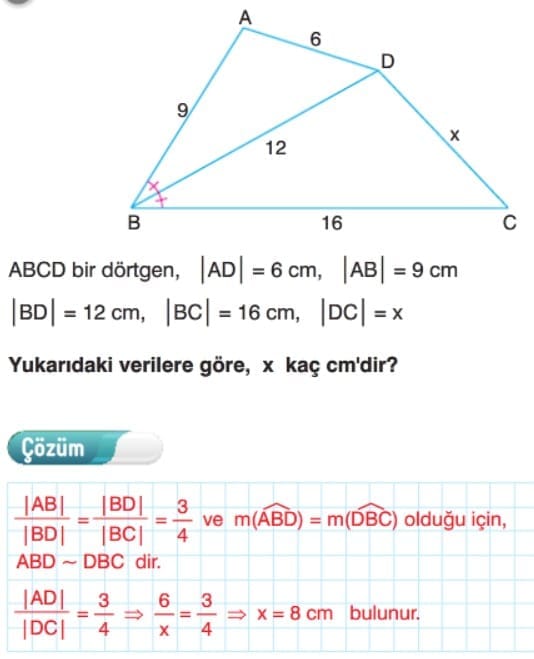
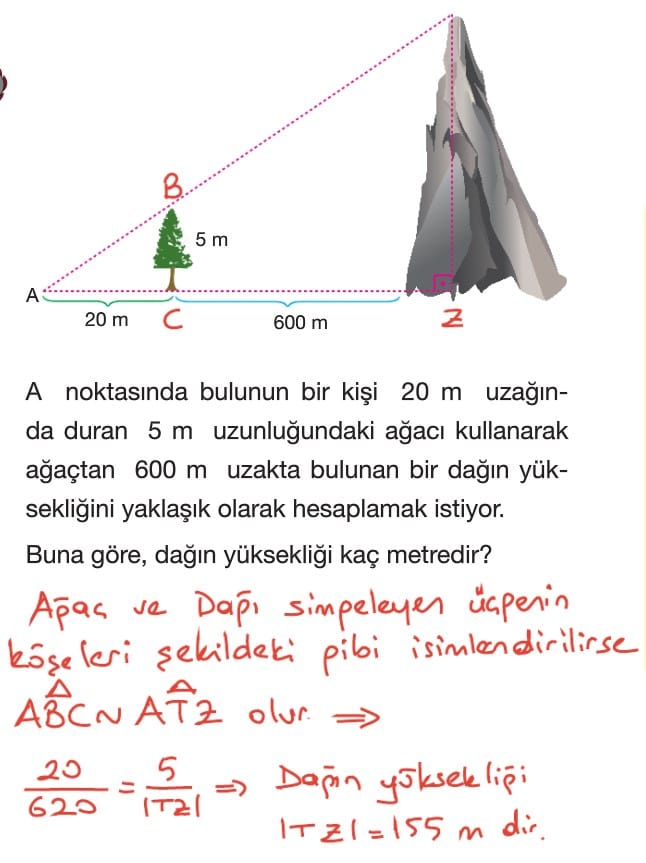
Çözümlü Sorular
Benzerlik Aksiyomları
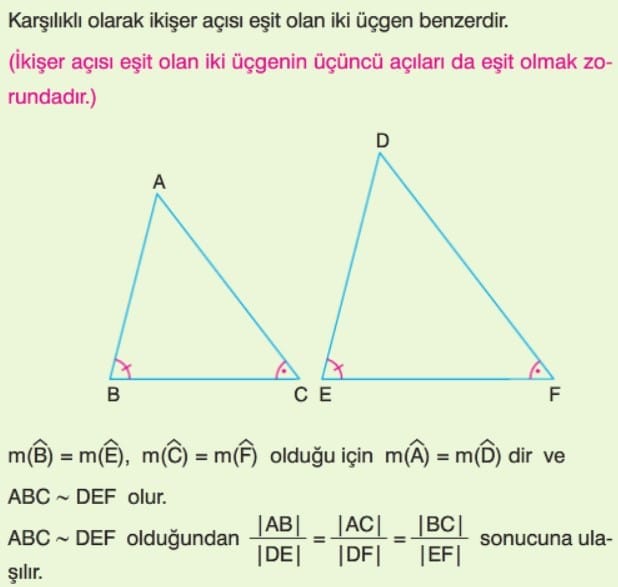
Açı Açı Benzerlik Teoremi (A.A)
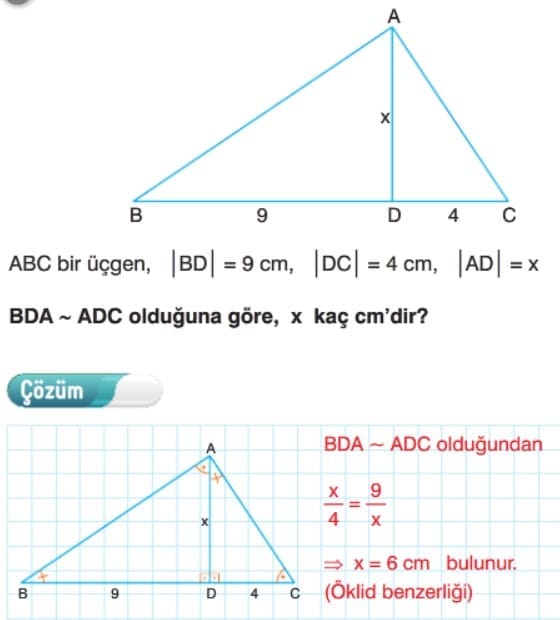
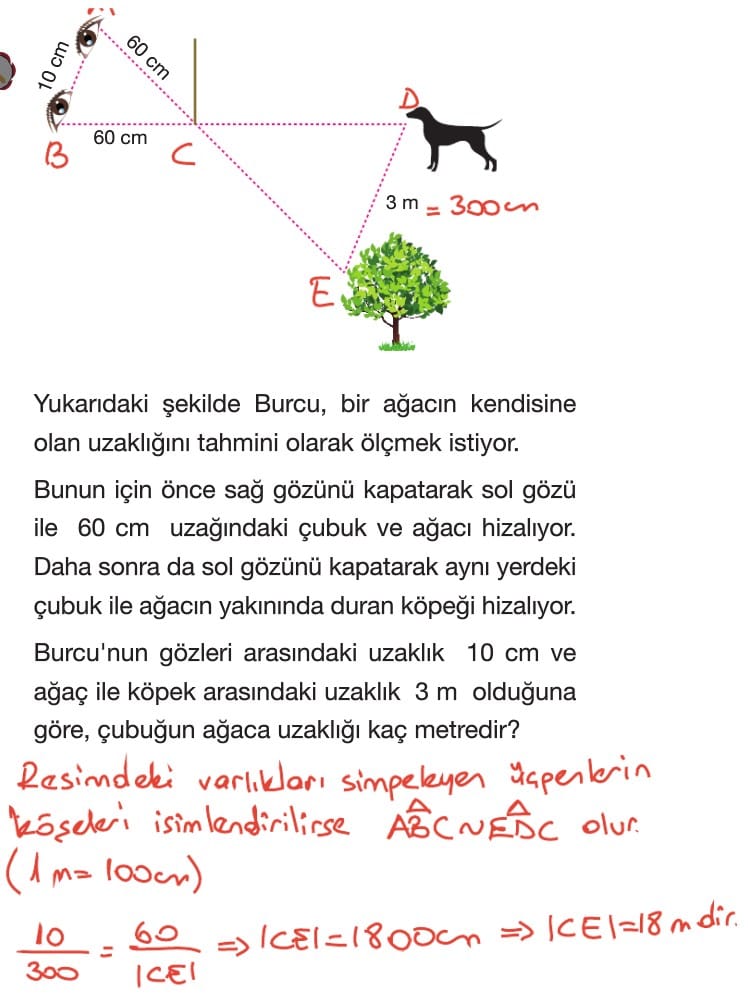
Çözümlü Sorular
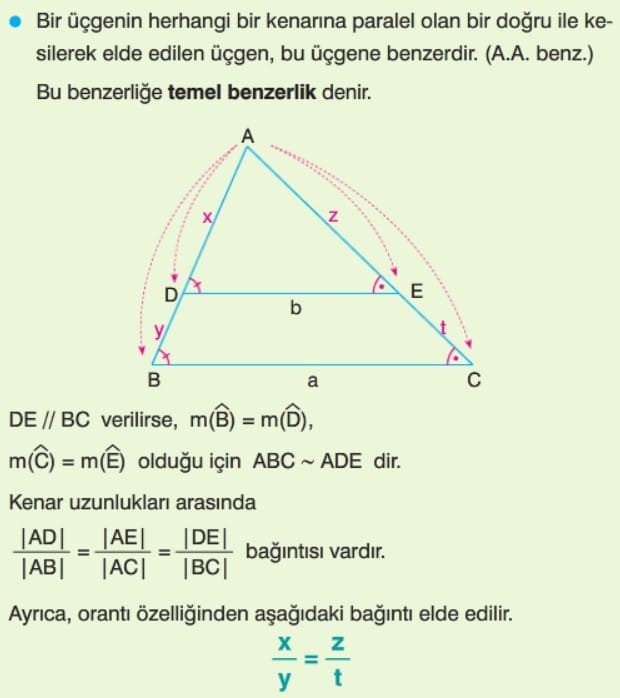
Temel Benzerlik Teoremi (Temel Orantı Teoremi)
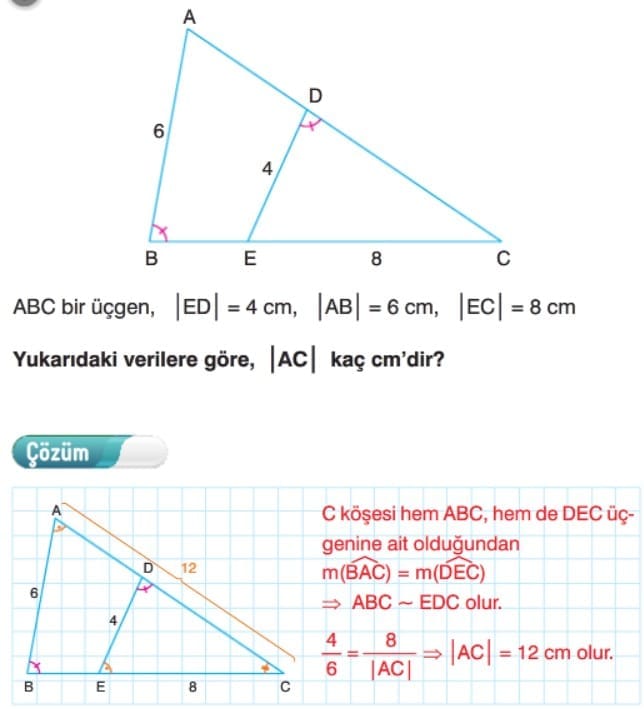
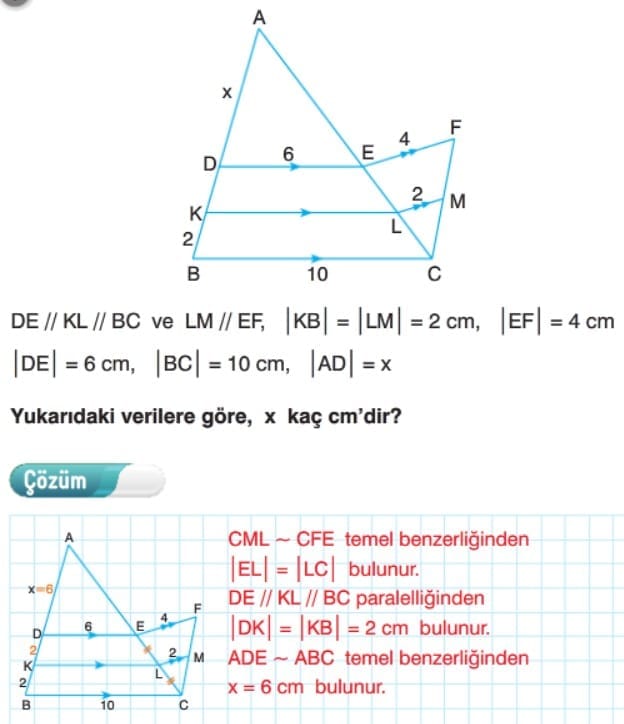
Çözümlü Sorular
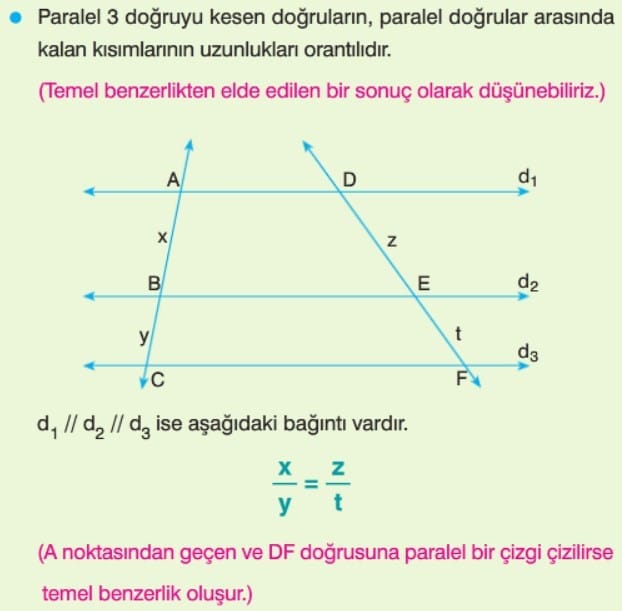
Tales Teoremi
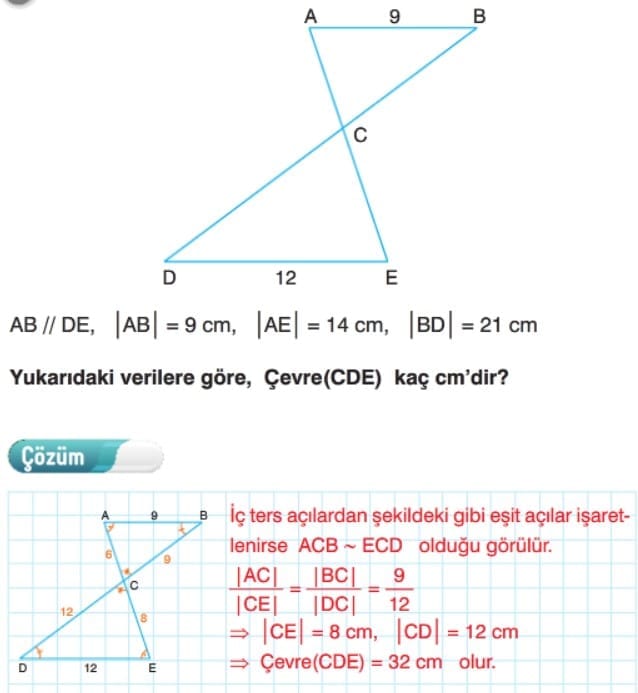
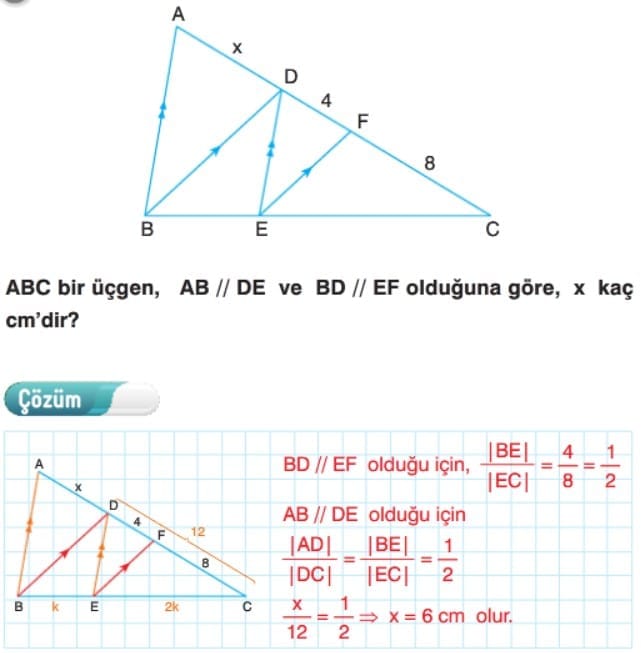
Çözümlü Sorular
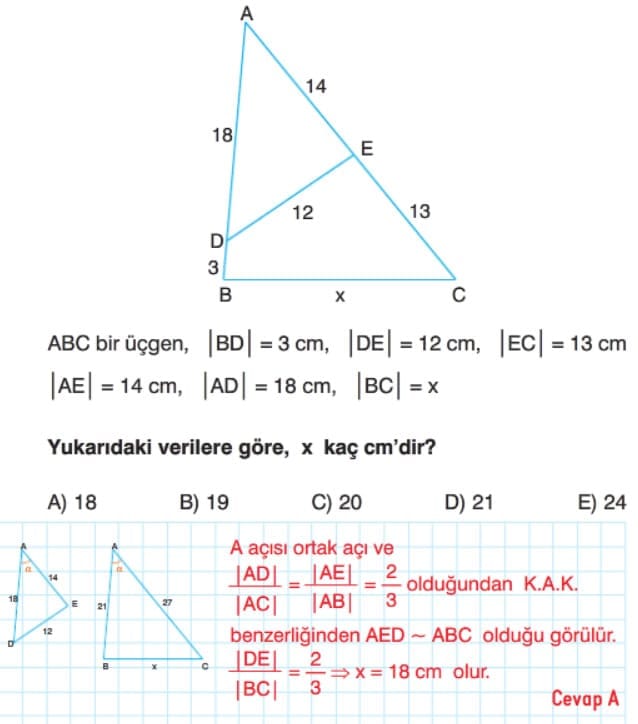
Kenar Açı Kenar Benzerlik Teoremi

Çözümlü Sorular
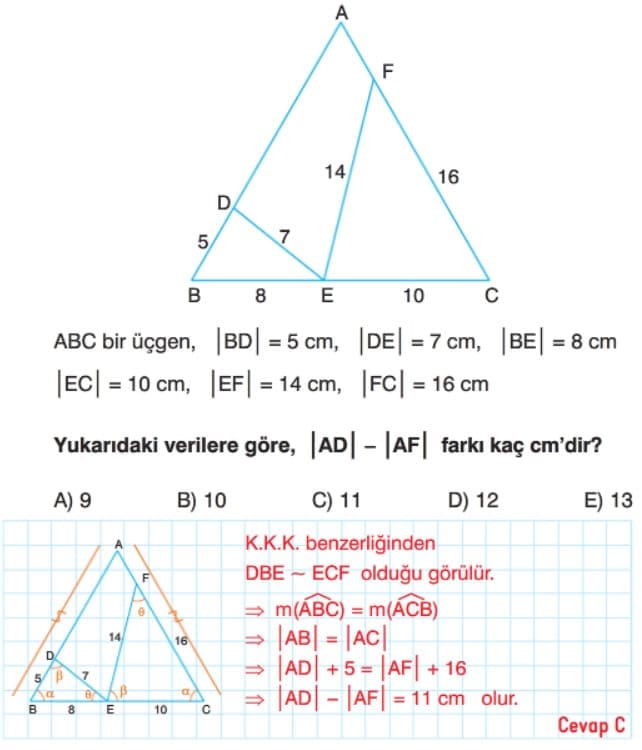
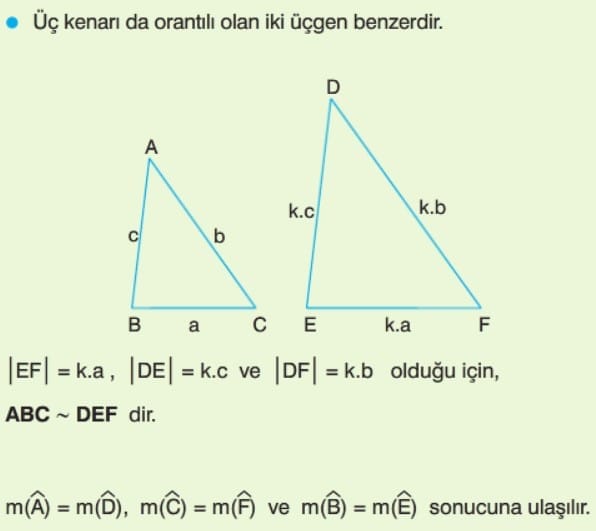
Kenar Kenar Kenar Benzerlik Teoremi
Çözümlü Sorular
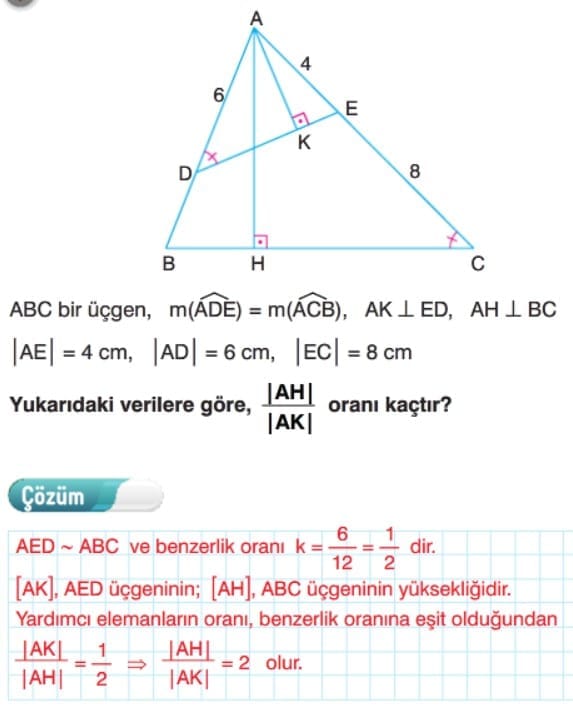
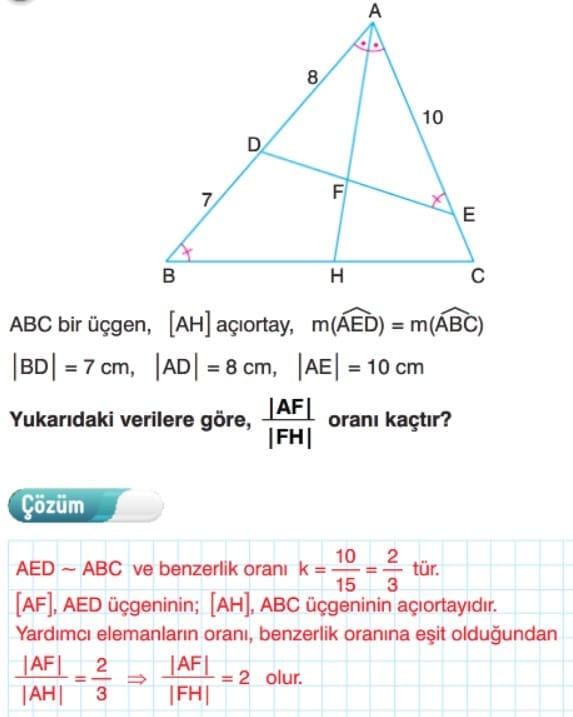
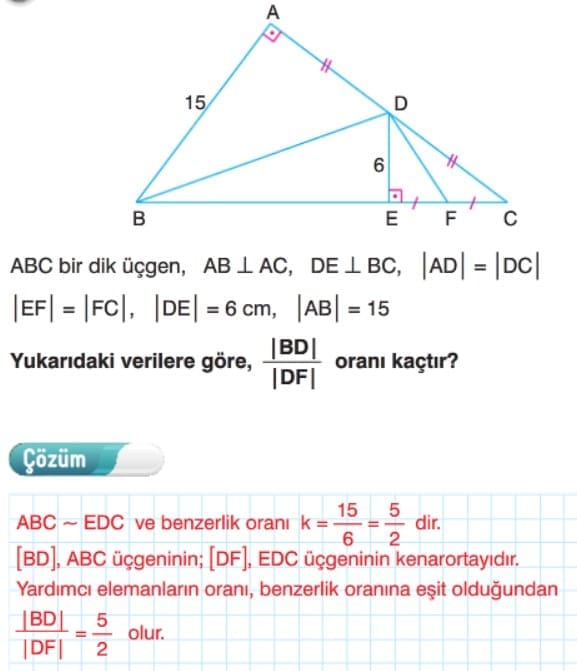
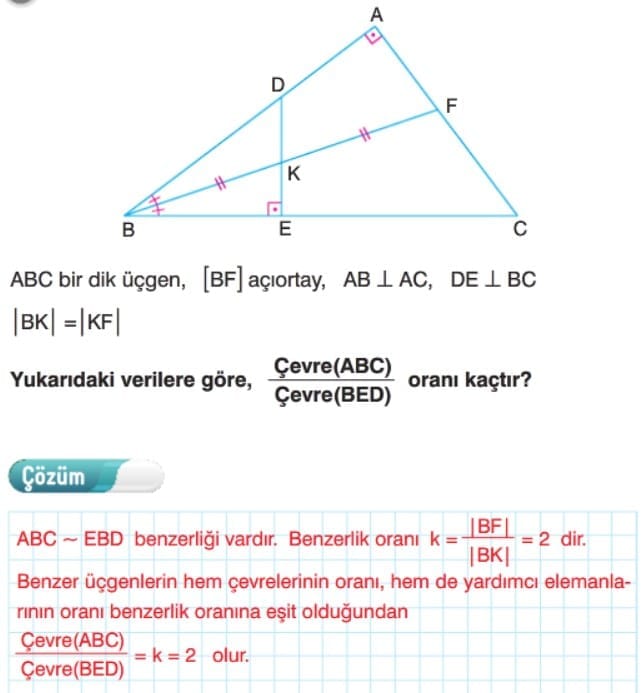
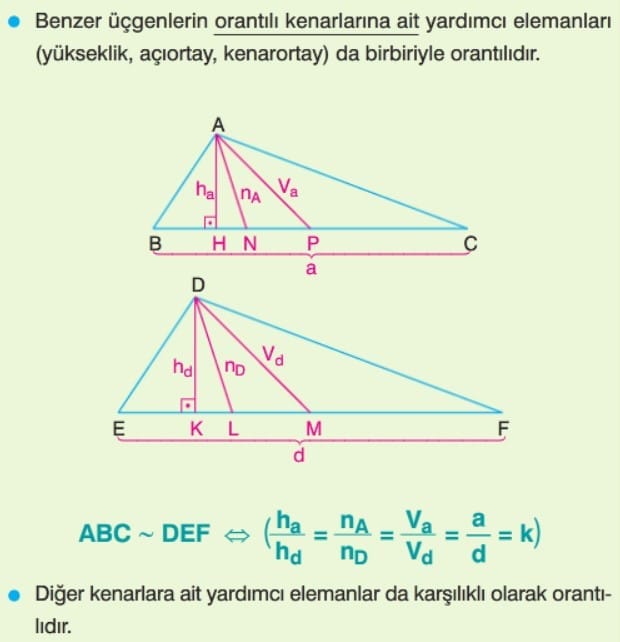
Benzer Üçgenlerde Yardımcı Elemanlar
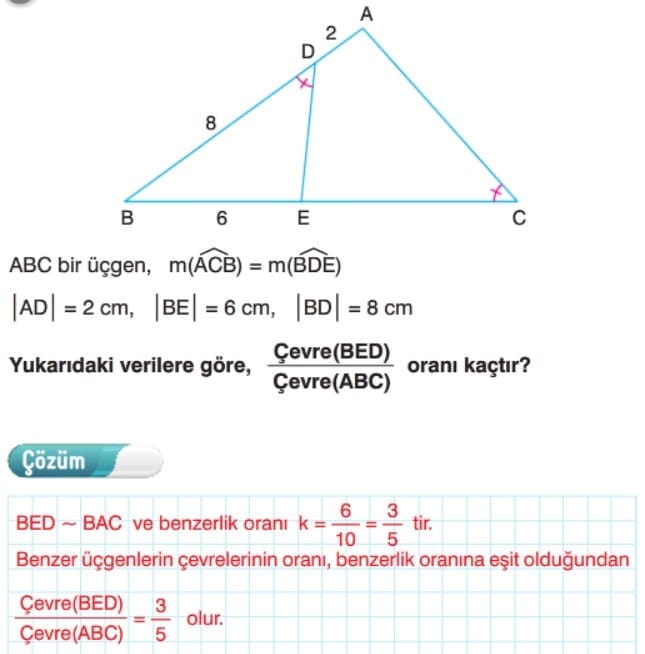
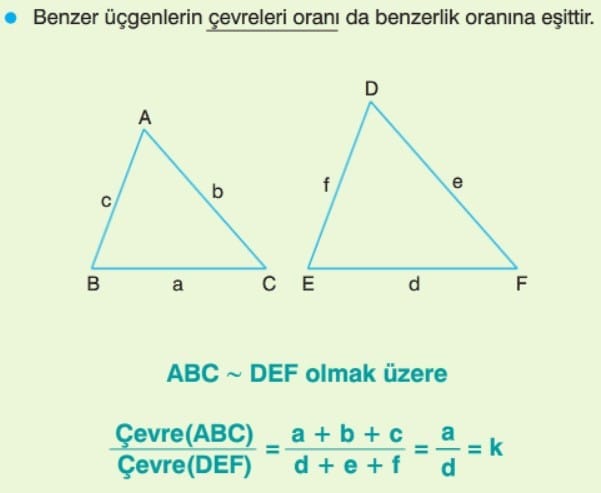
Benzer Üçgenlerin Çevreleri
Çözümlü Sorular
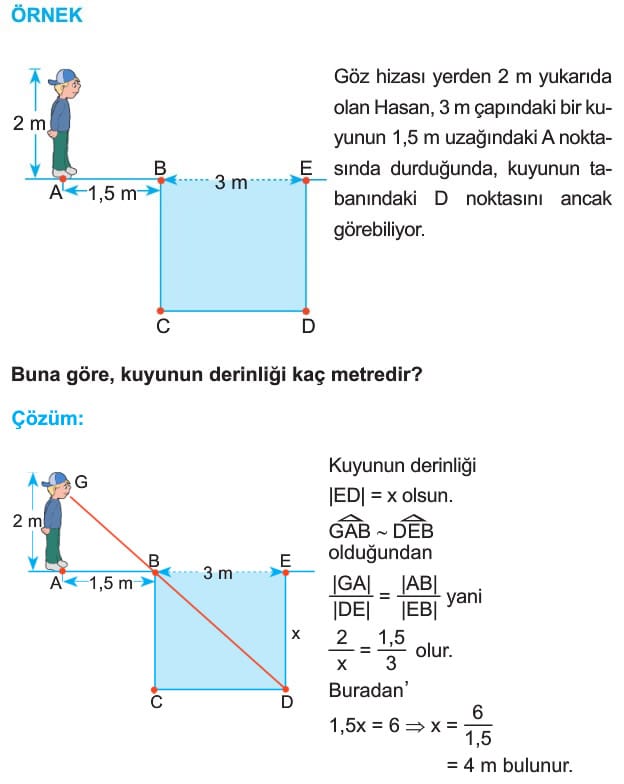
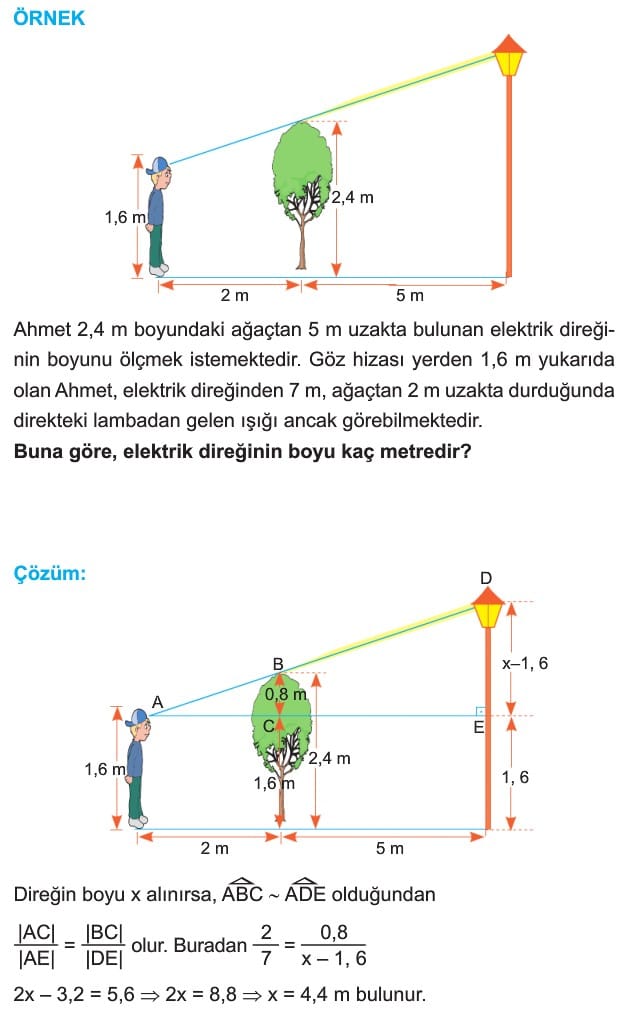
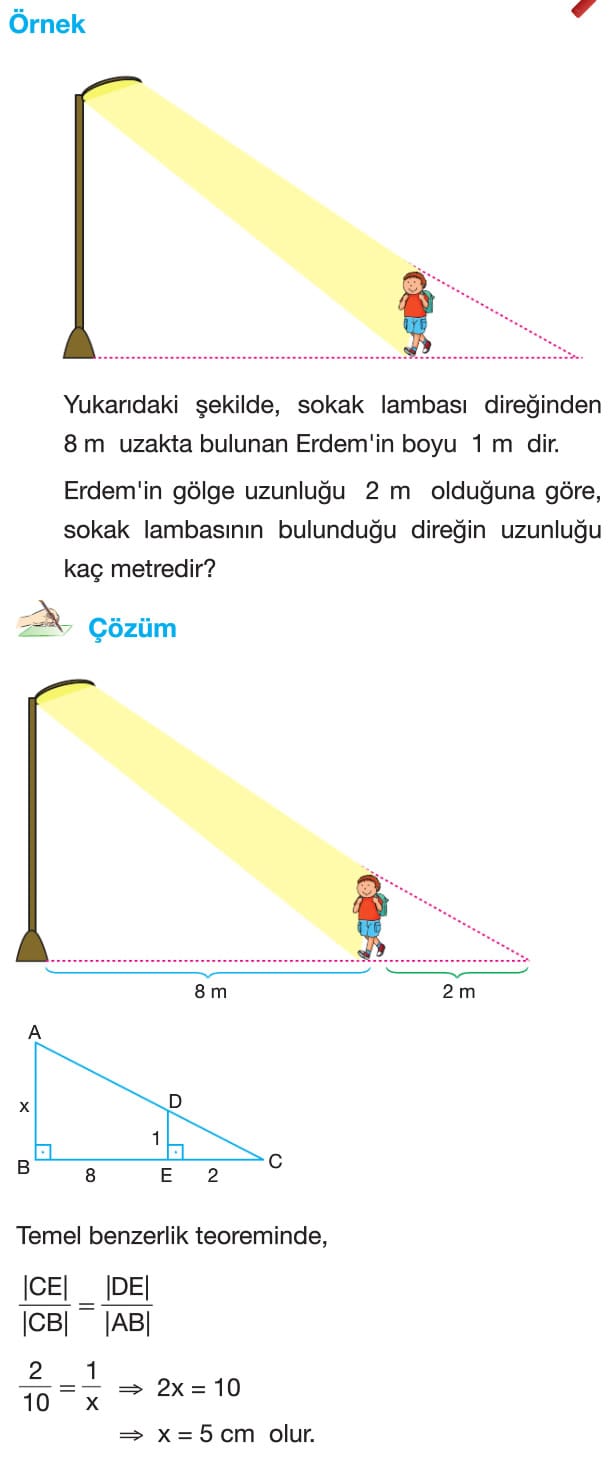
Benzerlikle İlgili Uygulamalar
Çözümlü Örnek Test Soruları
1. Soru
Bir üçgenin kenar uzunlukları 5 cm, 12 cm ve 13 cm’dir. Benzer olan bir üçgende en uzun kenar 26 cm ise, diğer kenarlar kaç cm’dir?
a) 10 ve 24
b) 8 ve 20
c) 15 ve 30
d) 9 ve 18
e) 11 ve 22
Çözüm:
Oran: 26 ÷ 13 = 2
Diğer kenarlar:
5 × 2 = 10, 12 × 2 = 24
Cevap: a) 10 ve 24
2. Soru
Bir üçgenin açıları 30°, 60° ve 90°’dir. Benzer olan bir üçgende 30°’nin karşısındaki kenar 6 cm ise, hipotenüs kaç cm’dir?
a) 10
b) 12
c) 18
d) 24
e) 30
Çözüm:
30°-60°-90° üçgeninde, hipotenüs = 2 × kısa kenar.
Hipotenüs = 2 × 6 = 12
Cevap: b) 12
3. Soru
Bir üçgenin kenar uzunlukları 3 cm, 4 cm ve 5 cm’dir. Benzer olan bir üçgende en küçük kenar 9 cm ise, diğer kenarlar kaç cm’dir?
a) 12 ve 15
b) 10 ve 13
c) 14 ve 18
d) 11 ve 16
e) 10 ve 14
Çözüm:
Oran: 9 ÷ 3 = 3
Diğer kenarlar:
4 × 3 = 12, 5 × 3 = 15
Cevap: a) 12 ve 15
4. Soru
Bir üçgenin açıları 45°, 45° ve 90°’dir. Benzer bir üçgende hipotenüs 14 cm ise, kısa kenarlar kaç cm’dir?
a) 5 ve 5
b) 7 ve 7
c) 8 ve 8
d) 6 ve 6
e) 9 ve 9
Çözüm:
45°-45°-90° üçgeninde, hipotenüs = √2 × kısa kenar.
Kısa kenar = 14 ÷ √2 = 14 × (√2 ÷ 2) = 7√2
Cevap: b) 7 ve 7
5. Soru
Bir üçgenin kenar uzunlukları 7 cm, 24 cm ve 25 cm’dir. Benzer bir üçgende en uzun kenar 50 cm olduğuna göre, diğer kenarlar kaç cm’dir?
a) 14 ve 48
b) 21 ve 42
c) 28 ve 49
d) 35 ve 70
e) 18 ve 30
Çözüm:
Oran: 50 ÷ 25 = 2
Diğer kenarlar:
7 × 2 = 14, 24 × 2 = 48
Cevap: a) 14 ve 48
6. Soru
Bir üçgenin kenar uzunlukları 6 cm, 8 cm ve 10 cm’dir. Benzer bir üçgende en uzun kenar 20 cm ise, diğer kenarlar kaç cm’dir?
a) 12 ve 16
b) 10 ve 15
c) 11 ve 14
d) 13 ve 17
e) 8 ve 12
Çözüm:
Oran: 20 ÷ 10 = 2
Diğer kenarlar:
6 × 2 = 12, 8 × 2 = 16
Cevap: a) 12 ve 16
7. Soru
Bir üçgenin açıları 40°, 60° ve 80°’dir. Benzer bir üçgende 40°’nin karşısındaki kenar 15 cm, 80°’nin karşısındaki kenar 21 cm ise, 60°’nin karşısındaki kenar kaç cm’dir?
a) 18
b) 24
c) 20
d) 22
e) 25
Çözüm:
Oran: 15 ÷ 21 = 5 ÷ 7
60°’nin karşısındaki kenar:
(5 ÷ 7) × 24 = 18
Cevap: a) 18
8. Soru
Bir üçgenin kenar uzunlukları 5 cm, 12 cm ve 13 cm’dir. Benzer bir üçgende en uzun kenar 39 cm olduğuna göre, diğer kenarlar kaç cm’dir?
a) 15 ve 36
b) 10 ve 28
c) 16 ve 40
d) 18 ve 42
e) 20 ve 48
Çözüm:
Oran: 39 ÷ 13 = 3
Diğer kenarlar:
5 × 3 = 15, 12 × 3 = 36
Cevap: a) 15 ve 36
9. Soru
Bir dik üçgende kısa kenar 5 cm, uzun kenar 12 cm ve hipotenüs 13 cm’dir. Benzer bir üçgende kısa kenar 10 cm olduğuna göre, uzun kenar kaç cm’dir?
a) 24
b) 20
c) 18
d) 15
e) 25
Çözüm:
Oran: 10 ÷ 5 = 2
Uzun kenar:
12 × 2 = 24
Cevap: a) 24
10. Soru
Bir üçgenin kenar uzunlukları 3 cm, 4 cm ve 5 cm’dir. Benzer bir üçgende en uzun kenar 10 cm ise, diğer kenarlar kaç cm’dir?
a) 6 ve 8
b) 9 ve 12
c) 5 ve 7
d) 8 ve 10
e) 4 ve 6
Çözüm:
Oran: 10 ÷ 5 = 2
Diğer kenarlar:
3 × 2 = 6, 4 × 2 = 8
Cevap: a) 6 ve 8