Üçgenlerde eşlik ve benzerlik, geometrinin temel konularından biridir. Eşlik, iki üçgenin tüm açı ve kenarlarının birebir aynı olduğu durumları ifade ederken; benzerlik, sadece açıların eş, kenarların ise orantılı olduğu durumları açıklar. Bu özellikler, hem teorik geometride hem de günlük hayatta karşılaşılan problemlerde kullanılabilir. Köprü yapılarından mimari tasarımlara kadar birçok uygulamada üçgenlerin eşlik ve benzerlik özelliklerinden yararlanılır. Yeni müfredat, bu kavramları gerçek hayattan alınan durumlarla ilişkilendirerek, öğrencilerin analitik düşünme becerilerini geliştirmeyi ve problem çözme yeteneklerini artırmayı amaçlamaktadır.

9. Sınıf Eşlik ve Benzerlik Konu Anlatımı

4. Tema: Eşlik ve Benzerlik Testleri 9. Sınıf (2024 – 2025 Yeni Müfredat)

• Geometrik Dönüşümler Testleri 
• İki Üçgenin Eş veya Benzer Olması İçin Gerekli Olan Asgari Koşullar Testleri 
• Bir Üçgenden Hareketle Ona Benzer Üçgenler Oluşturma Testleri 
• Tales, Öklid ve Pisagor Teoremleri Testleri 
• Eşlik ve Benzerlikle İlgili Problemler Testleri 

4. Tema: Eşlik ve Benzerlik Tema Değerlendirme Testleri

9. Sınıf Eşlik ve Benzerlik Tema Değerlendirme Testi 1 Çöz

9. Sınıf Eşlik ve Benzerlik Tema Değerlendirme Testi 2 Çöz

9. Sınıf Eşlik ve Benzerlik Tema Değerlendirme Testi 3 Çöz

9. Sınıf Eşlik ve Benzerlik Tema Değerlendirme Testi 4 Çöz

9. Sınıf Eşlik ve Benzerlik Tema Değerlendirme Testi 5 Çöz

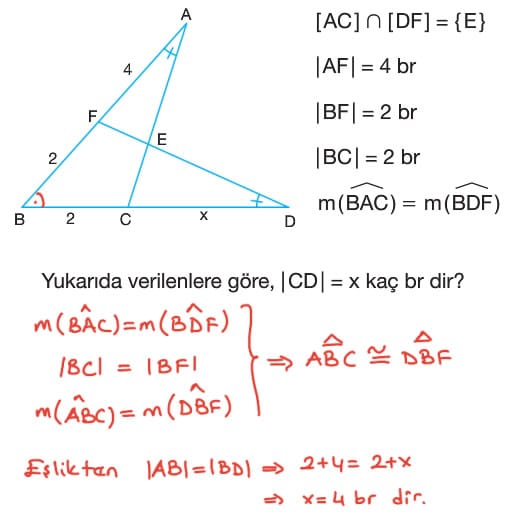
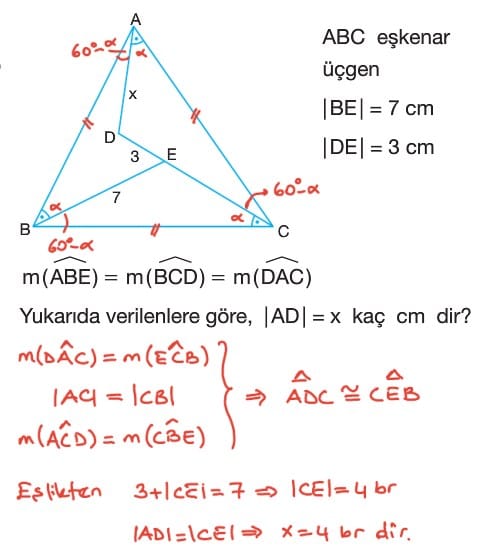
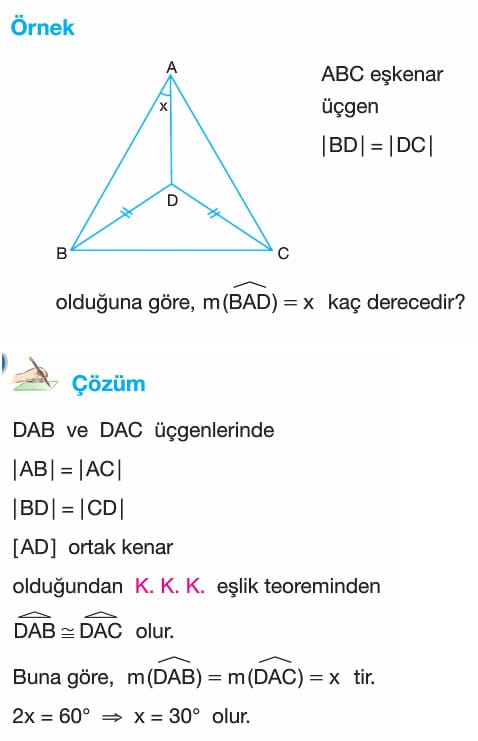
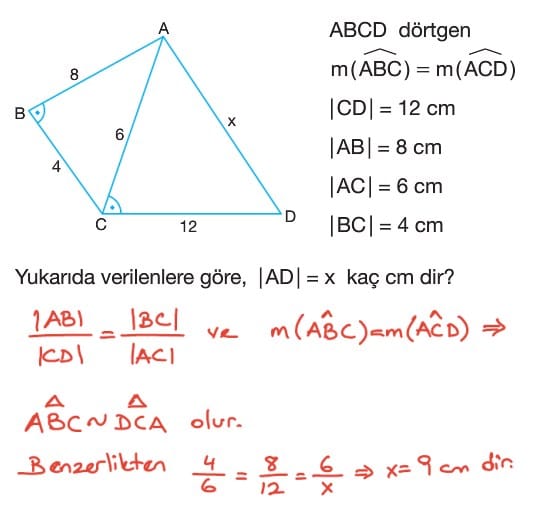
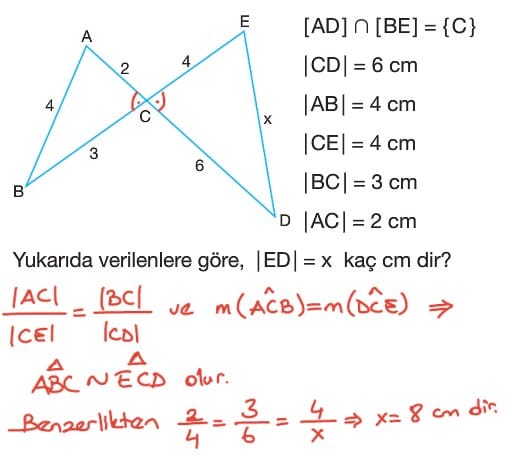
Üçgenlerde Eşlik Çözümlü Sorular

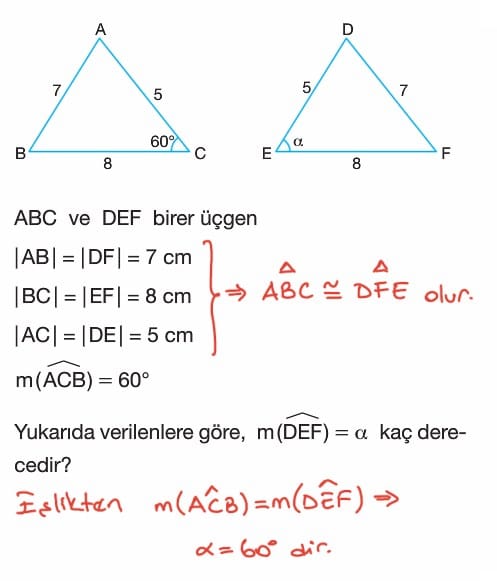
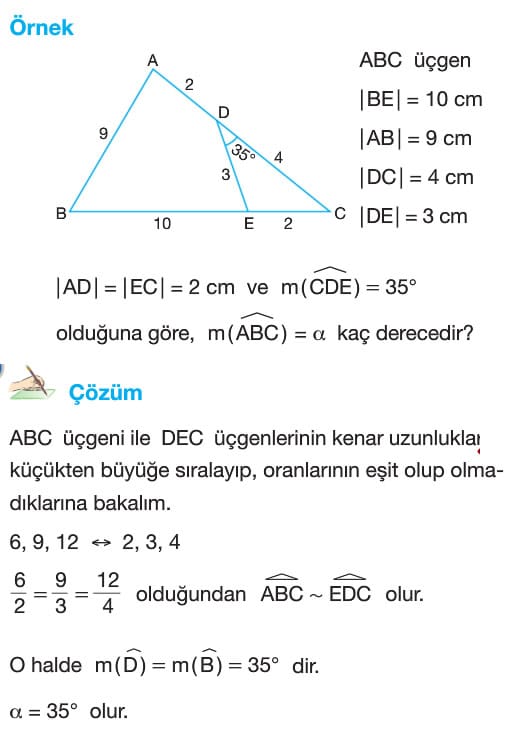
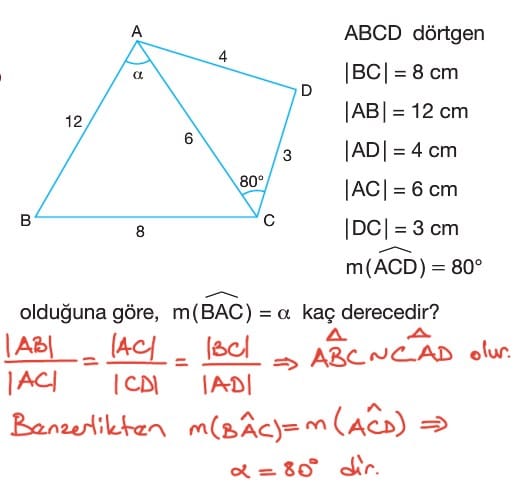
Üçgenlerde Benzerlik Çözümlü Sorular

Çözümlü Örnek Test Soruları

Soru 1

İki üçgenin kenar uzunlukları sırasıyla 3, 4, 5 ve 6, 8, 10 olarak verilmiştir. Bu üçgenler arasında hangi benzerlik bağı vardır?

A) AA (Açı-Açı) benzerlik
B) SSS (Kenar-Kenar-Kenar) benzerlik
C) SAS (Kenar-Açı-Kenar) benzerlik
D) Kenar uzunlukları eşit değil, benzerlik yok
E) Eşlik

Çözüm:

İki üçgenin benzer olması için kenarları orantılı olmalıdır. Oran: 3/6 = 4/8 = 5/10 = 1/2. Bu durumda üçgenler SSS benzerliğe göre benzerdir.

Cevap: B

Soru 2

Bir üçgende bir iç açının ölçüsü 60 derece, bir diğer açının ölçüsü ise 80 derece olarak verilmiştir. İkinci bir üçgende ise bir iç açı 60 derece ve bir diğer açı 80 derece ise bu iki üçgen arasındaki ilişki nedir?

A) Benzer
B) Eş
C) Birbirinden farklı
D) Kenar uzunlukları eşit değil, benzerlik yok
E) Sadece açıları eşit

Çözüm:

İki üçgenin iki açısı eşit olduğunda üçgenler AA benzerliğine göre benzerdir.

Cevap: A

Soru 3

ABC üçgeninde AB = 6 cm, AC = 8 cm ve BC = 10 cm. DEF üçgeninde ise DE = 12 cm, DF = 16 cm ve EF = 20 cm. Bu iki üçgen arasındaki ilişki nedir?

A) AA benzer
B) Eş
C) SSS benzer
D) SAS benzer
E) Benzerlik yok

Çözüm:

Kenar uzunlukları sırasıyla 2 katıdır: AB/DE = AC/DF = BC/EF = 1/2. Bu durumda üçgenler SSS benzerliğe göre benzerdir.

Cevap: C

Soru 4

Bir üçgende bir kenar 8 cm, diğer kenar 6 cm ve bu kenarların oluşturduğu açının ölçüsü 45 derecedir. Aynı özelliklere sahip başka bir üçgen var ise bu iki üçgen arasında hangi ilişki vardır?

A) AA benzer
B) SSS benzer
C) SAS benzer
D) Eş
E) Farklı

Çözüm:

İki üçgenin iki kenarı ve aralarındaki açı eşit ise SAS benzerliğine göre benzerdir.

Cevap: C

Soru 5

Bir üçgende iki kenarın uzunluğu 9 cm ve 12 cm olarak verilmiştir. Benzer bir üçgende bu kenarlara karşılık gelen kenarlar 3 cm ve 4 cm olduğuna göre, üçgenler arasında nasıl bir ilişki vardır?

A) Eş
B) AA benzer
C) SSS benzer
D) SAS benzer
E) Kenar uzunlukları oranında benzer

Çözüm:

9/3 = 12/4 = 3 olduğundan üçgenler SSS benzerlik koşuluna göre benzerdir.

Cevap: C

Soru 6

İki üçgen arasında AA benzerliği varsa, bu üçgenlerin alanlarının oranı nasıl bulunur?

A) Kenar uzunluklarının farkı
B) Kenar uzunluklarının oranı
C) Kenar uzunluklarının kareleri oranı
D) Kenar uzunluklarının yarısı
E) Oran yok

Çözüm:

AA benzerliğinde üçgenlerin benzerlik oranının karesi, alanlarının oranını verir.

Cevap: C

Soru 7

İki eş üçgen arasındaki fark nedir?

A) Kenar uzunlukları eşit, açıları eşit değil
B) Açıları eşit, kenar uzunlukları farklı
C) Hem açıları hem kenar uzunlukları eşit
D) Sadece alanları eşit
E) Eşkenar ve ikizkenar olmaları farkıdır

Çözüm:

Eş üçgenlerde hem kenar uzunlukları hem de açı ölçüleri eşittir.

Cevap: C

Soru 8

Bir dik üçgenin dik kenar uzunlukları 5 cm ve 12 cm olarak verilmiştir. Bu üçgene benzer bir üçgenin hipotenüsü 26 cm ise, bu üçgenin en kısa kenar uzunluğu kaç cm olur?

A) 10
B) 8
C) 5
D) 6
E) 12

Çözüm:

Öncelikle verilen dik üçgenin hipotenüs uzunluğunu bulalım: 5² + 12² = 169, hipotenüs = 13 cm. Benzer üçgenin hipotenüsü 26 cm ise, oran 26/13 = 2 olur. En kısa kenar ise 5 x 2 = 10 cm’dir.

Cevap: A

Soru 9

Ahmet, bir bina maketi hazırlarken iki üçgenin eş olduğunu fark eder. Üçgenlerden birinin kenar uzunlukları 6 cm, 8 cm ve 10 cm’dir. Eş olan diğer üçgenin kenar uzunlukları nedir?
a) 3 cm, 4 cm, 5 cm
b) 6 cm, 8 cm, 10 cm
c) 9 cm, 12 cm, 15 cm
d) 12 cm, 16 cm, 20 cm
e) 15 cm, 20 cm, 25 cm

Çözüm:
Eş üçgenlerde kenarlar birebir aynıdır. Bu nedenle diğer üçgenin kenar uzunlukları da 6 cm, 8 cm ve 10 cm olmalıdır.
Cevap: b) 6 cm, 8 cm, 10 cm

Soru 10

2. Soru
Bir üçgenin açıları 30°, 60° ve 90°’dir. Benzer bir üçgende, en kısa kenarın uzunluğu 5 cm ise, diğer kenarların uzunlukları nedir?
a) 10 cm ve 15 cm
b) 8 cm ve 12 cm
c) 5√3 cm ve 10 cm
d) 5 cm ve 5√3 cm
e) 6 cm ve 10 cm

Çözüm:
30°-60°-90° üçgeninde, kısa kenar $x$, uzun kenar $x\surd 3$, hipotenüs $2x$ olur.
x = 5 olduğundan:
Uzun kenar = 5√3
Hipotenüs = 10
Cevap: c) 5√3 cm ve 10 cm