ÇÖZÜMLÜ TEST SORULARI

Soru 1: İkizkenar Üçgende Açı Hesaplama

Bir ikizkenar üçgende taban açılarından biri 40° dir. Buna göre tepe açısı kaç derecedir?

A) 80°
B) 90°
C) 100°
D) 110°

Çözüm:

• İkizkenar üçgende taban açıları eşittir → İkinci taban açısı = 40°

• İç açılar toplamı: 180° – (40° + 40°) = 100°

Doğru Cevap: C) 100°

Soru 2: Dik Üçgende Hipotenüs Hesaplama

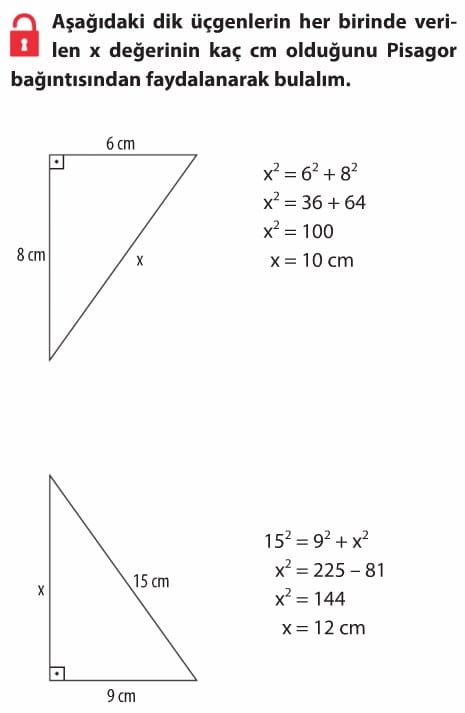
Dik kenarları 6 cm ve 8 cm olan bir dik üçgenin hipotenüsü kaç cm’dir?

A) 9
B) 10
C) 12
D) 14

Çözüm:

• Pisagor teoremi: 6² + 8² = 36 + 64 = 100

• Hipotenüs = √100 = 10 cm

Doğru Cevap: B) 10

Soru 3: Eşkenar Üçgenin Çevresi

Bir kenarı 5 cm olan eşkenar üçgenin çevresi kaç cm’dir?

A) 10
B) 15
C) 20
D) 25

Çözüm:

• Eşkenar üçgende çevre = 3 × bir kenar = 3 × 5 = 15 cm

Doğru Cevap: B) 15

Soru 4: Üçgende Açı Hesaplama

Bir üçgende iki açı 55° ve 65° olduğuna göre, üçüncü açı kaç derecedir?

A) 50°
B) 60°
C) 70°
D) 80°

Çözüm:

• Üçüncü açı = 180° – (55° + 65°) = 60°

Doğru Cevap: B) 60°

Soru 5: Üçgende Kenar-Açı İlişkisi

Bir üçgende en büyük açı hangi kenarın karşısındadır?

A) En kısa kenar
B) Orta uzunluktaki kenar
C) En uzun kenar
D) Hipotenüs

Çözüm:

• Bir üçgende en büyük açı, en uzun kenarın karşısındadır.

Doğru Cevap: C) En uzun kenar

Soru 6: Üçgenin Alanı

Taban uzunluğu 12 cm ve yüksekliği 5 cm olan bir üçgenin alanı kaç cm²’dir?

A) 30
B) 45
C) 60
D) 75

Çözüm:

• Alan = (Taban × Yükseklik)/2 = (12 × 5)/2 = 30 cm²

Doğru Cevap: A) 30