Testi çözmeye başlamadan önce Üçgende Yükseklik konusu ile ilgili çözümlü sorulara bakmanızı tavsiye ederiz. Bu sorular Üçgende Yükseklik konusunu özetlemektedir.

Üçgende Yükseklik Test 1 Çöz

Üçgende Yükseklik Kenar Orta Dikme ve Diklik Merkezi Çözümlü Sorular

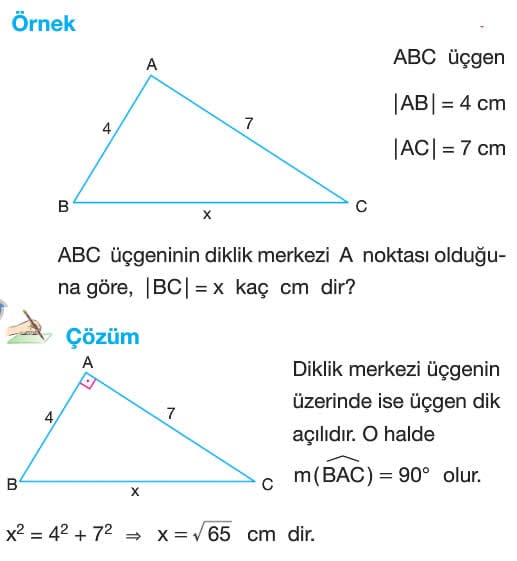
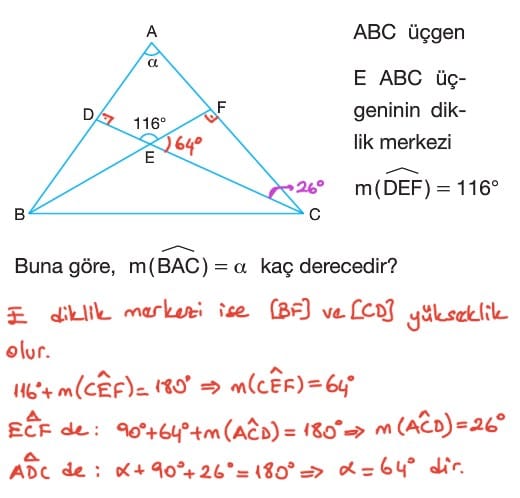
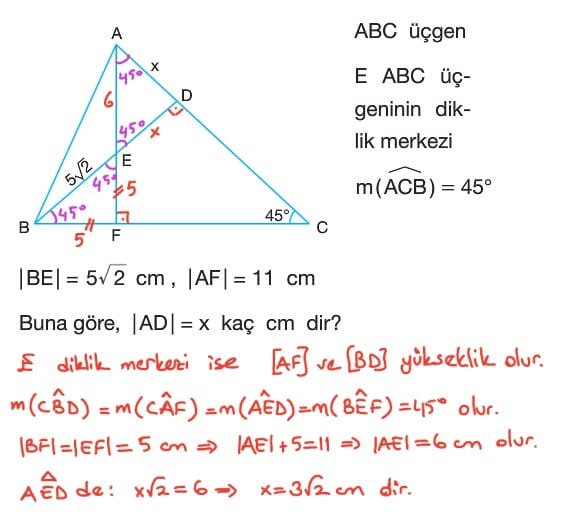
Üçgende bir köşeden karşı kenara veya kenarın uzantısına dik olarak indirilen doğru parçasına o kenara ait yükseklik denir. Yükseklikler bir noktada kesişir. Bu noktaya diklik merkezi denir. Diklik merkezi üçgenin içinde ise üçgen dar açılıdır. Diklik merkezi üçgenin üzerinde ise üçgen dik açılıdır. Diklik merkezi üçgenin dışında ise üçgen geniş açılıdır.

• Bir üçgende kenar orta dikmelerin kesim noktası üçgenin çevrel çemberinin merkezidir.
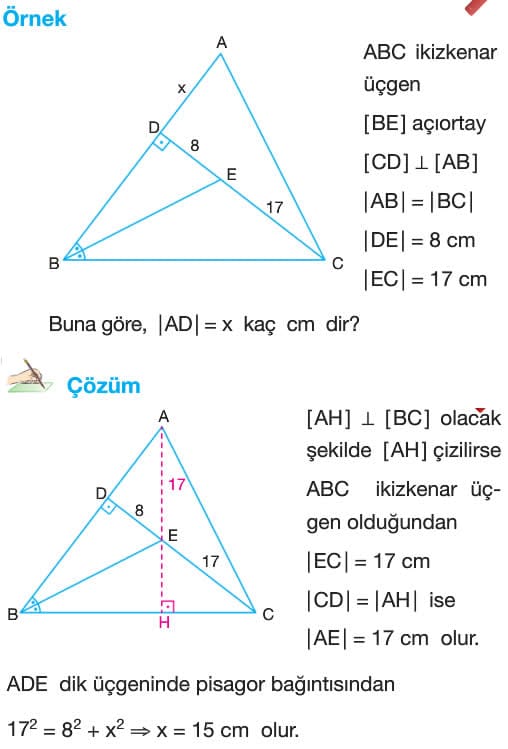
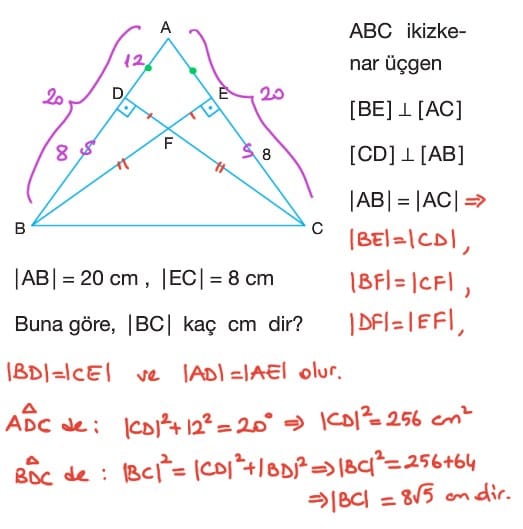
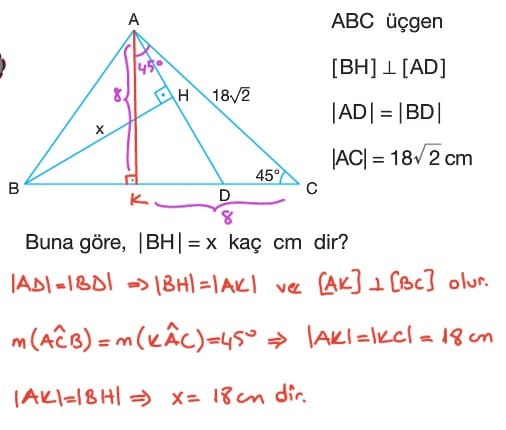
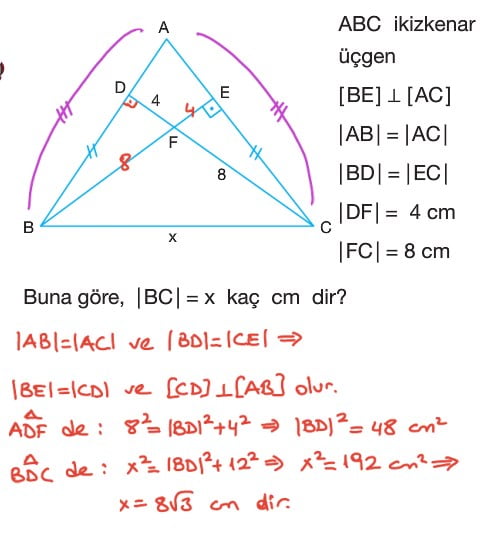
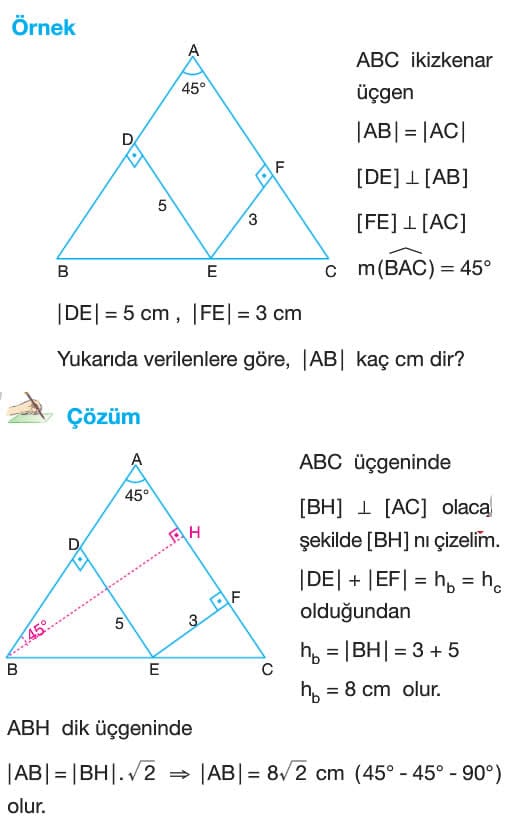
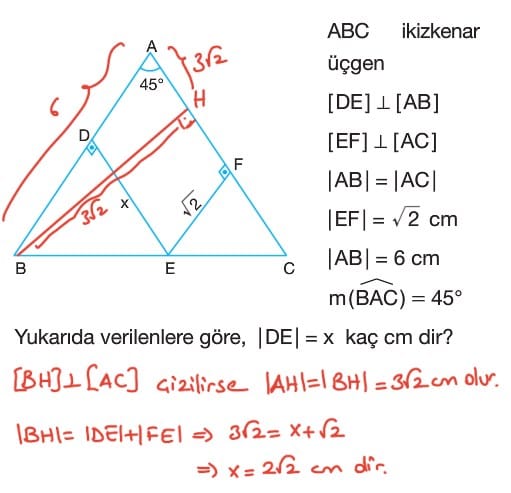
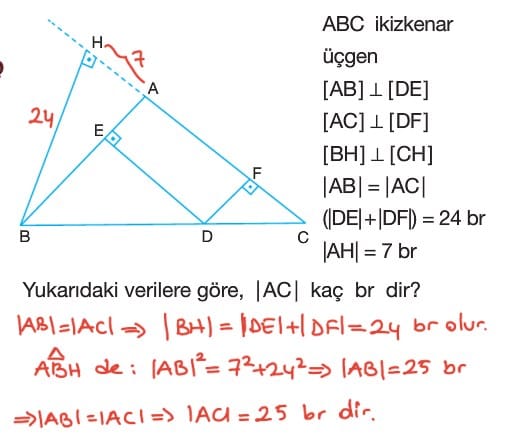
• İkizkenar üçgende, eşit olmayan kenar üzerinde alınan herhangi bir noktadan eşit kenarlara çizilen dikmelerin uzunlukları toplamı eşit kenarlara ait yüksekliğin uzunluğunu eşittir.
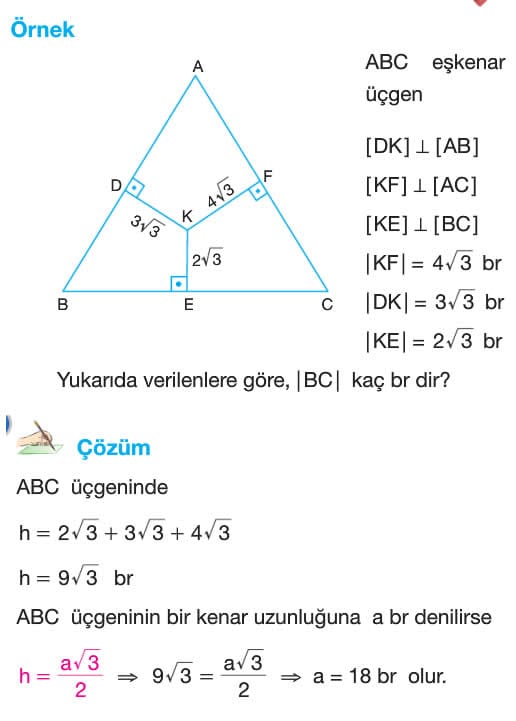
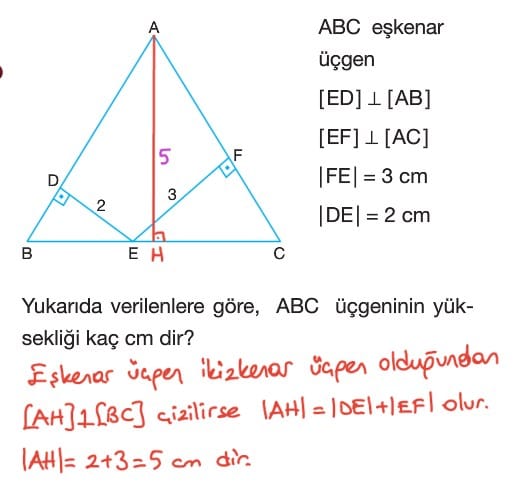
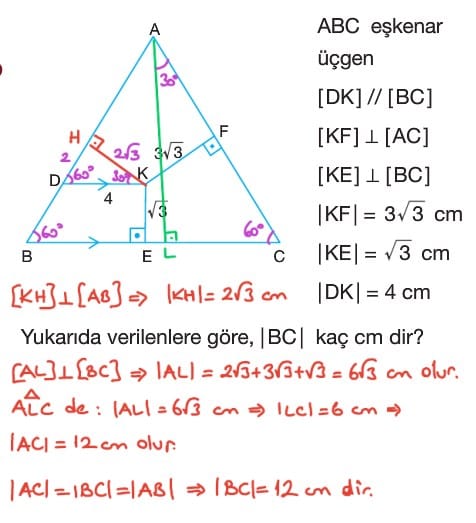
• ABC eşkenar üçgeninin iç bölgesinde alınan bir noktadan kenarlara çizilen dikmelerin uzunlukları toplamı bir yüksekliğin uzunluğuna eşittir.

Çözümlü Test Soruları

1. Dar açılı bir ABC üçgeninde diklik merkezi nerede bulunur?
A) Üçgenin dışında
B) Hipotenüs üzerinde
C) Üçgenin iç bölgesinde
D) Kenar orta noktalarında

Çözüm:
Dar açılı üçgenlerde diklik merkezi (yüksekliklerin kesişim noktası) üçgenin iç bölgesinde yer alır. Doğru cevap C‘dir.

---

2. Aşağıdaki ifadelerden hangisi yanlıştır?
A) Dik üçgende diklik merkezi dik köşeye denk gelir
B) Geniş açılı üçgende diklik merkezi üçgenin dışındadır
C) Kenar orta dikmelerin kesişimi çevrel çemberin merkezidir
D) Yükseklikler her zaman kenar orta dikmelerle çakışır

Çözüm:
Yükseklikler ile kenar orta dikmeler farklı doğrulardır, sadece eşkenar üçgende çakışırlar. Doğru cevap D‘dir.

---

3. Bir ABC üçgeninde [AH] ⊥ [BC] ve |BH| = 4 cm, |HC| = 6 cm ise, bu üçgenin diklik merkezi için ne söylenebilir?
A) [BC] kenarının üzerindedir
B) [AH] yüksekliğinin uzantısındadır
C) A köşesine denk gelir
D) Üçgenin iç bölgesindedir

Çözüm:
Verilenlerden üçgenin dar açılı olduğu anlaşılır (tüm yükseklikler iç bölgede). Diklik merkezi iç bölgede olur. Doğru cevap D‘dir.

---

4. Şekildeki O noktası ABC üçgeninin diklik merkezidir. m(BAC) = 70° ise, m(BOC) kaç derecedir?
A) 70°
B) 110°
C) 140°
D) 180°

Çözüm:
Diklik merkezinde ∠BOC = 180° – ∠A formülü uygulanır:
180° – 70° = 110°. Doğru cevap B‘dir.

---

5. Eşkenar üçgende diklik merkezi ile ilgili hangisi doğrudur?
A) Çevrel çemberin merkezinden farklıdır
B) Ağırlık merkezi ile çakışır
C) Yalnızca iki yüksekliğin kesişim noktasıdır
D) Üçgenin dışındadır

Çözüm:
Eşkenar üçgende diklik merkezi, ağırlık merkezi ve çevrel çember merkezi aynı noktadır. Doğru cevap B‘dir.

---

6. Geniş açılı bir üçgende kenar orta dikmelerin kesişim noktası (çevrel çember merkezi) için ne söylenebilir?
A) Üçgenin iç bölgesindedir
B) Hipotenüsün orta noktasıdır
C) Üçgenin dışındadır
D) Diklik merkezi ile çakışır

Çözüm:
Kenar orta dikmelerin kesişimi (çevrel çember merkezi) her üçgende iç bölgededir, diklik merkezi ise geniş açılı üçgende dışarıdadır. Doğru cevap A‘dır.