Üçgende Kenarortay, Açıortay ve Yükseklik 8. Sınıf
ÜÇGENİN YARDIMCI ELEMANLARI
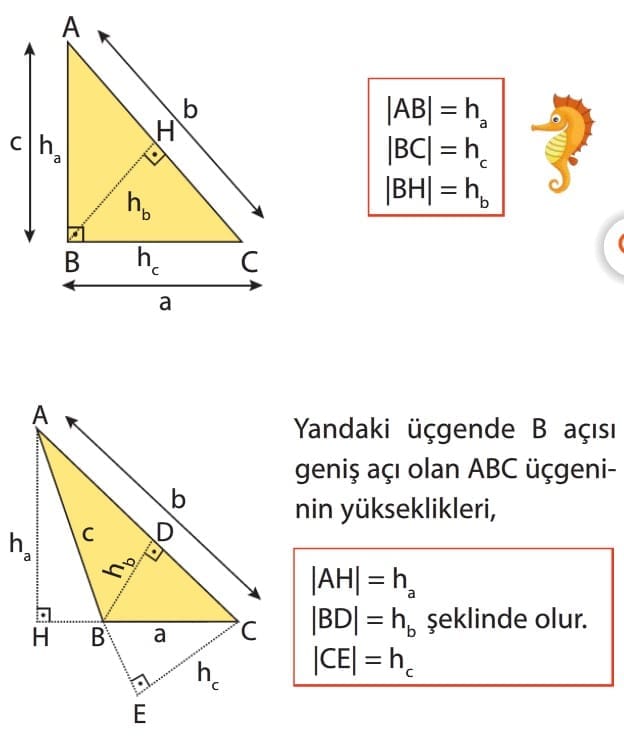
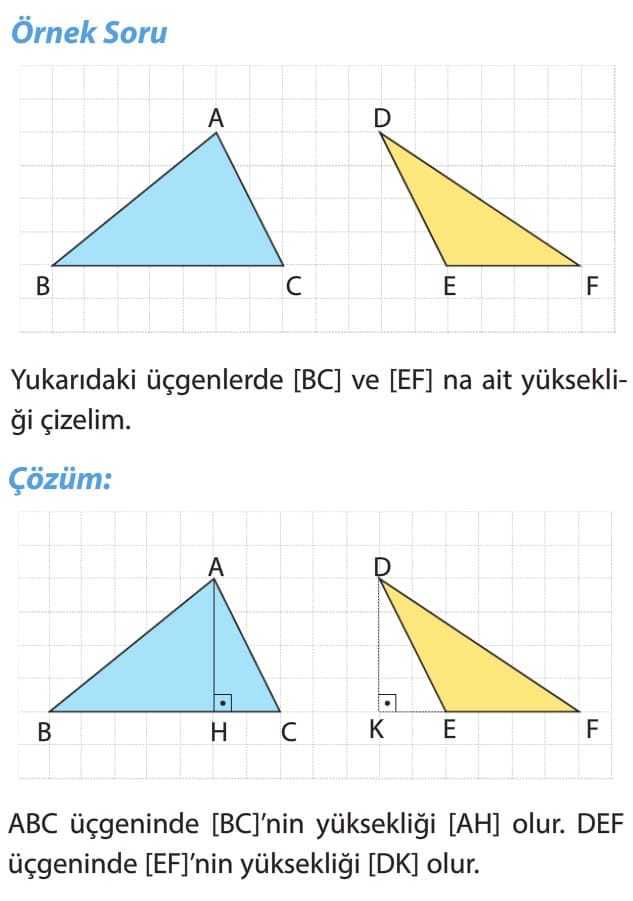
1. YÜKSEKLİK
Üçgenin bir köşesinden karşısındaki kenara veya uzantısına çizilen dik doğru parçasına o kenara ait yükseklik denir. Yüksekliklerin kesiştiği nokta üçgenin diklik merkezidir.
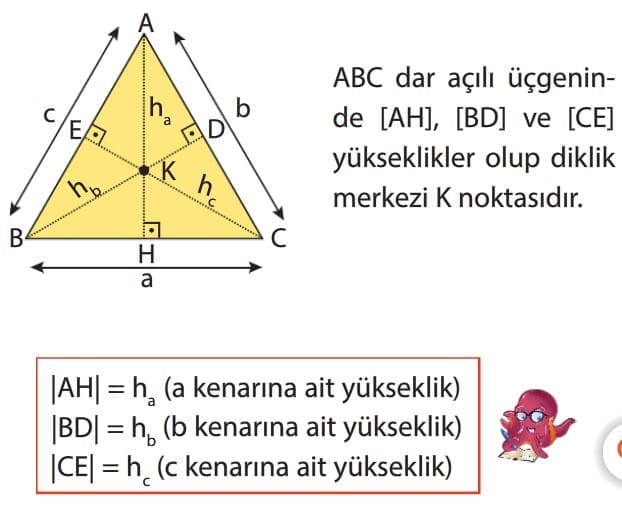
Bir dik üçgende dik kenarlar aynı zamanda yüksekliktir.
2. KENARORTAY
Üçgenin bir köşesinden karşı kenarı iki eş parçaya ayıracak şekilde çizilen doğru parçası o kenara ait kenarortaydır. Kenarortay “V” sembolü ile gösterilir. Kenarortayların kesişim noktasına üçgenin ağırlık merkezi denir ve “G” ile gösterilir.
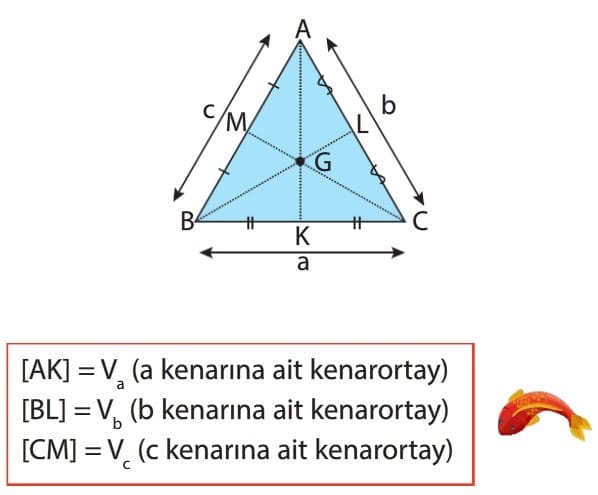
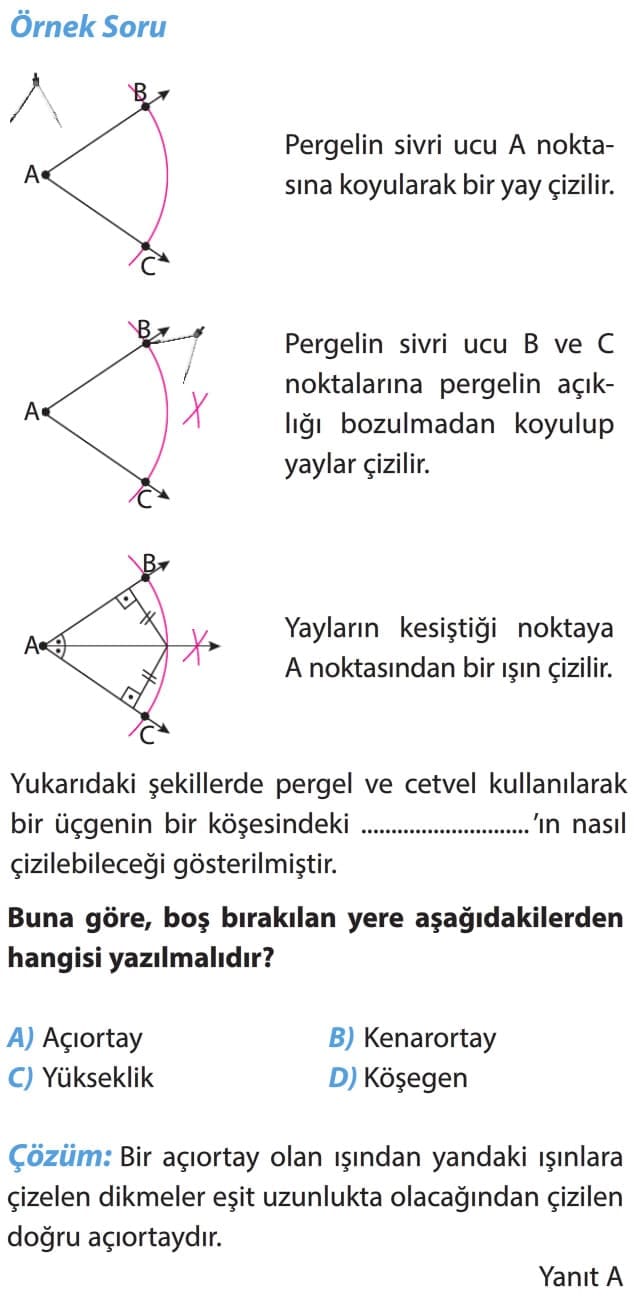
3. AÇIORTAY
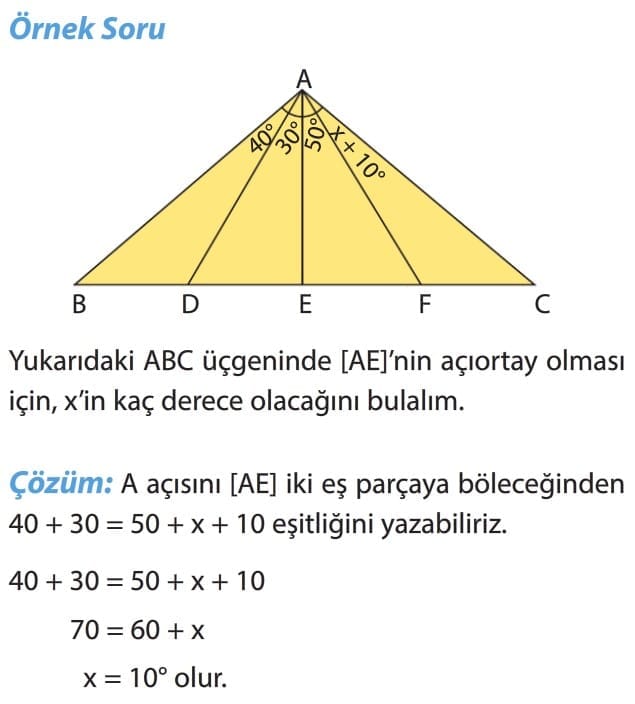
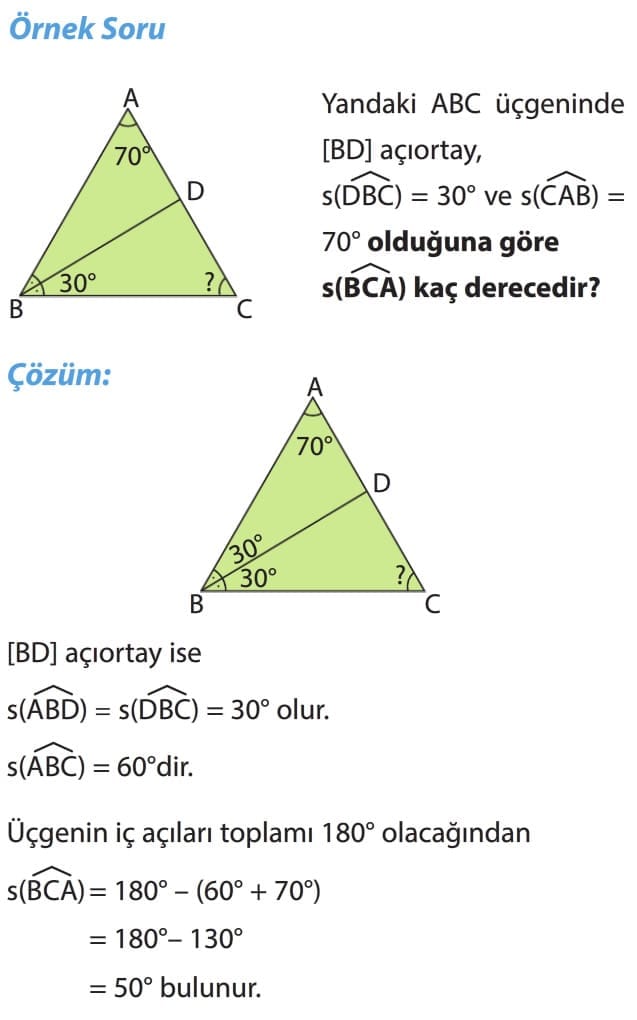
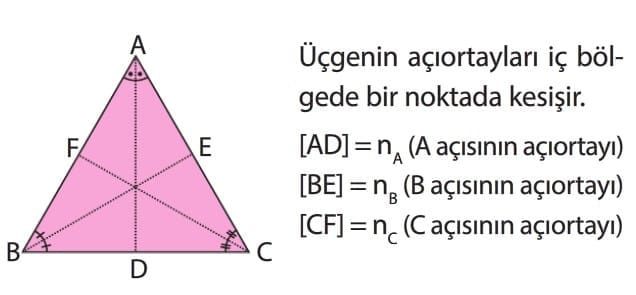
Üçgenin bir köşesindeki açıyı iki eş parçaya ayıran doğru parçasına açıortay denir. Açıortay “n” sembolü ile gösterilir.
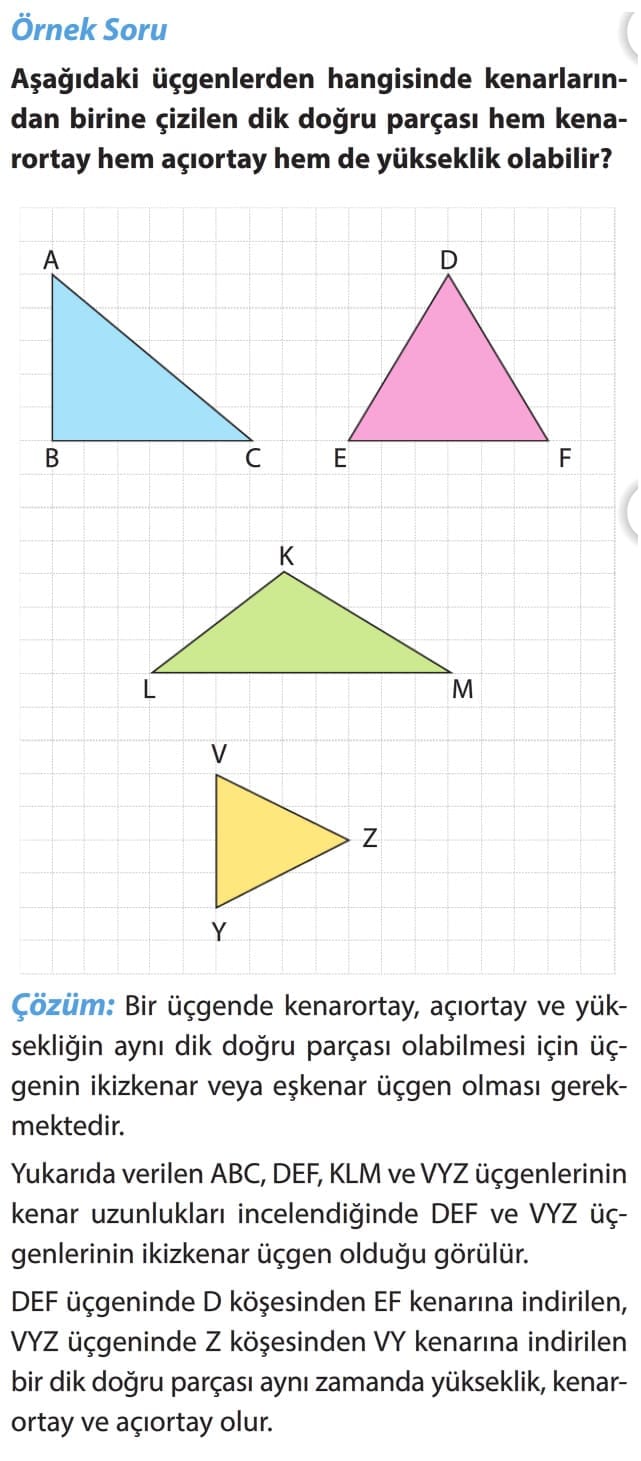
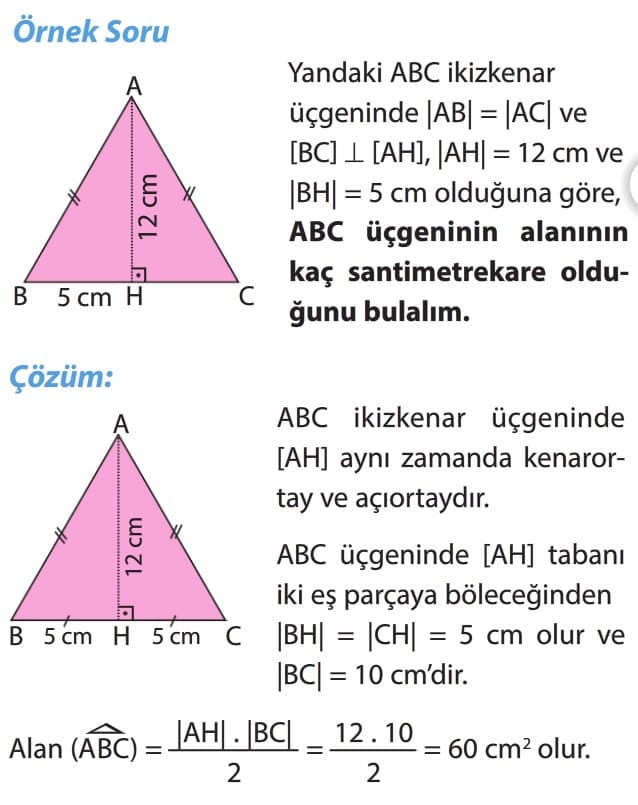
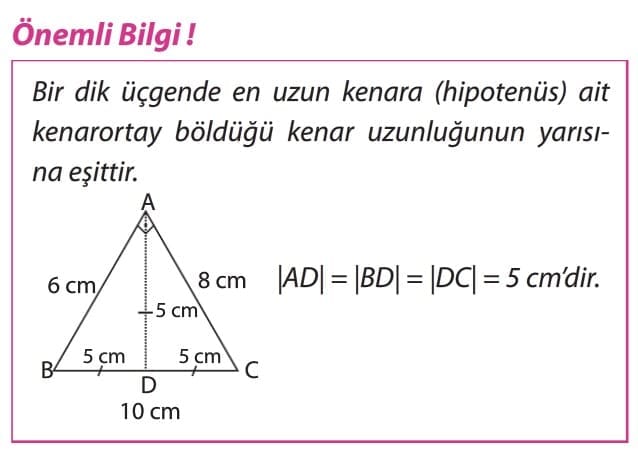
Önemli Bilgi: ikizkenar bir üçgende tabana karşısındaki köşeden indirilen dik bir doğru parçası, taban uzunluğunu iki eş parçaya ayırır. Bu dik doğru parçası aynı zamanda yükseklik, açıortay ve kenarortaydır.
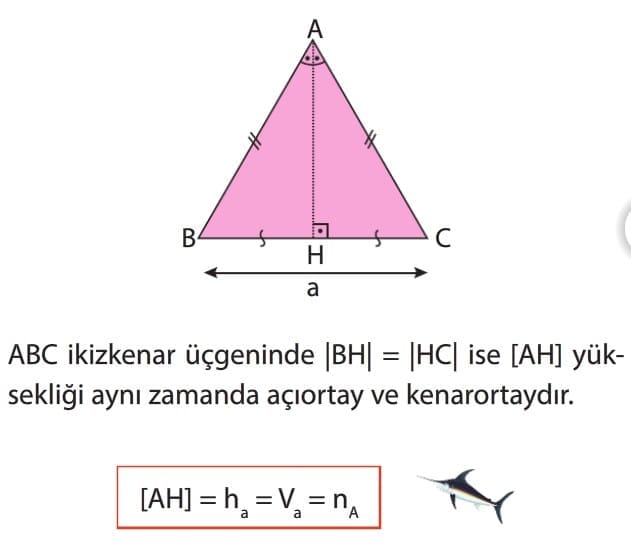
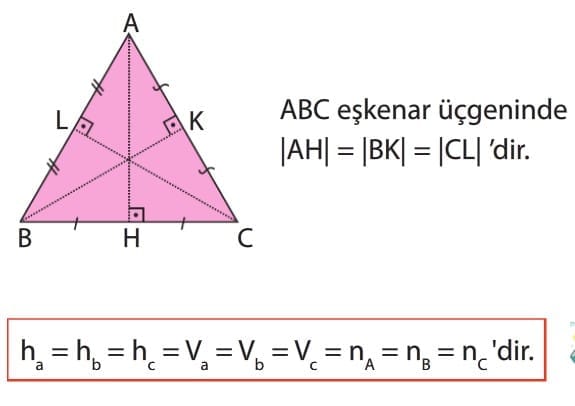
Eşkenar bir üçgende bütün yükseklikler, açıortaylar ve kenarortaylar birbirine eşit uzunluktadır.
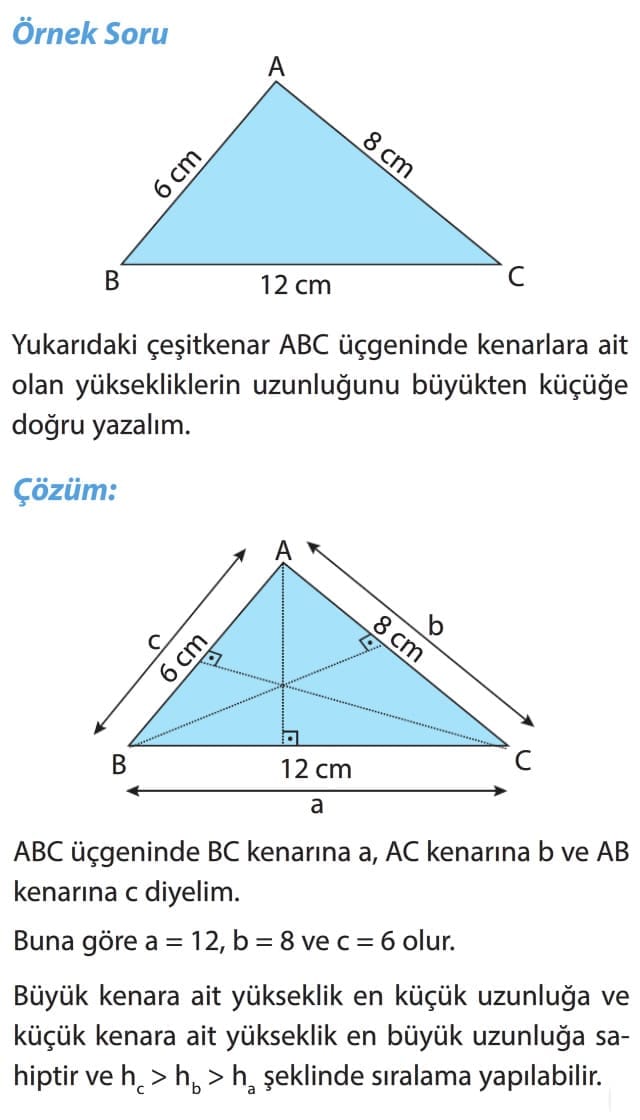
Önemli Bilgi: Bir üçgende en uzun kenara ait yükseklik, kenarortay ve bu kenara indirilen açıortay uzunluğu en küçüktür. Tam tersi olarak da en kısa kenara ait yükseklik, kenarortay ve bu kenara indirilen açıortay uzunluğu ise en büyüktür.
Önemli Bilgi: Bir çeşitkenar üçgende yardımcı elemanlardan kenarortay uzunluğu en büyük uzunluğa sahiptir. Yükseklik ise en küçük uzunlukta olup açıortay uzunluğu yükseklik ile kenarortay uzunluğu arasında bir değer alır.
Üçgende Kenarortay, Açıortay ve Yükseklik 8. Sınıf konu anlatımı Lgs Çözümlü Sorular Üçgenin Yardımcı Elemanları
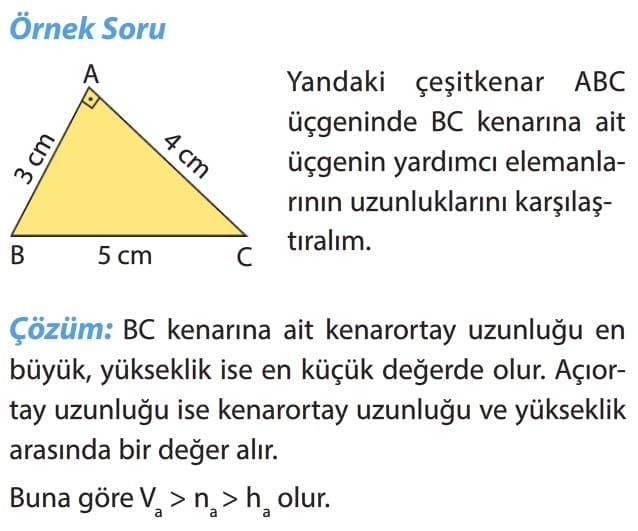
Örnek Soru: Yandaki çeşitkenar ABC üçgeninde BC kenarına ait üçgenin yardımcı elemanlarının uzunluklarını karşılaştıralım.
Çözüm: BC kenarına ait kenarortay uzunluğu en büyük, yükseklik ise en küçük değerde olur. Açıortay uzunluğu ise kenarortay uzunluğu ve yükseklik arasında bir değer alır.
Buna göre Va > na> ha olur.
Üçgenin açıortayları iç bölgede bir noktada kesişir.
[AD] = nA (A açısının açıortayı)
[BE] = nB (B açısının açıortayı)
[CF] = nc (C açısının açıortayı)
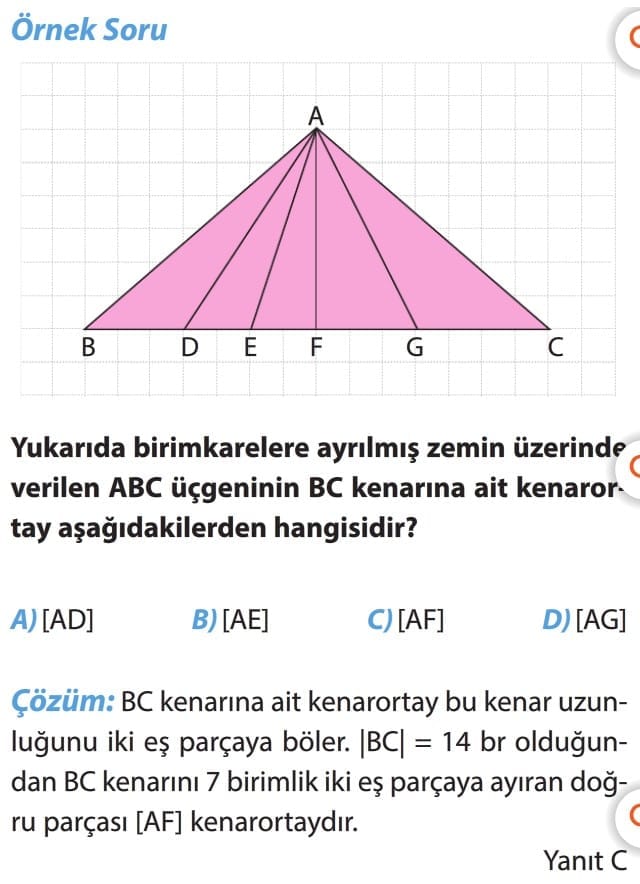
Örnek Soru: Yukarıda birim karelere ayrılmış zemin üzerinde verilen ABC üçgeninin BC kenarına ait kenarortay aşağıdakilerden hangisidir?
A) [AD] B) [AE] C) [AF] D) [AG]
Çözüm: BC kenarına ait kenarortay bu kenar uzunluğunu iki eş parçaya böler. |BC| = 14 br olduğundan BC kenarını 7 birimlik iki eş parçaya ayıran doğru parçası [AF] kenarortaydır. Yanıt C
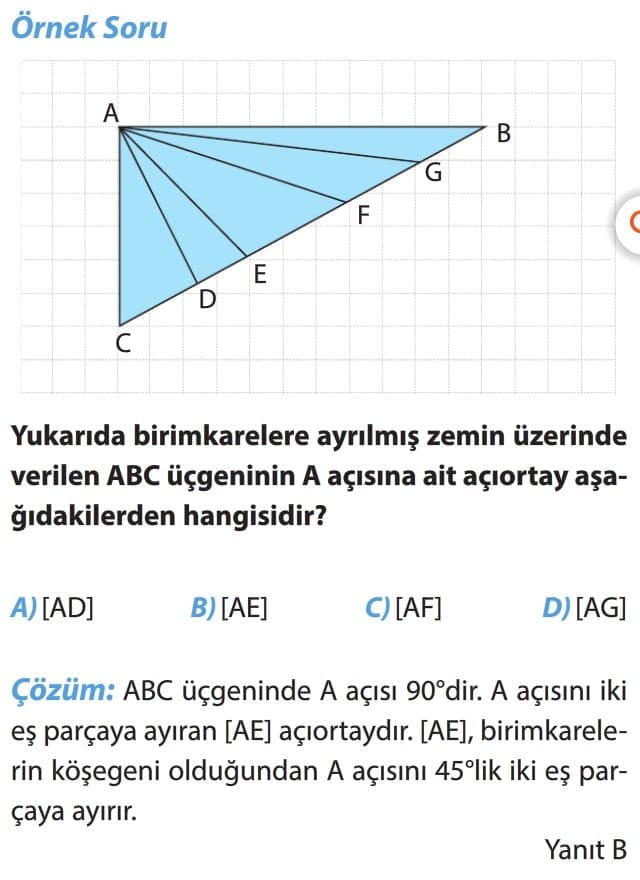
Örnek Soru: Yukarıda birim karelere ayrılmış zemin üzerinde verilen ABC üçgeninin A açısına ait açıortay aşağıdakilerden hangisidir?
A) [AD] B) [AE] C) [AF] D) [AG]
Çözüm: ABC üçgeninde A açısı 90°dir. A açısını iki eş parçaya ayıran [AE] açıortaydır. [AE], birim karelerin köşegeni olduğundan A açısını 45°lik iki eş parçaya ayırır. Yanıt B