9. Sınıf Üçgende Açıortay çözümlü sorular ve testler için bağlantıya tıklayın…

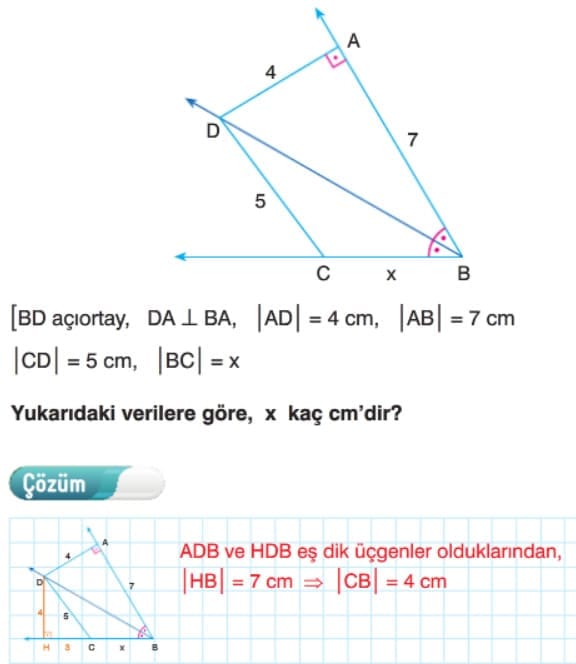
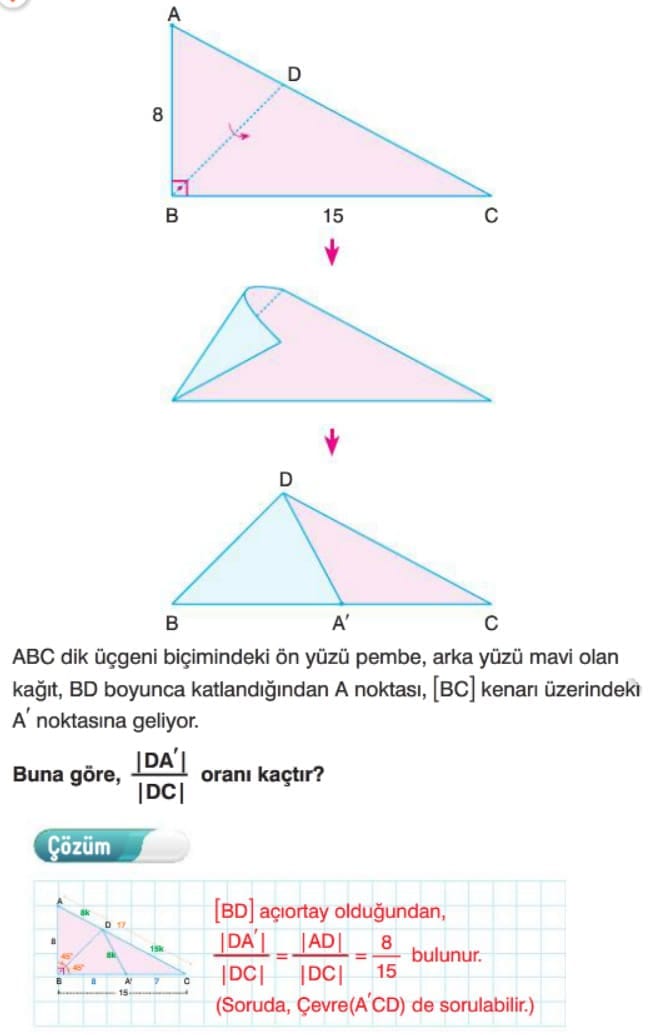
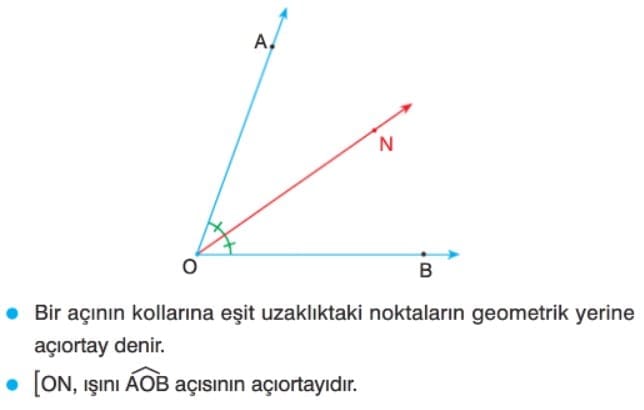
AÇIORTAY

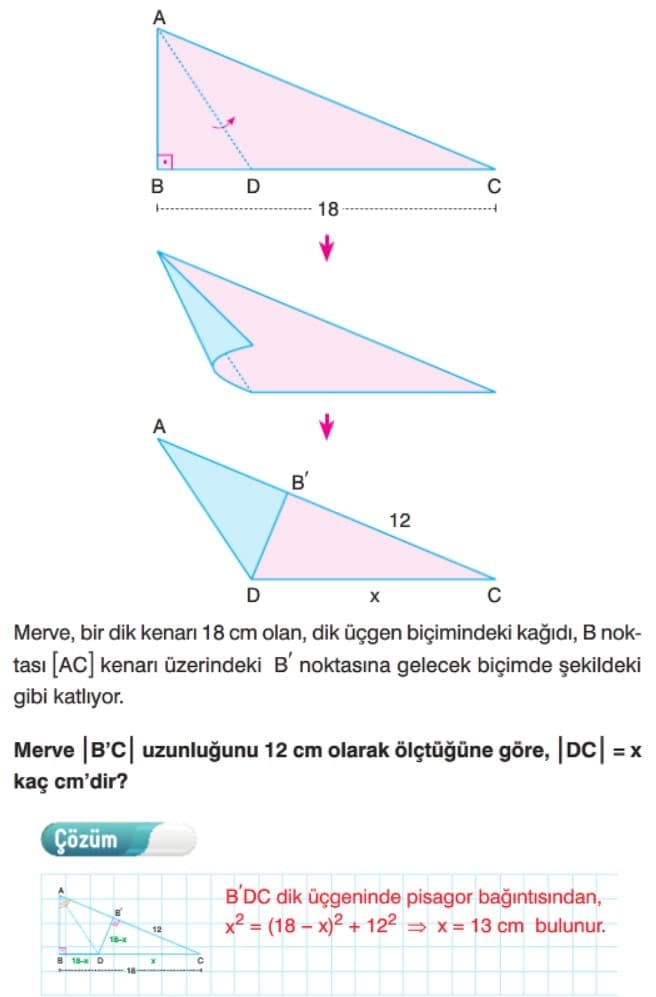
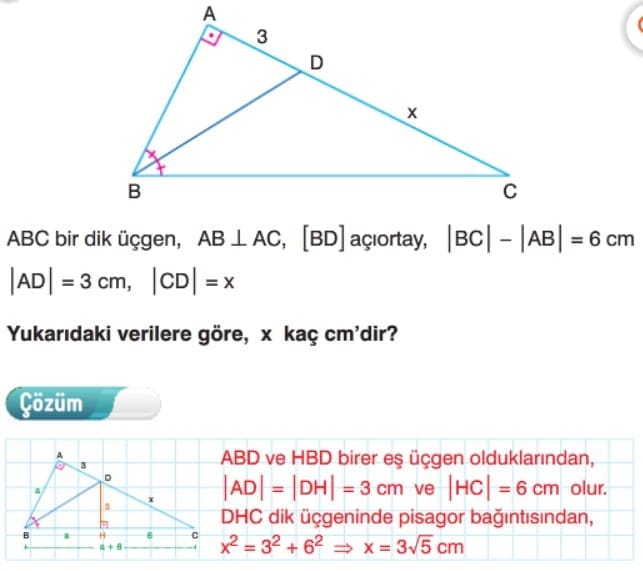
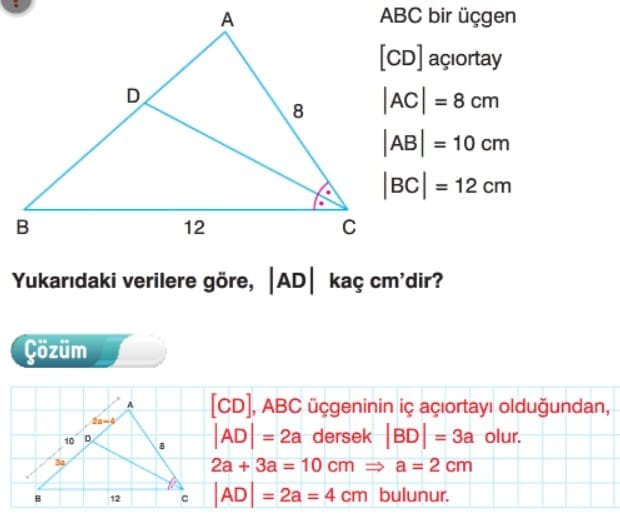
Çözümlü Sorular

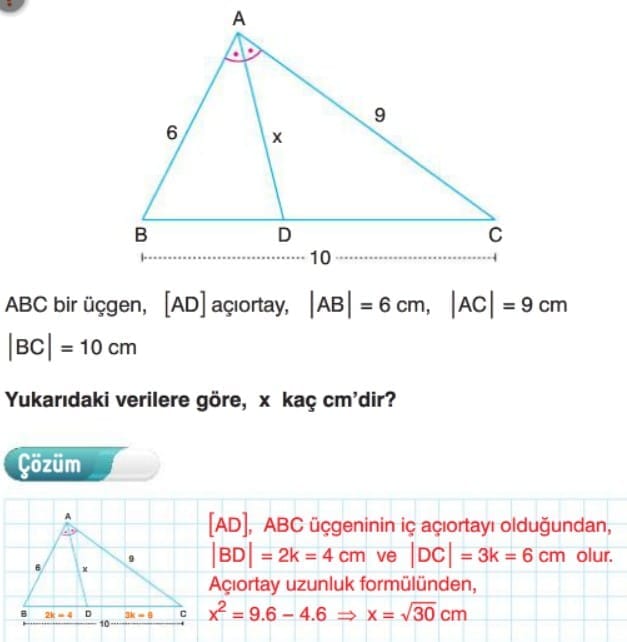
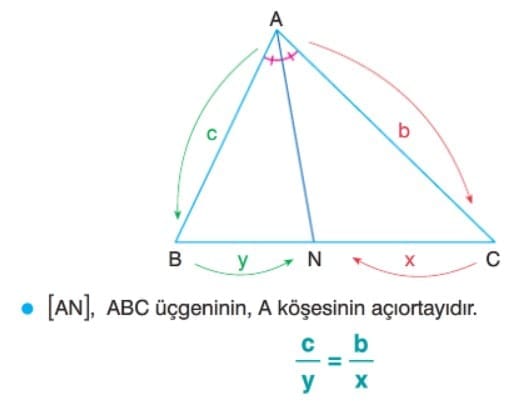
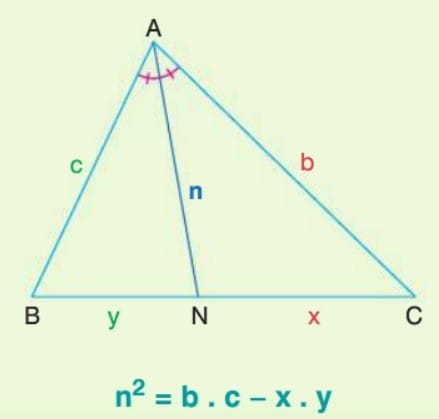
İç Açıortay Teoremi

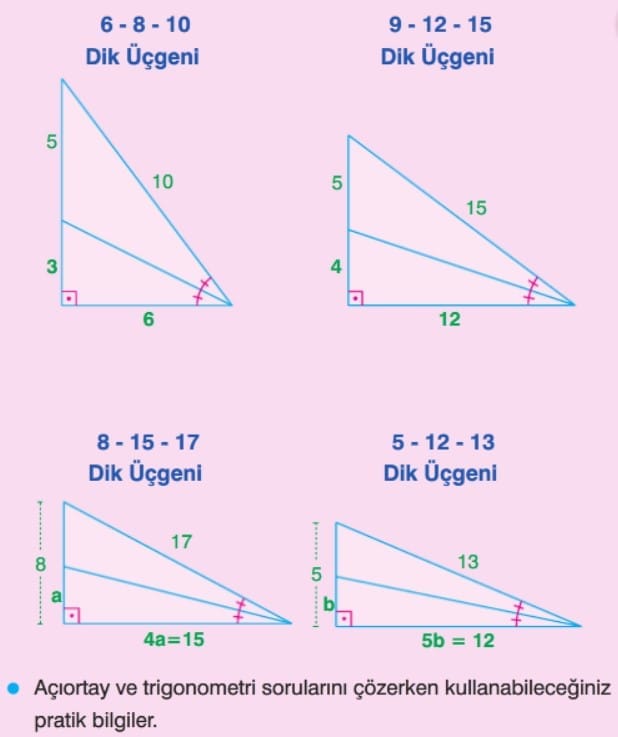
Çözümlü Sorular

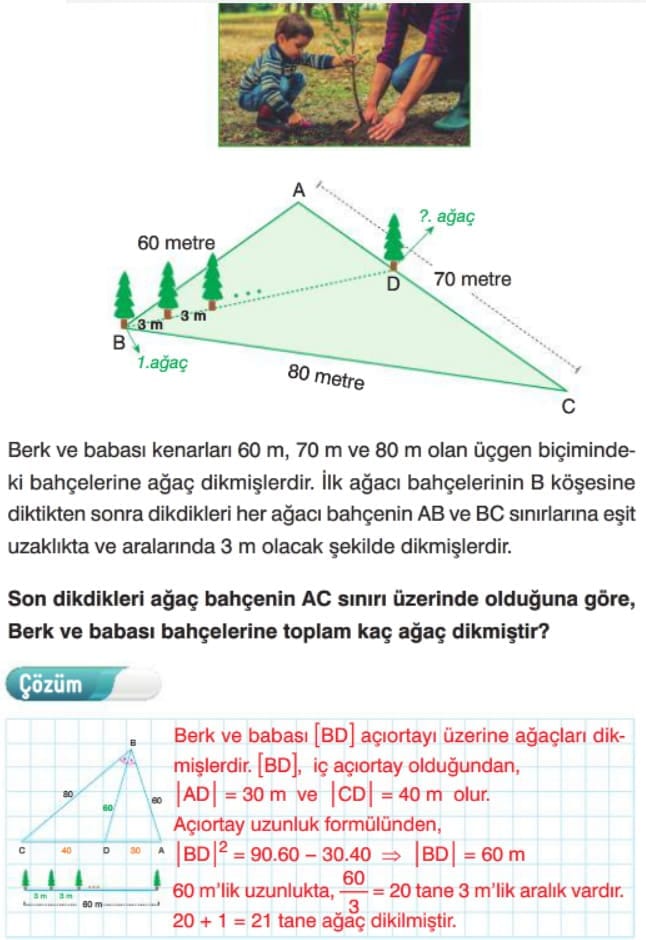
Dış Açıortay Teoremi

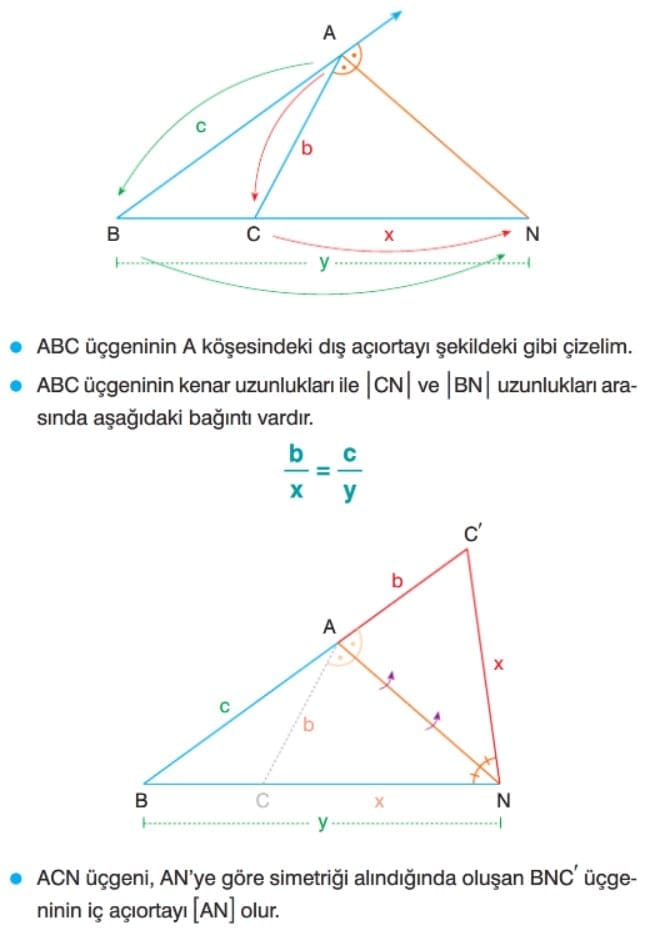
Çözümlü Sorular

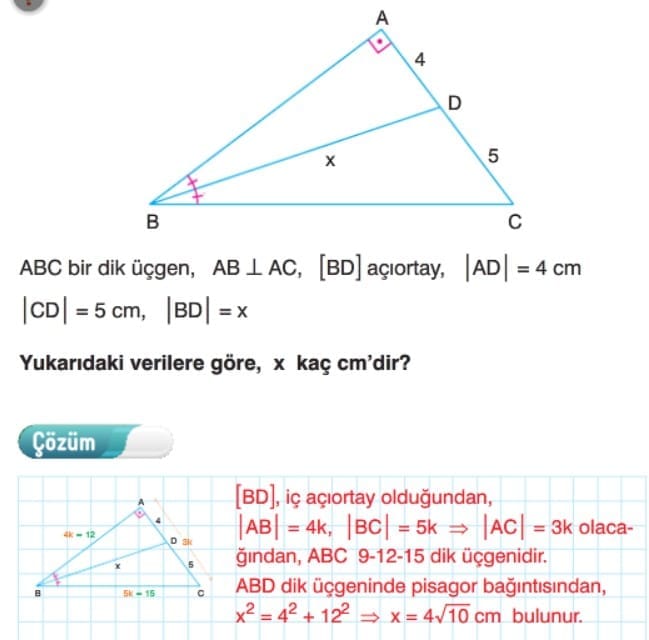
Çözümlü Örnek Test Soruları

Soru 1:
Bir üçgende, bir iç açı ortay kenarı 4 cm ve 6 cm olarak iki parçaya ayırmıştır. Bu açı ortay kenarın diğer kenarını kaç cm uzunluğundaki parçalarla böler?

A) 3 ve 7
B) 2 ve 8
C) 4 ve 6
D) 5 ve 5
E) 2 ve 10

Çözüm: Açıortay Teoremi’ne göre, bir üçgende açıortay kenarları orantılı olarak böler. Doğru cevap C şıkkıdır.

---

Soru 2:
Bir üçgende iç açının açıortayı, karşısındaki kenarı 5 ve 15 cm olacak şekilde böldüğüne göre bu üçgenin diğer kenarının uzunluğu aşağıdakilerden hangisi olabilir?

A) 10
B) 20
C) 25
D) 30
E) 35

Çözüm: Açıortay kenarları orantılı olarak böldüğü için, doğru oranlama sağlanarak doğru cevap D şıkkıdır.

---

Soru 3:
Bir üçgende açıortay, 6 cm ve 8 cm olarak ikiye böldüğü kenara karşılık gelen diğer iki kenar uzunluklarının oranı kaçtır?

A) 3/4
B) 4/5
C) 3/5
D) 5/4
E) 1/2

Çözüm: Açıortay Teoremi’ne göre, oran doğrudan bölünen kenarın iki parçasının oranıdır: 3/4, doğru cevap A şıkkıdır.

---

Soru 4:
Bir üçgende bir iç açı ortay, karşısındaki kenarı 9 ve 12 cm olacak şekilde böler. Diğer kenar uzunluklarının toplamı aşağıdakilerden hangisi olabilir?

A) 15
B) 25
C) 30
D) 35
E) 40

Çözüm: Kenar uzunlukları oranı korunarak toplam alınır. Doğru cevap C şıkkıdır.

---

Soru 5:
Bir üçgende iç açı ortay, karşısındaki kenarı 7 ve 14 cm olacak şekilde iki parçaya bölmüştür. Bu üçgenin diğer kenarının uzunluğu aşağıdakilerden hangisi olamaz?

A) 21
B) 10
C) 28
D) 14
E) 35

Çözüm: Açıortay Teoremi’ne göre orantı sağlanmadığından doğru cevap B şıkkıdır.

---

Soru 6:
Bir üçgenin bir açısını bölen açıortay, karşı kenarı 6 cm ve 18 cm olacak şekilde iki parçaya ayırıyor. Üçgenin diğer kenar uzunluğu aşağıdakilerden hangisi olabilir?

A) 12
B) 9
C) 24
D) 15
E) 20

Çözüm: Açıortay Teoremi’ne göre, bölünen parçaların oranı diğer kenarlarla orantılıdır. Doğru cevap C şıkkıdır.

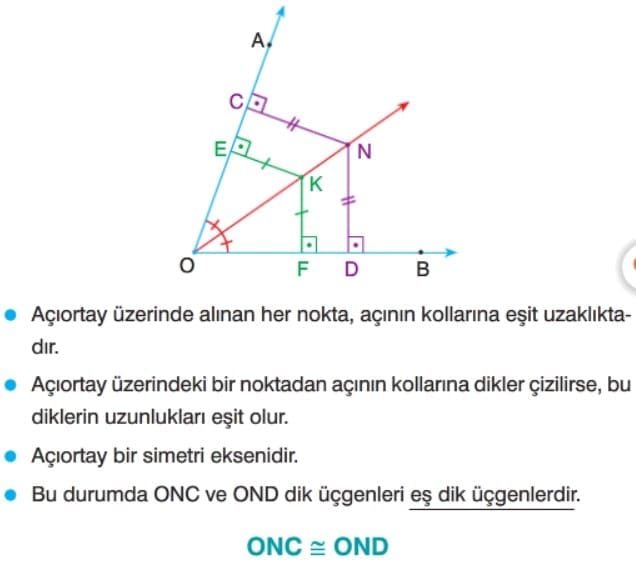
Bir açıyı iki eş açıya bölen ışına o açının açıortayı denir. Bir açının açıortayı üzerinde alınan herhangi bir noktadan açının kollarına çizilen dikmelerin uzunlukları eşittir.
Bir Açının Açıortagını Çizmek: Düzlemde A açısını oluşturan [AB ve [AC ışınları alalım. Pergelimizin sivri ucunu A noktasına koyup açının kollarını K ve L noktalarında kesen bir yay çizelim. Sonra K ve L merkezli eş yayları çizip kesişim noktasına T diyelim. Daha sonra A ve T noktalarını birleştirdiğimizde [AT ışını, A açısının açıortayı olur.

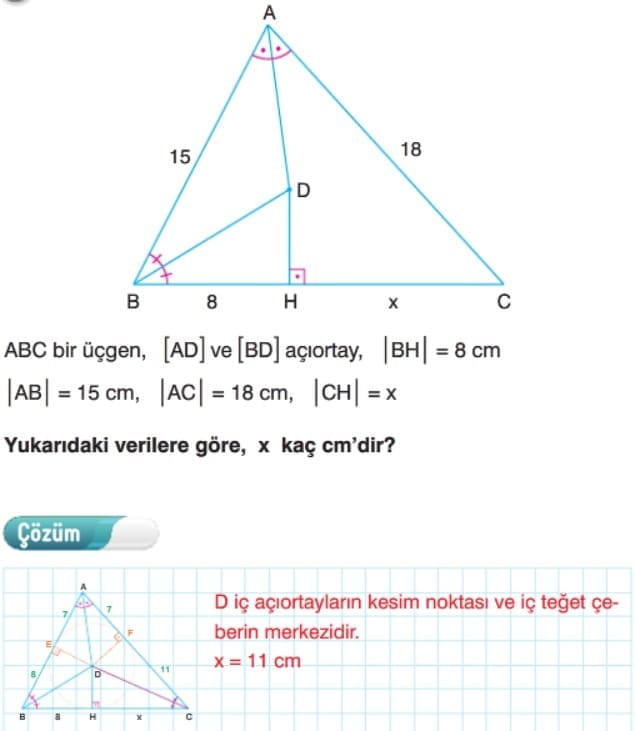
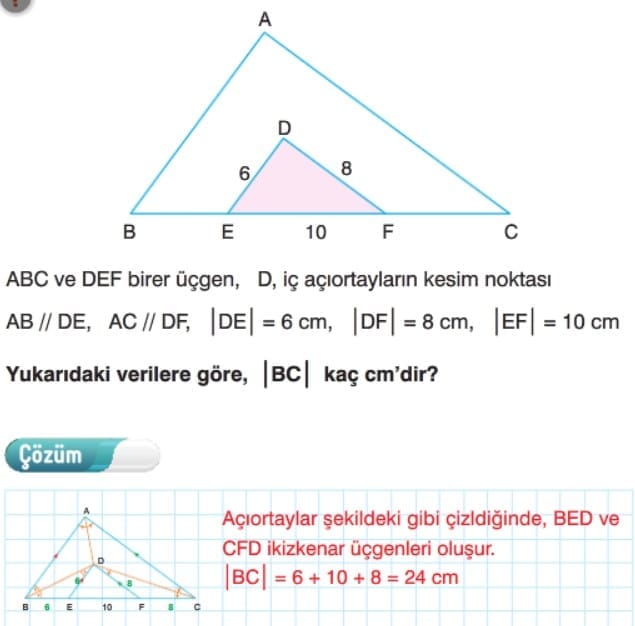
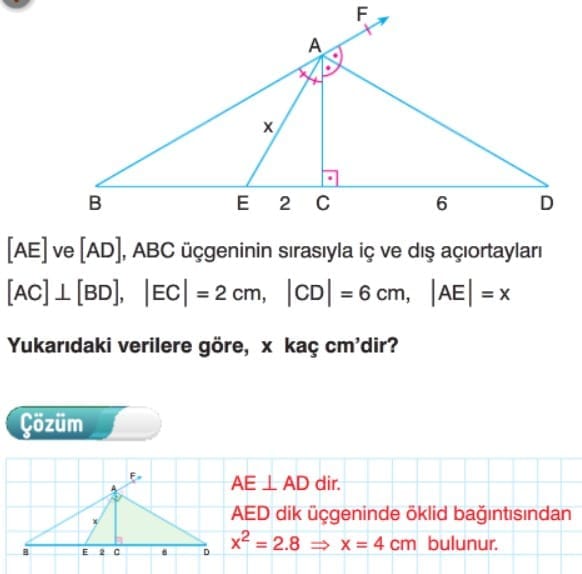
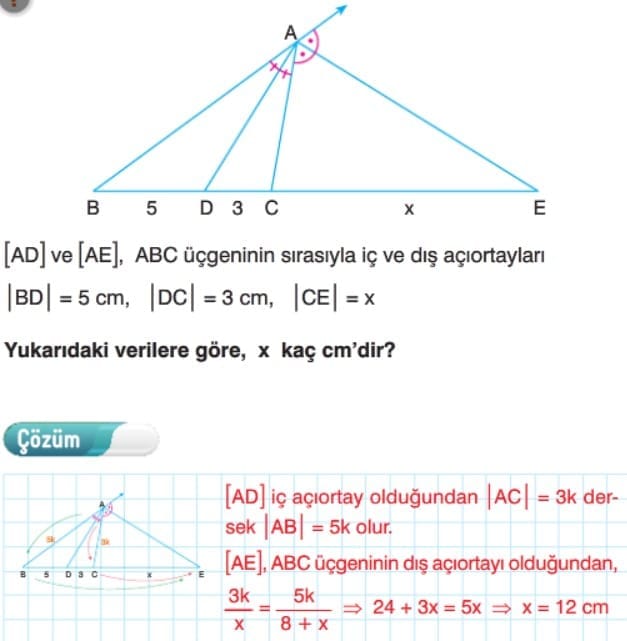
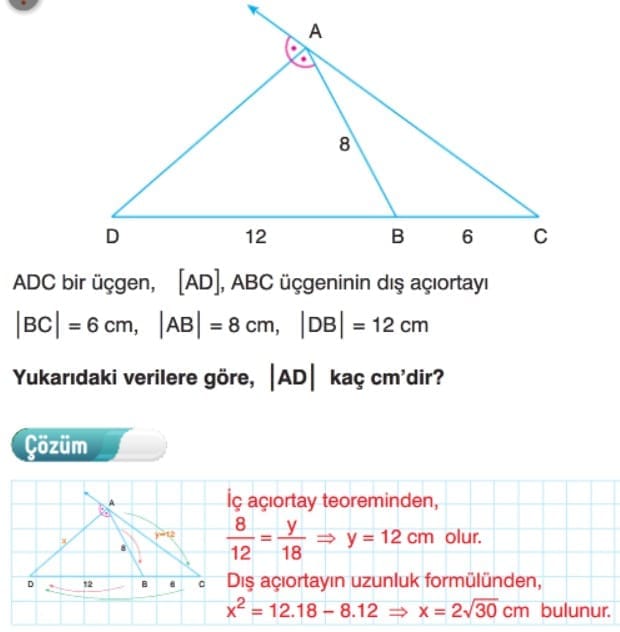
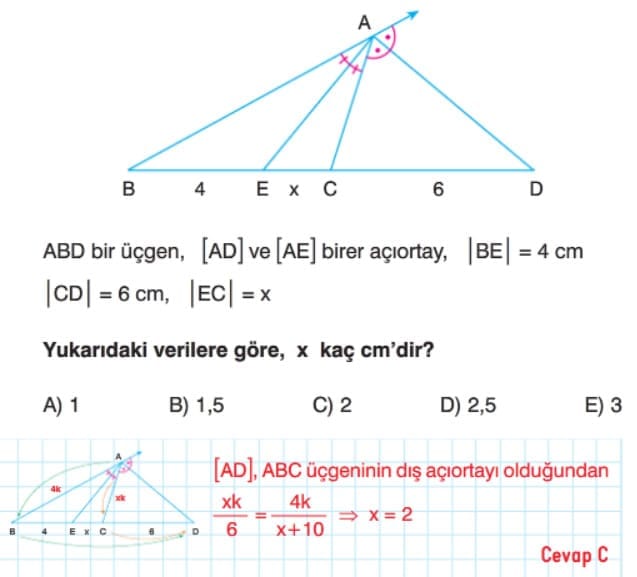
üçgende İç Açıortay Bağıntısı: Bir üçgende bir iç açıortayın karşı kenar üzerinde ayırdığı parçaların uzunlukları oranı, diğer iki kenarın uzunlukları oranına eşittir.
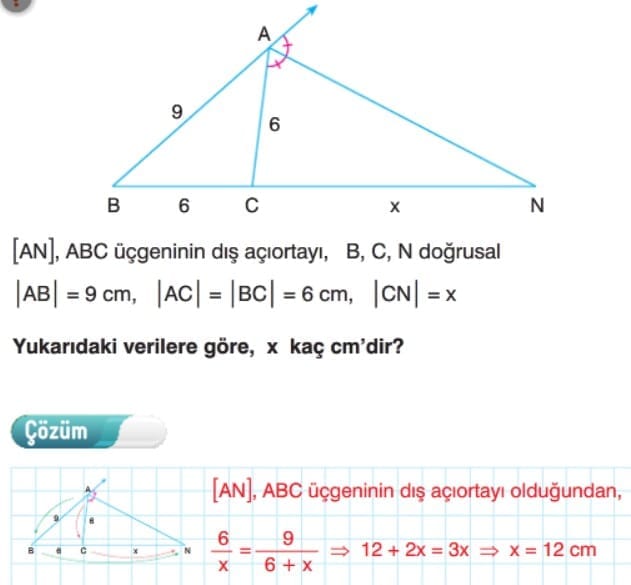
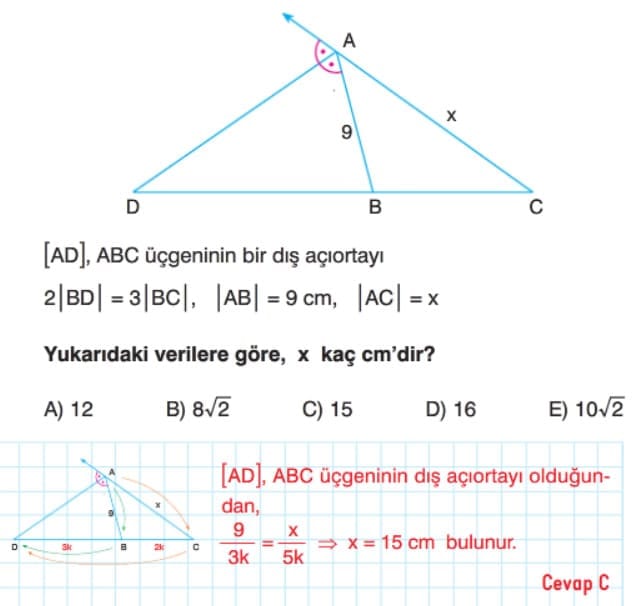
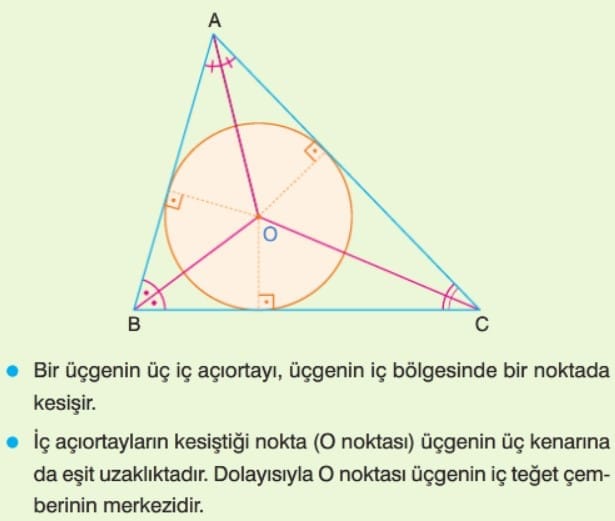
Üçgende Dış Açıortay Bağıntısı: ABC üçgeninde [AD], A köşesine ait dış açıortaydır. Bir üçgende iç açıortaylar bir noktada kesişir. Bu nokta üçgenin iç teğet çemberinin merkezidir.
Şekildeki ABC üçgeninin üç iç açıortayı 0 noktasında kesiştiğinden O noktası iç teğet çemberin merkezidir.
Şekildeki ABC üçgeninin iç teğet çemberinin merkezi olan O noktasının kenarlara olan uzaklıkları çemberin yarıçaplarıdır.

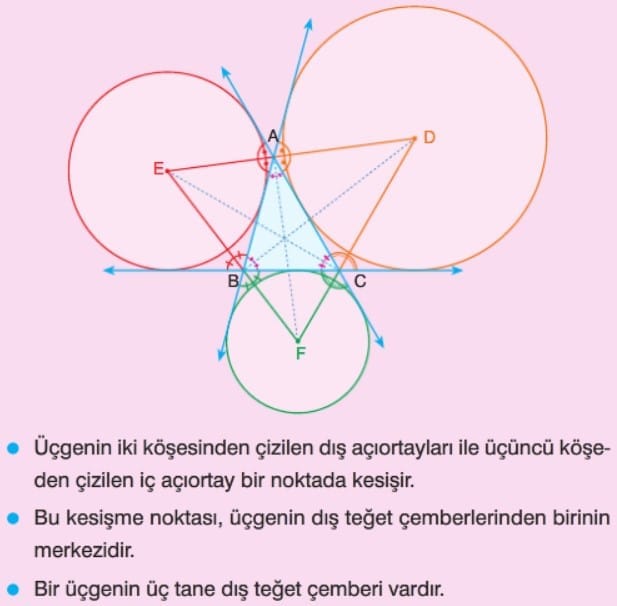
Üçgenin Dış Teğet Çemberi: Bir üçgende iki dış açıortay ile bir iç açıortayın kesim noktası üçgenin dış teğet çemberinin merkezidir. Şekildeki O noktası, [AO] ve [CO] dış açıortayları ile [BO] iç açıortayının kesim noktasıdır. Bir üçgende üç tane dış teğet çember vardır.
Çözüm: K noktası, ABC üçgeninin iç teğet çemberinin merkezi ise [AK] ve [CK] iç açıortaydır. 0 noktası, ABC üçgeninin dış teğet çemberinin merkezi olduğundan, [AO] ve [CO] dış açıortay olur. A ve C köşelerindeki açıortaylar dik kesiştiğinde m(KAO) = m(KCO) = 90° olur. [KO] çizince AKO ve KCO dik üçgenlerinde Pisagor bağıntısından kök 10 bulunur.

Açıortayın Tarihçesi: Açıortayın kullanımı ve incelenmesi geometrinin tarihine dayanmaktadır. Antik Yunan matematikçileri, özellikle Euclid, üçgenlerin özellikleri üzerine çalışmışlardır. Euclid’in “Elements” adlı eseri, geometrinin temel taşlarından biridir ve üçgenlerin özellikleri, açıortay gibi konuları içerir. Bu eser, M.Ö. 300 civarında yazılmıştır ve matematikteki temel kavramları sistemleştirmiştir.

Açıortay Uygulamaları

Üçgenin Özellikleri: Açıortay, üçgenin özellikleri üzerine birçok teorem geliştirmek için kullanılır.
Geometrik İnşa İşlemleri: Açıortay, geometrik inşa işlemlerinde kullanılır. Örneğin, belirli bir açının açıortayını çizmek.
Trigonometrik İlişkiler: Açıortay, trigonometrik hesaplamalarda kullanılabilecek açılar arası ilişkileri anlamak için de kullanılır.