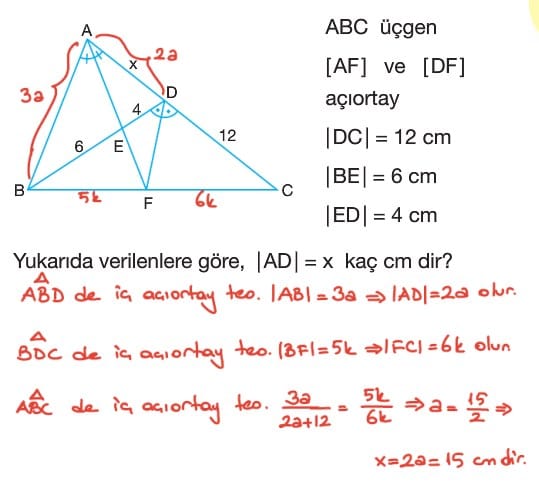
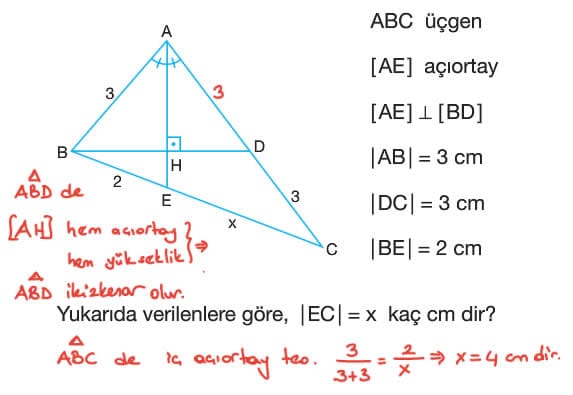
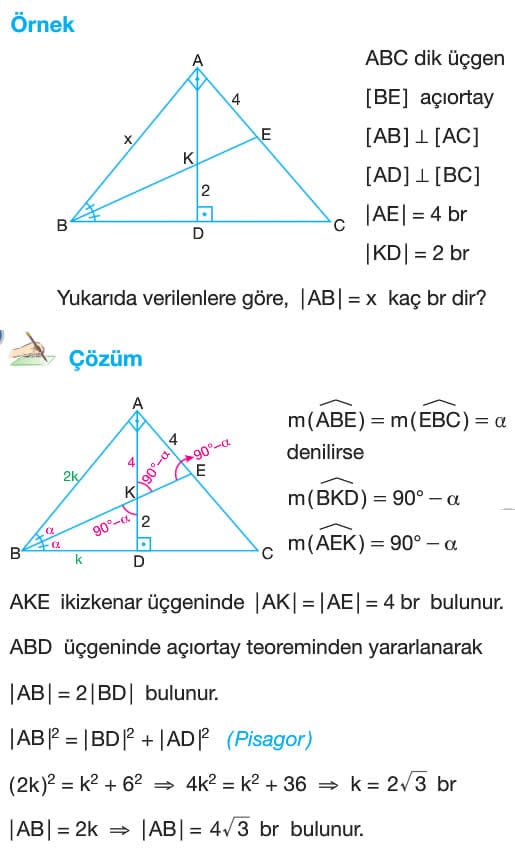
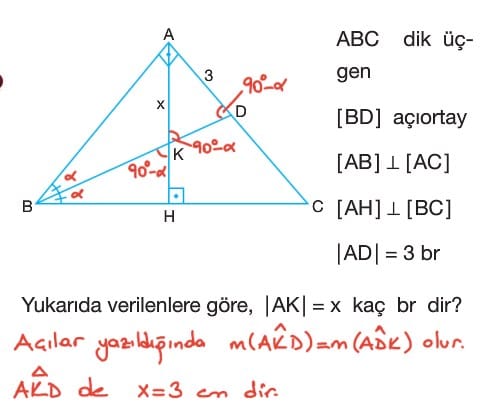
Üçgende Açıortay Test Çöz 9. Sınıf
Testlerin altında Üçgende Açıortay Çözümlü Sorular yer almaktadır. Testleri çözmeye başlamadan çözümlü sorulara bakmanızı tavsiye ederiz. Çözümlü sorular Üçgende Açıortay konusunu özetlemektedir.
Üçgende Testler
Üçgende Açıortay Test 1 Çöz
Üçgende Açıortay Çözümlü Sorular
Çözümlü Örnek Test Soruları
Soru 1
Bir üçgende, bir açının açıortayı, açıyı iki eşit parçaya böler. Eğer açının ölçüsü 70° ise, açıortayın oluşturduğu her bir açının ölçüsü kaç derece olur?
A) 30°
B) 35°
C) 40°
D) 45°
E) 50°
Çözüm:
Açıortay, açıyı iki eşit parçaya böldüğünden, 70° ÷ 2 = 35° olur.
Cevap: B
Soru 2
Bir üçgenin iç açılarından birinin ölçüsü 90° ve bu açının açıortayı çizilirse, açıortay çizilen açının her iki parçasının ölçüleri toplamı kaç derece olur?
A) 30°
B) 45°
C) 60°
D) 90°
E) 120°
Çözüm:
Açıortay, açıyı iki eşit parçaya böler. Bu durumda 90°’lik açının her iki parçasının toplamı 90° olur.
Cevap: D
Soru 3
Bir üçgenin bir açısının ölçüsü 60° ve bu açının açıortayı çizildiğinde her bir açının ölçüsü kaç derece olur?
A) 15°
B) 20°
C) 25°
D) 30°
E) 35°
Çözüm:
Açıortay, açıyı iki eşit parçaya böler. 60° ÷ 2 = 30° olur.
Cevap: D
Soru 4
Bir üçgende, bir açıortay uzunluğunun üçgenin diğer kenarına olan uzaklığı 5 cm ve bu açıortayın karşısındaki kenarın uzunluğu 10 cm ise, açıortayın üçgenin kenarlarına olan oranı kaçtır?
A) 1/2
B) 2/3
C) 3/4
D) 1/3
E) 1/4
Çözüm:
Açıortay teoremi gereği, açıortay, karşı kenarı iki orantılı parçaya böler. Bu durumda uzunluk oranı 1/2 olur.
Cevap: A
Soru 5
Bir üçgenin bir iç açısının ölçüsü 80° ve bu açıya ait açıortayın çizildiği noktada her iki parçanın toplamı kaç derecedir?
A) 30°
B) 40°
C) 50°
D) 80°
E) 100°
Çözüm:
Açıortay, açıyı iki eşit parçaya böler. Toplamları, başlangıç açısı olan 80°’dir.
Cevap: D
Soru 6
Bir üçgende bir iç açının açıortayı, karşı kenarı 12 cm ve üçgenin diğer kenarını 6 cm uzunlukta iki parçaya ayırıyorsa, açıortayın uzunluğu nedir?
A) 3 cm
B) 4 cm
C) 5 cm
D) 6 cm
E) 8 cm
Çözüm:
Açıortay teoremi gereği, karşı kenarı iki eşit uzunluklu parça halinde böler. 6 cm olduğu için, toplam uzunluk 12 cm olarak korunur.
Cevap: D
Soru 7
Bir üçgenin iç açılarından biri 120° ve bu açının açıortayı çizildiğinde her iki parçanın ölçüsü kaç derece olur?
A) 30°
B) 45°
C) 60°
D) 75°
E) 90°
Çözüm:
120°’lik açının açıortayı, açıyı iki eşit parçaya böler. Bu durumda her bir parça 120 ÷ 2 = 60° olur.
Cevap: C
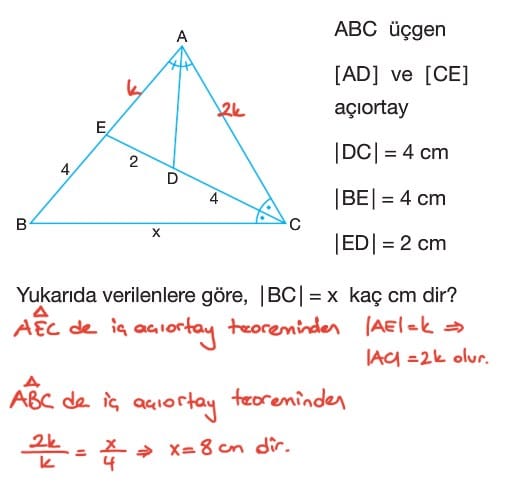
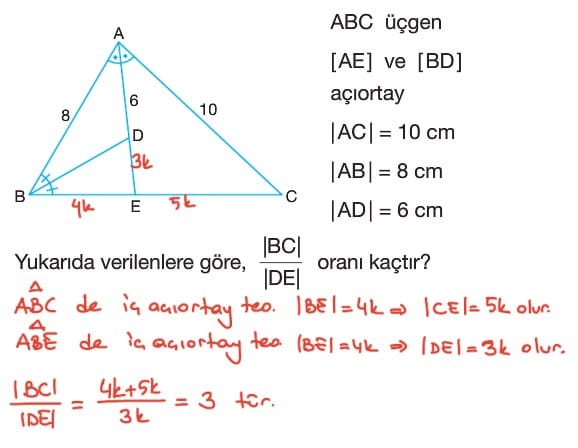
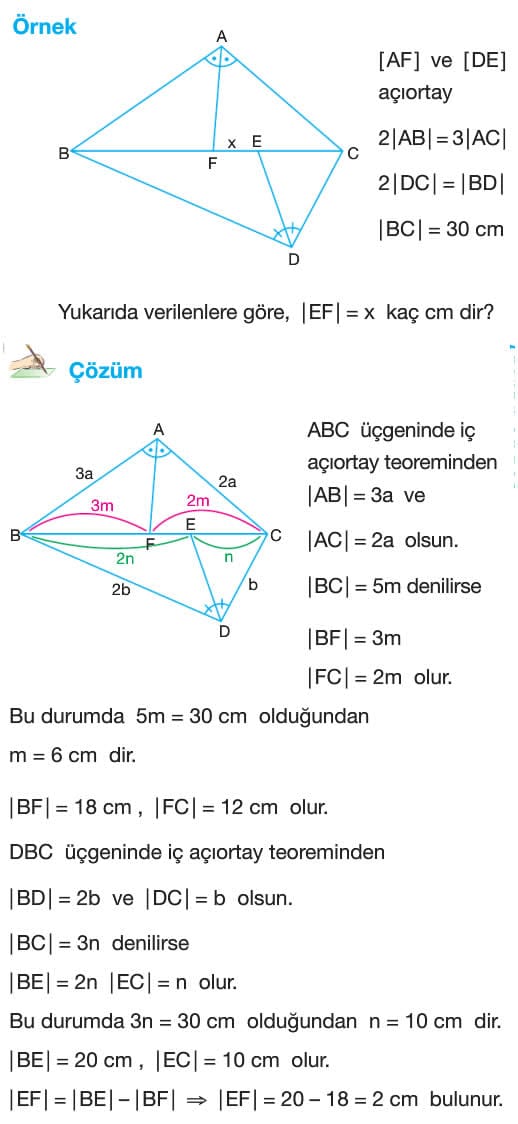
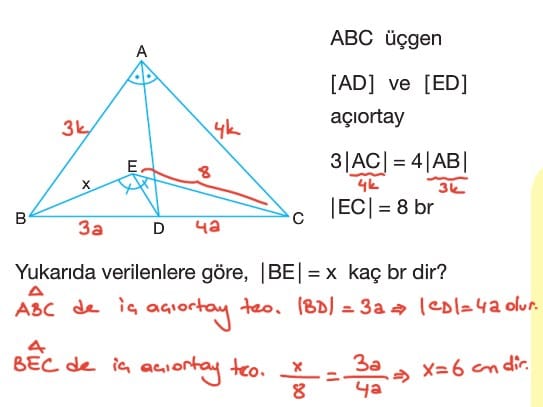
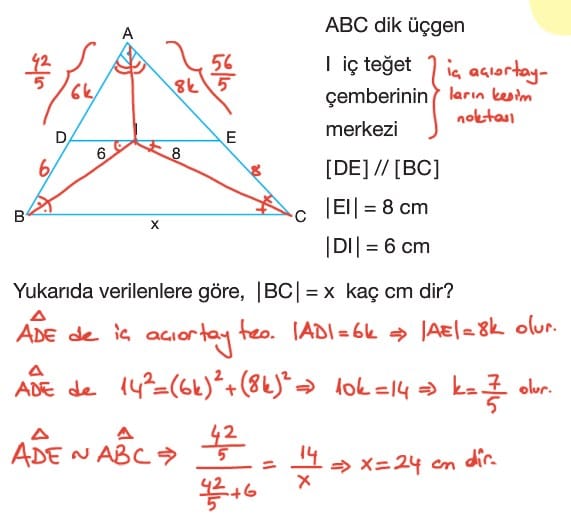
Soru: BC tabanları ortak olan ABC ve DBC üçgenleri veriliyor. F ve E noktaları BC tabanı üzerinde olmak üzere AF ve DE açıoartaylardır.
2|AB| = 3|AC|
2|AB| = 3|AC|
|BC| = 30 cm olmak üzere EF uzunluğu kaç cm dir?
Çözüm: ABC üçgeninde iç açıortay teoreminden
|AB| = 3a ve |AC| = 2a olsun.
|BC| = 5m denilirse |BF| = 3m, |FC| = 2m olur.
Bu durumda 5m = 30 cm olduğundan m 6 cm bulunur. Buradan |BF| = 18 cm, |FC| = 12 cm olur.
DBC üçgeninde iç açıortay teoreminden |BD| = 2b ve |DC| = b olsun.
|BC| = 3n denilirse |BE| = 2n ve |EC| = n olur. Bu durumda 3n = 30 cm olacağından n = 10 cm dir.
|BE| = 20 cm, |EC| = 10 cm olur. |EF| = |BE| – |BF| ise |EF| = 20 – 18 = 2 cm bulunur.
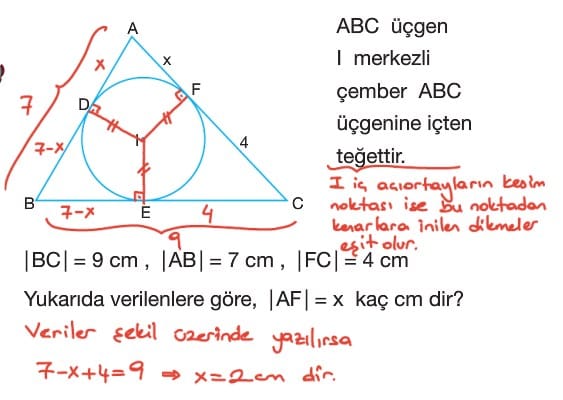
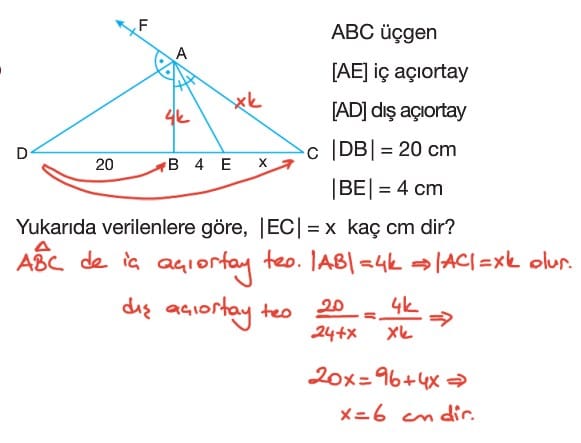
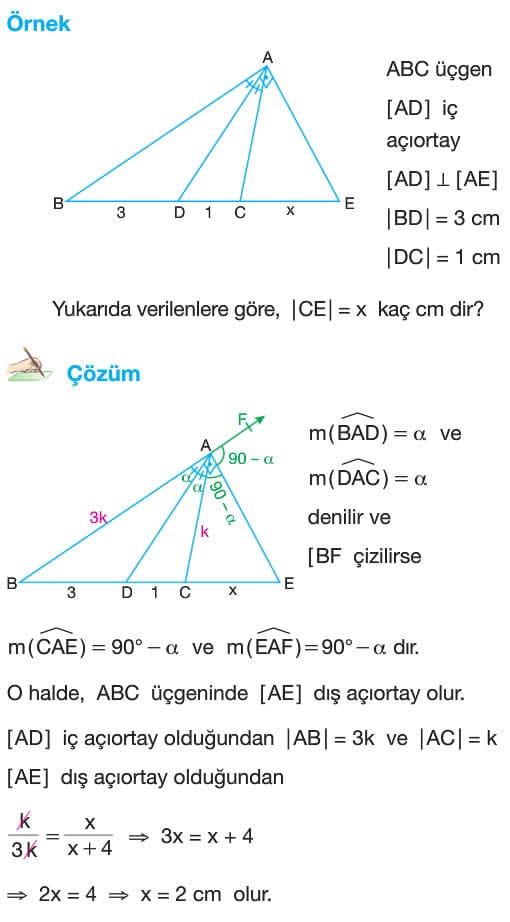
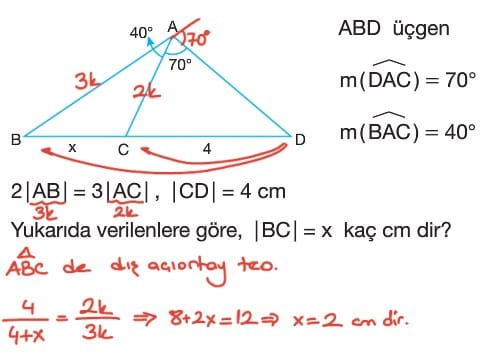
Soru: ABC üçgen, AD iç açıortay, AD ve AE dik, |BD| = 3 cm, |DC| = 1 cm olduğuna göre CE uzunluğu kaç cm dir?
Çözüm: BAD açısının ölçüsü alfa ve DAC açısının ölçüsü alfa denilir ve BF ışını çizilirse CAE açısının ölçüsü 90 – alfa ve EAF açısının ölçüsü 90 – alfa dır. O halde, ABC üçgeninde AE doğru parçası dış açıortay olur. AD doğru parçası iç açıortay olduğundan AB uzunluğu 3k ve AC uzunluğu k olur. AE doğru parçası dış açıortay olduğundan k / 3k = x / x + 4 ise 3x = x + 4 ise x = 2 cm olur.
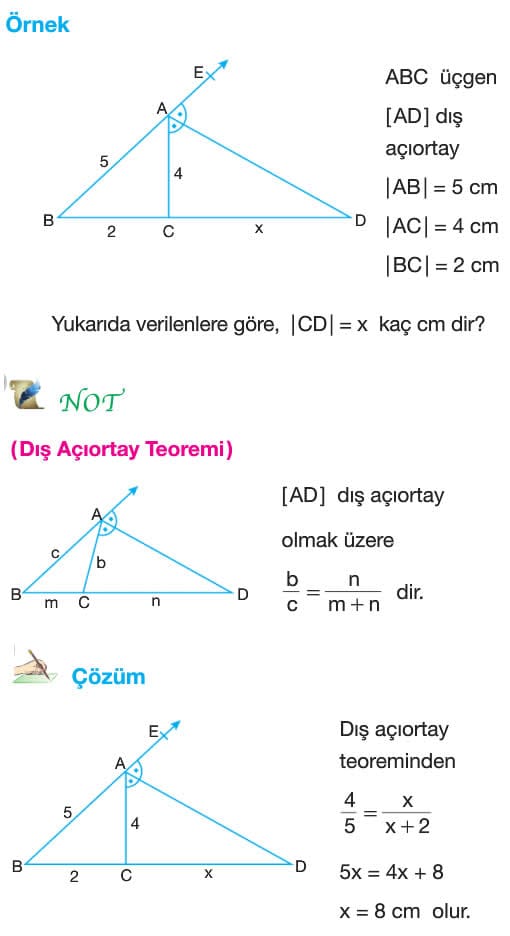
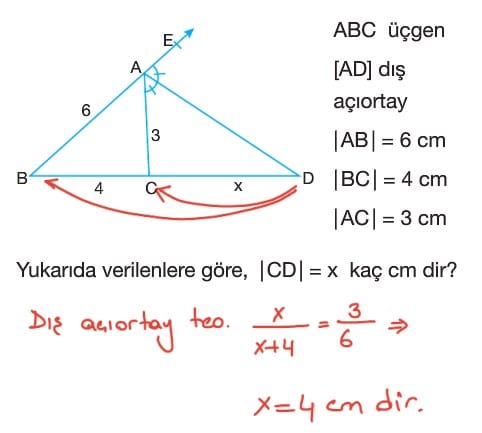
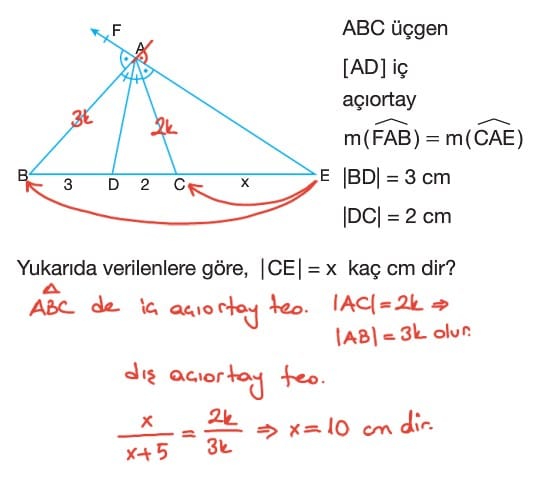
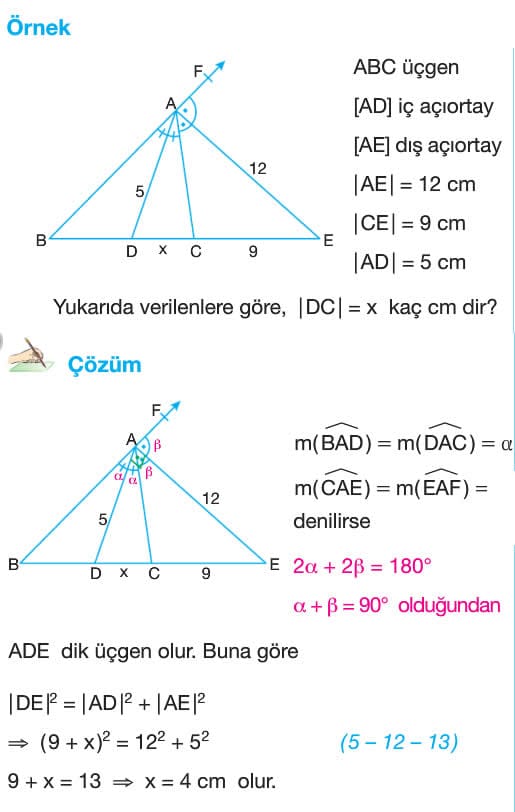
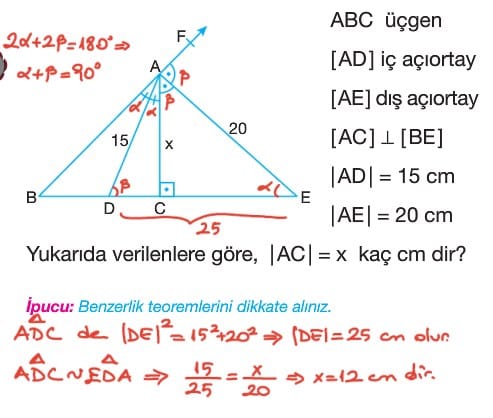
Soru: ABC üçgeninde AD doğru parçası iç açıortay ve AE doğru parçası dış açıortay olmak üzere, AE = 12 cm, CE = 9 cm ve AD = 5 cm veriliyor. Verilen bilgilere göre DC uzunluğu kaç cm dir?
Çözüm: BAD açısısının ölçüsü ile DAC açısının ölçüsü birbirine eşit olduğundan bunlara alfa diyelim. CAE ve EAF açılarının ölçülerine de beta diyelim. Buradan 2alfa + 2beta = 180 derece olduğundan alfa + beta 90 derece bulunur. ADE dik üçgen olur. Buna göre pisagor teoreminden DE uzunluğunun karesi = AD uzunluğunun karesi + AE uzunluğunun karesi ise bu denklem çözüldüğünde x = 4 cm olur.