Üçgende Açılar 9. Sınıf Matematik Ders Notu (Yeni Müfredat)
Üçgenler, geometrinin en temel şekillerindendir ve açıların özelliklerini anlamak, üçgenleri daha iyi kavramanın anahtarıdır. Üçgenin iç açılarının toplamının her zaman 180 derece olması, üçgenin açılarıyla ilgili temel bir kuraldır. Ayrıca, bir üçgenin herhangi bir dış açısının, komşu olmayan iki iç açının toplamına eşit olması gibi kurallar, üçgen problemlerini çözmekte kullanılır. Günlük hayatta üçgenler mimariden doğaya kadar birçok yerde karşımıza çıkar ve bu durum üçgenlerin açılarının hesaplanmasını daha anlamlı hale getirir. Yeni nesil matematik soruları, üçgenlerin açılar konusunu gerçek yaşam problemleriyle ilişkilendirerek öğrencilerin düşünme ve yorumlama becerilerini geliştirmeyi hedefler.
9. Sınıf Üçgende Açılar Testleri
9. Sınıf Üçgende Açılar Testleri (Yeni Müfredat)
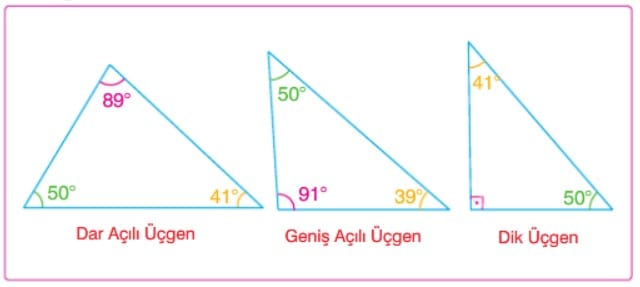
Açı Çeşitleri
Ölçülerine Göre Açı Çeşitleri

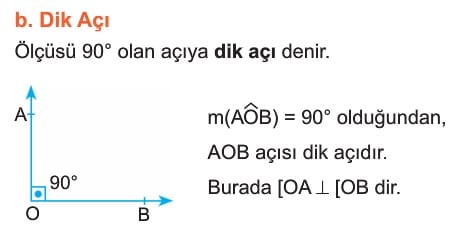
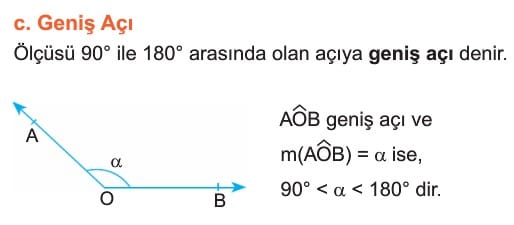
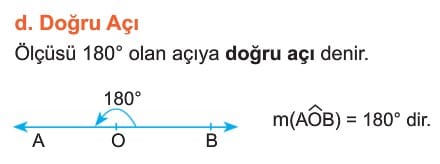
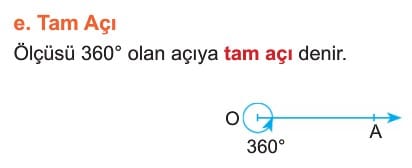
Diğer Açı Çeşitleri
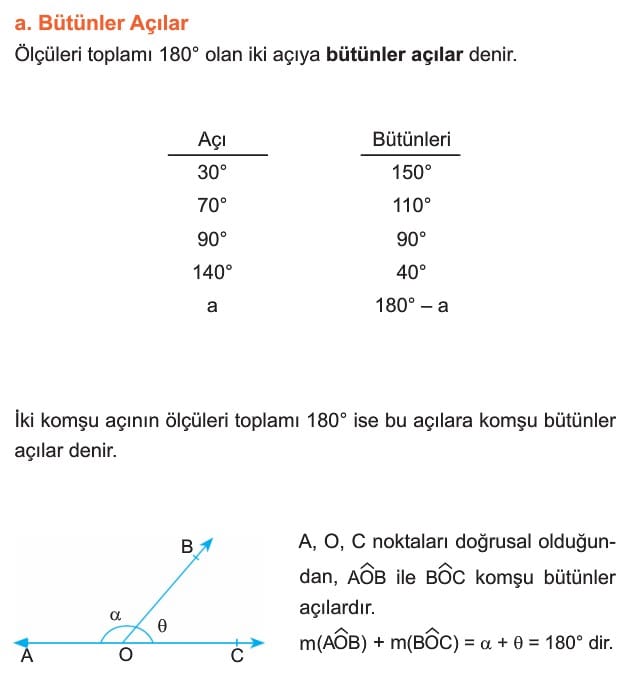
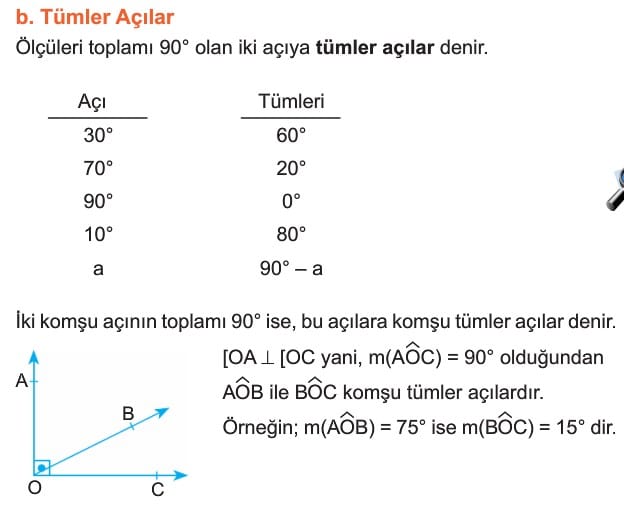
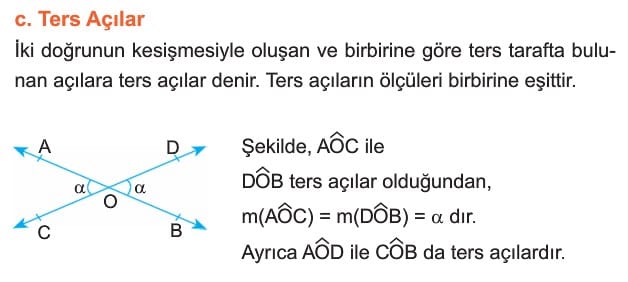
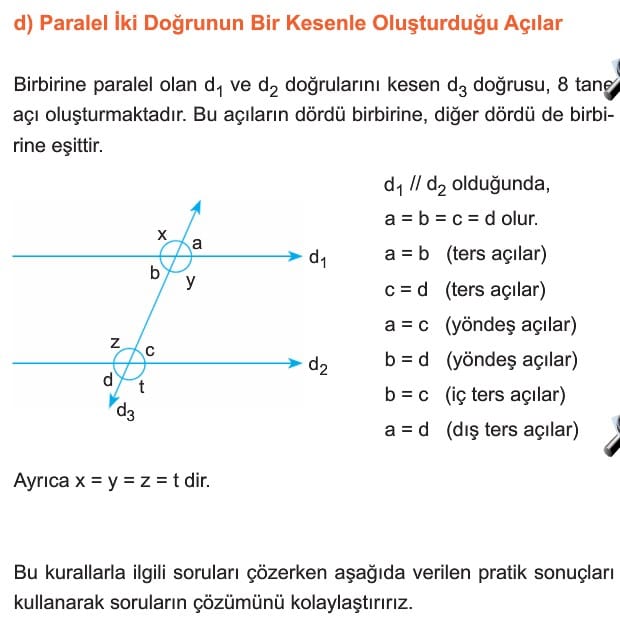
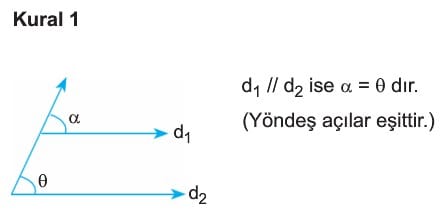
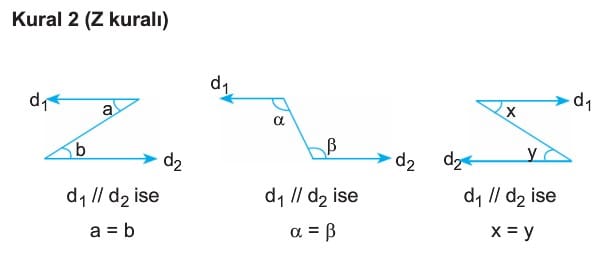
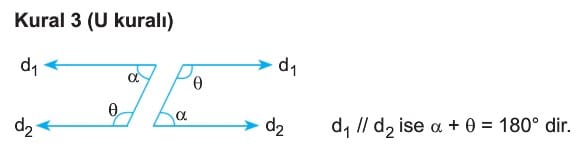
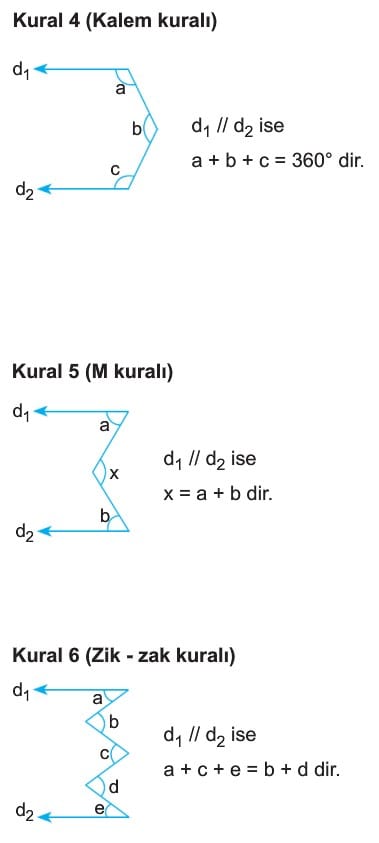
Çözümlü Sorular
Üçgende Açılar
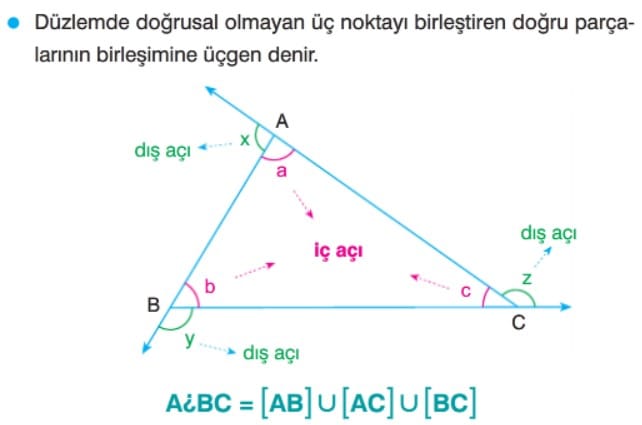
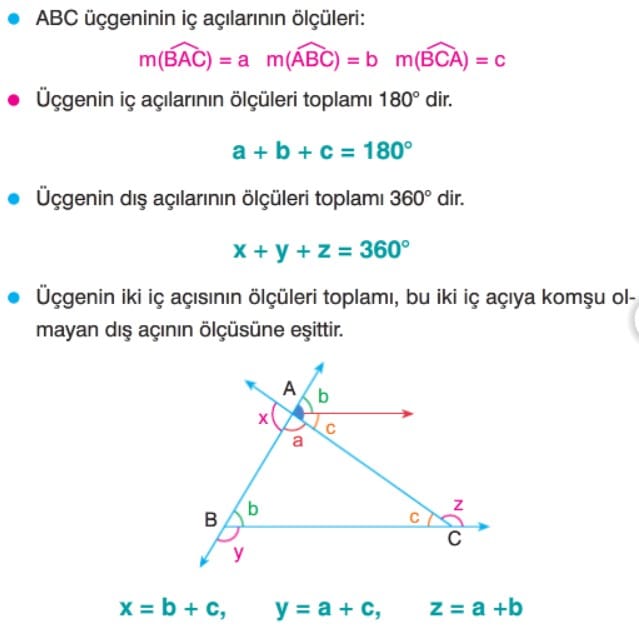
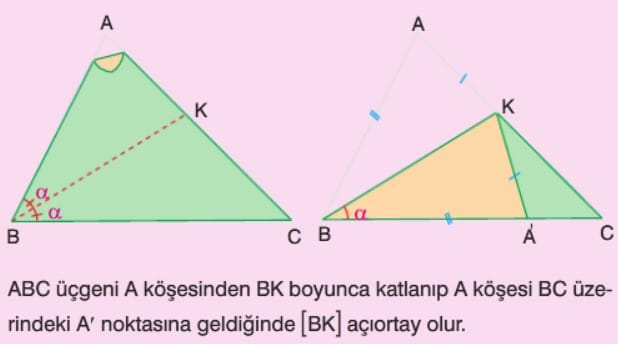
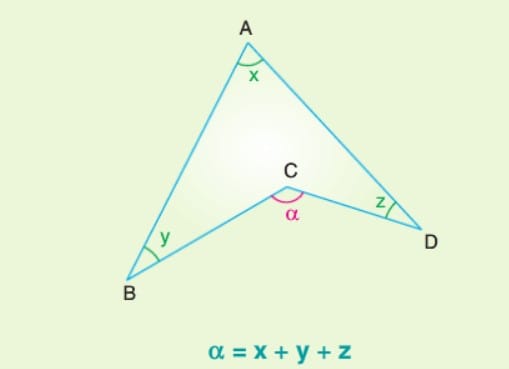
Çözümlü Sorular
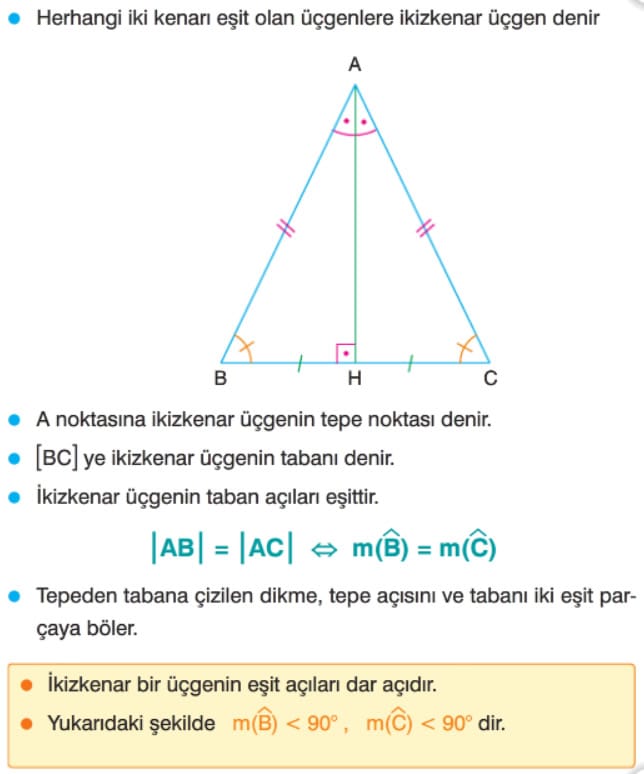
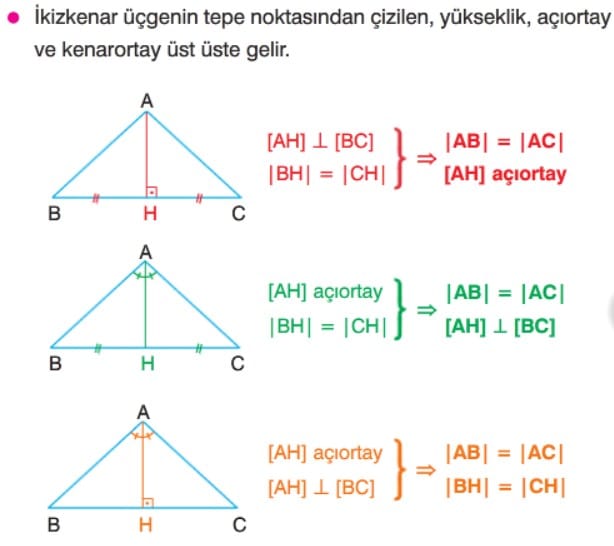
İkizkenar Üçgende Açılar
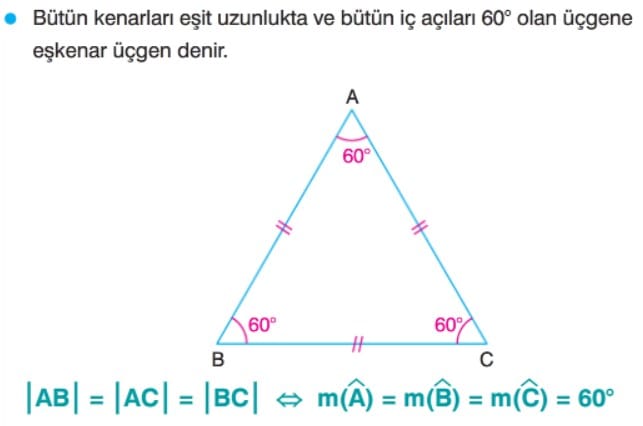
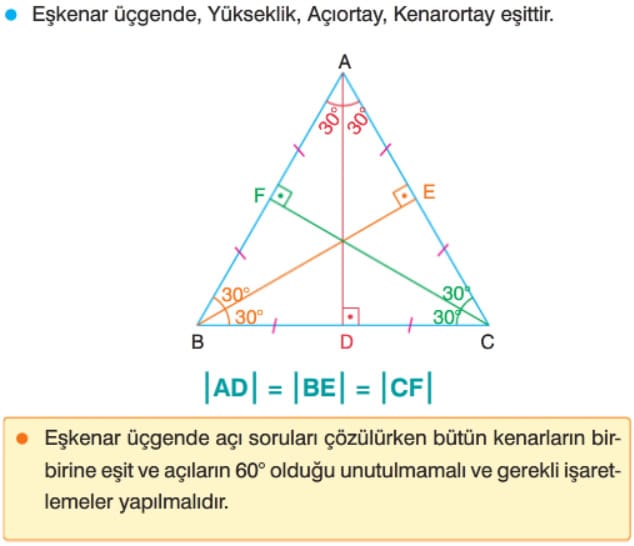
Eşkenar Üçgende Açılar
Çözümlü Sorular
Üçgende Açılar 1 Rehber Matematik
Üçgende Açılar 2 Rehber Matematik
Üçgende Açılar 3 Rehber Matematik
Üçgende Açılar 4 Rehber Matematik
Üçgende Açılar 5 Rehber Matematik
Üçgende Açılar 6 Rehber Matematik
Üçgende Açılar 7 Rehber Matematik
Üçgende Açılar 8 Rehber Matematik
Çözümlü Örnek Test Soruları
Soru 1
Bir üçgende iç açılar toplamı kaç derecedir?
A) 90°
B) 120°
C) 180°
D) 240°
E) 360°
Çözüm:
Bir üçgenin iç açılarının toplamı her zaman 180°’dir.
Cevap: C
Soru 2
Bir üçgende iki iç açının ölçüsü 50° ve 60° ise, üçüncü açının ölçüsü kaç derecedir?
A) 50°
B) 60°
C) 70°
D) 80°
E) 90°
Çözüm:
İç açılar toplamı 180° olduğundan, üçüncü açı = 180° – (50° + 60°) = 70° bulunur.
Cevap: C
Soru 3
Bir dik üçgende dik açının ölçüsü kaç derecedir?
A) 30°
B) 45°
C) 60°
D) 90°
E) 120°
Çözüm:
Dik üçgende bir açı her zaman 90° olur.
Cevap: D
Soru 4
Bir üçgende iki açının toplamı üçüncü açıya eşitse, bu üçgenin özel adı nedir?
A) Eşkenar üçgen
B) Dik üçgen
C) İkizkenar üçgen
D) Dar açılı üçgen
E) İkizkenar dik üçgen
Çözüm:
İki açının toplamı üçüncü açıya eşitse, bu üçgen dik üçgendir.
Cevap: B
Soru 5
Bir üçgenin iç açılarından biri 40°, diğeri 50° ise bu üçgenin üçüncü açısı aşağıdakilerden hangisidir?
A) 60°
B) 70°
C) 80°
D) 90°
E) 100°
Çözüm:
İç açılar toplamı 180° olduğundan, üçüncü açı = 180° – (40° + 50°) = 90° bulunur.
Cevap: D
Soru 6
Bir üçgenin dış açılar toplamı kaç derecedir?
A) 90°
B) 120°
C) 180°
D) 240°
E) 360°
Çözüm:
Bir üçgenin dış açılarının toplamı her zaman 360°’dir.
Cevap: E
Soru 7
Bir üçgende bir iç açının ölçüsü 80° ise, bu açının dış açısının ölçüsü kaç derecedir?
A) 80°
B) 90°
C) 100°
D) 120°
E) 180°
Çözüm:
Bir iç açı ile dış açısı toplamı 180° olduğundan, dış açı = 180° – 80° = 100° olur.
Cevap: C
Soru 8
Bir üçgende bir iç açı 70°, diğer iç açı 50° ve bu iki açının toplamı üçüncü açıdan küçükse, üçüncü açının türü aşağıdakilerden hangisidir?
A) Dar açı
B) Dik açı
C) Geniş açı
D) Tam açı
E) Keskin açı
Çözüm:
Üçüncü açının ölçüsü = 180° – (70° + 50°) = 60°’dir, bu da dar açıdır.
Cevap: A
9. Soru
Ayşe, bir doğa yürüyüşü sırasında üçgen şeklinde bir yol ayrımına rastlar. Yolların birleştiği köşedeki açı 50 derece, diğer iki yol arasındaki açılar ise eşittir. Ayşe, üç yol arasındaki eşit açıyı öğrenmek istiyor. Bu açı kaç derecedir?
a) 60
b) 65
c) 70
d) 75
e) 80
Çözüm:
Üçgenin iç açıları toplamı 180 derece olduğundan:
50 + 2x = 180
2x = 130
x = 65
Cevap: b) 65
10. Soru
Bir mühendis, bir köprünün üçgen şeklindeki destek yapısının açılarını tasarlıyor. Desteklerin bir açısı 40 derece, diğer açısı ise 50 derece olarak ölçülmüştür. Üçüncü açı kaç derecedir?
a) 70
b) 80
c) 90
d) 100
e) 110
Çözüm:
Üçgenin iç açıları toplamı 180 derece olduğundan:
40 + 50 + x = 180
x = 180 – 90
x = 90
Cevap: c) 90
11. Soru
Ali, üçgen biçimindeki bir oyun alanında oyun oynarken köşelerden birinin 120 derece olduğunu fark eder. Bu köşenin komşu olmayan iç açıları 40 derece ve x derece olarak ölçülmüştür. x açısı kaç derecedir?
a) 60
b) 70
c) 80
d) 90
e) 100
Çözüm:
Dış açılar teoremine göre:
120 = 40 + x
x = 120 – 40
x = 80
Cevap: c) 80
12. Soru
Bir dik üçgende, dik kenarların uzunlukları 5 cm ve 12 cm olarak ölçülmüştür. Hipotenüsün uzunluğu kaç cm’dir?
a) 13
b) 14
c) 15
d) 16
e) 17
Çözüm:
Pisagor teoremi uygulanır:
c² = 5² + 12²
c² = 25 + 144
c² = 169
c = 13
Cevap: a) 13
13. Soru
Bir inşaat projesinde üçgen şeklinde bir yapı tasarlanmıştır. Bu yapıda bir dış açı 130 derece olarak ölçülmüştür. Bu dış açının komşu olmayan iki iç açısından biri 50 derece olduğuna göre, diğer iç açı kaç derecedir?
a) 60
b) 70
c) 80
d) 90
e) 100
Çözüm:
Dış açılar toplamı, komşu olmayan iç açılara eşittir:
130 = 50 + x
x = 130 – 50
x = 80
Cevap: c) 80








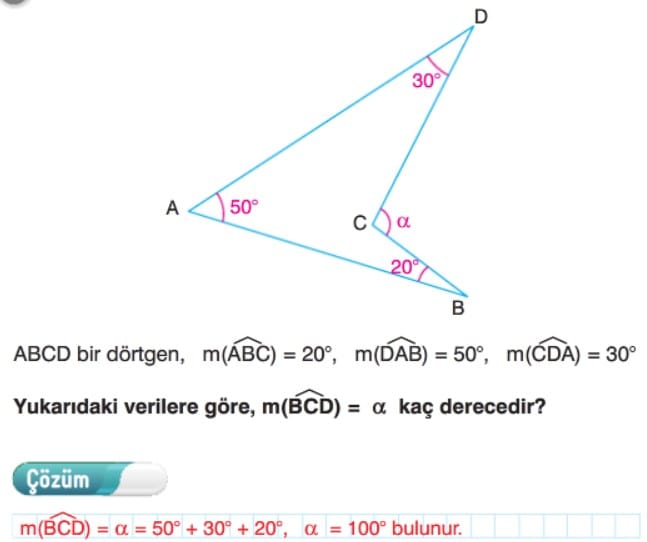
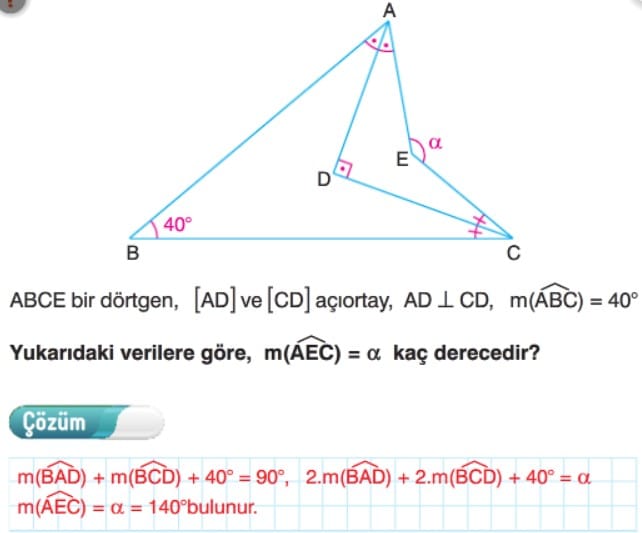
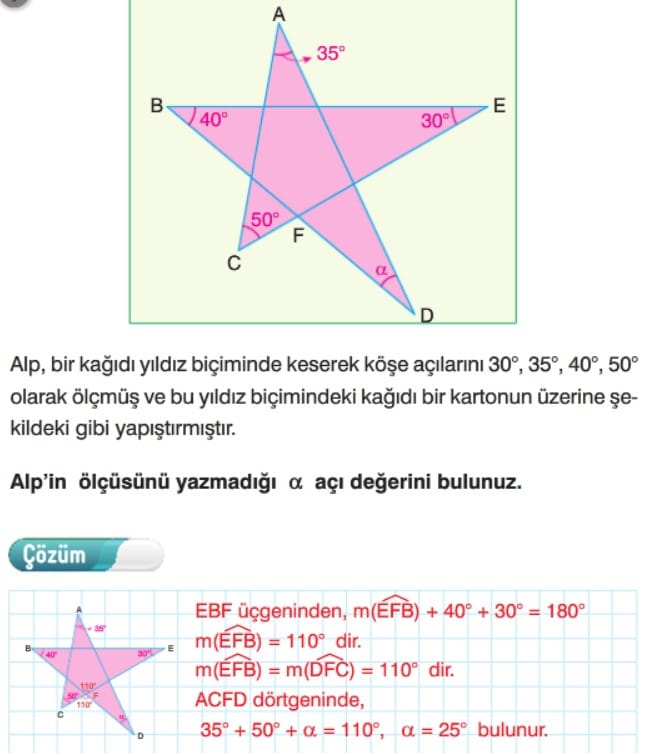

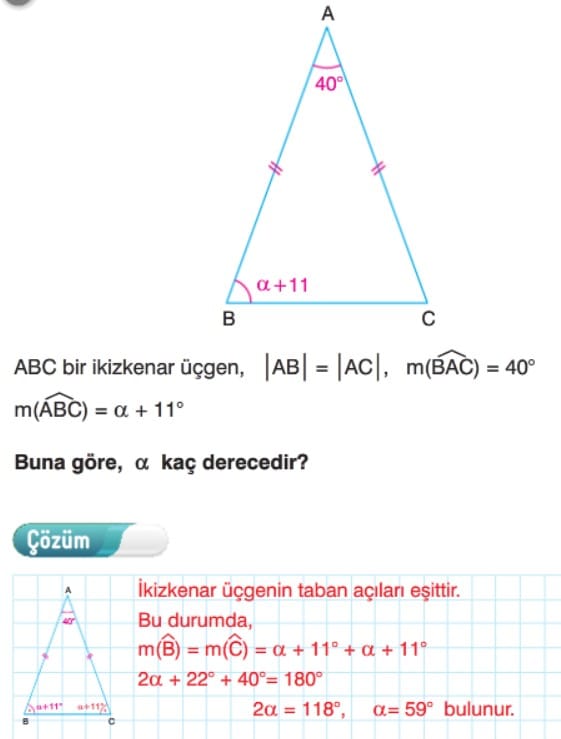


İl Perfecto