Geometri, şekillerin ve düzlemdeki yapıların incelendiği önemli bir matematik dalıdır. Geometrik şekillerden biri olan üçgenler, üç kenarlı ve üç köşeli kapalı şekillerdir. Bu konuyu anlamak, öğrencilerin temel geometri bilgisini geliştirmek ve farklı türdeki şekilleri tanımalarına yardımcı olacaktır. 5. sınıf öğrencileri için üçgenlerin tanımı, çeşitleri ve özellikleri üzerinde durulacak, açılarına ve kenarlarına göre üçgenler ele alınacaktır.

5. Sınıf Üçgen ve Özellikleri Testleri

---

5. Sınıf Üçgen ve Özellikleri Ders Notu (Yeni Müfredat)

Açılarına ve Kenarlarına Göre Üçgenler

Üç doğrunun ardışık olarak ve ilk doğru ile son doğrunun da kesiştiği durumda oluşan geometrik şekle üçgen denir.

Örnek:

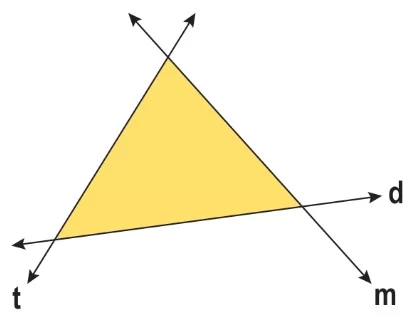
Üçgenler açılarına ve kenarlarına göre sınıflandırılırlar.

Aşağıdaki üçgen şeklindeki kâğıt, makas yardımıyla kesilerek elde edilen parçalar, d doğrusu üzerindeki O noktasında A, B ve C köşeleri çakıştırılarak yerleştirilmiştir.

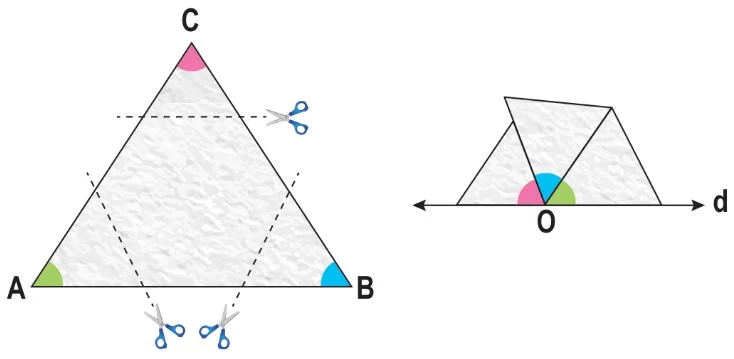
Üçgenin iç açılarının ölçüleri toplamı 180⁰ dir.

Açılarına Göre Üçgenler

Dik Açılı Üçgen: Herhangi bir açısının ölçüsü 90° olan üçgendir. Dik açılı üçgende diğer iki açı dar açıdır.

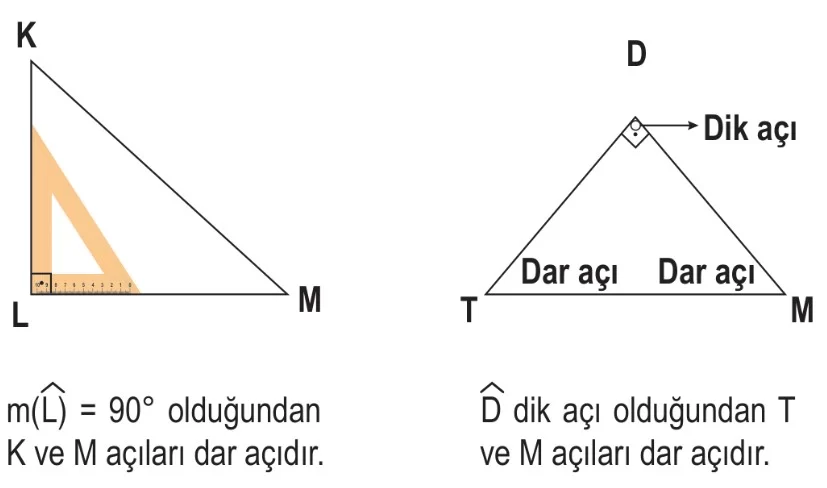
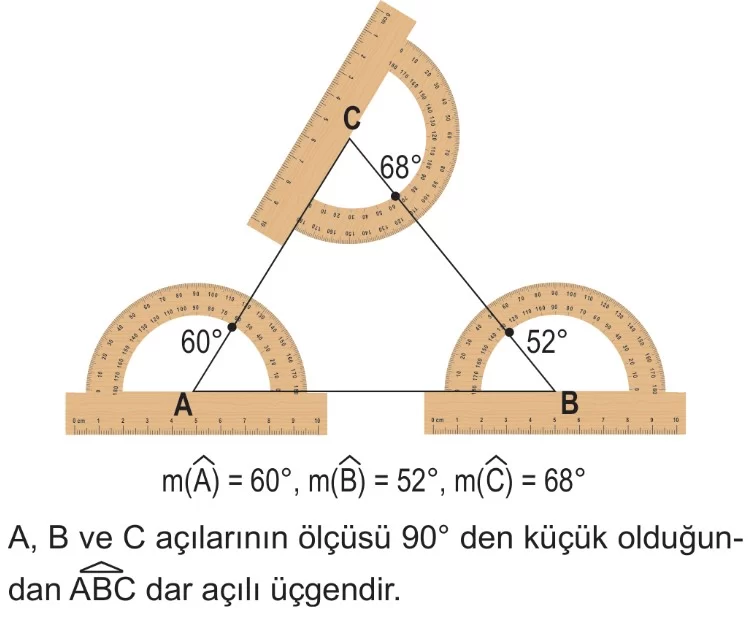
Dar Açılı Üçgen: Bütün açıları dar açı olan üçgenlerdir (yani her açı 90°’den küçüktür).

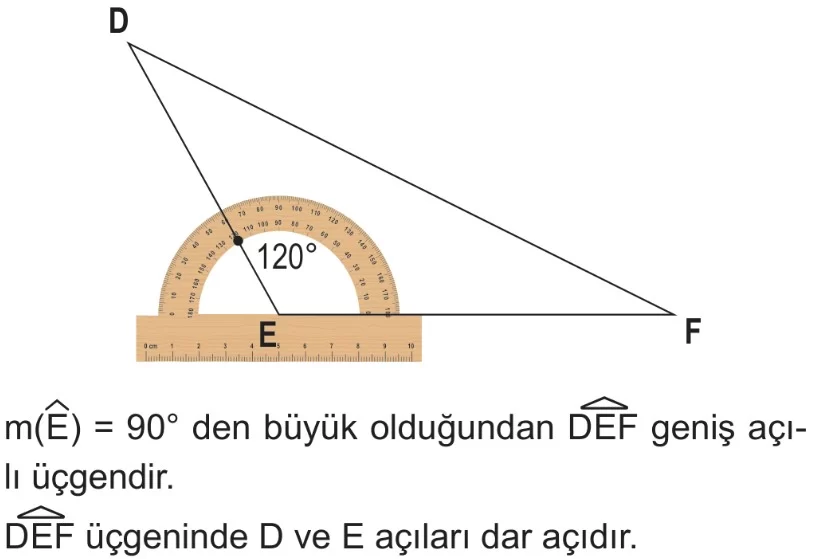
Geniş Açılı Üçgen: Bir iç açısı geniş açı olan üçgenlerdir (yani bir açı 90°’den büyüktür).

Kenarlarına Göre Üçgenler

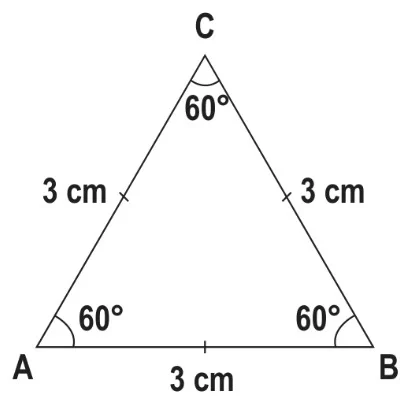
Eşkenar Üçgen: Üç kenar uzunluğu birbirine eşit olan üçgenlerdir. İç açıları eşit olup, her biri 60°’dir. Eşkenar üçgenlerde dik ya da geniş açı bulunmaz.

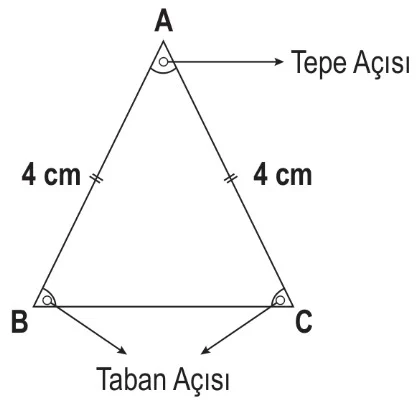
İkizkenar Üçgen: İki kenar uzunluğu eşit olan üçgenlerdir. Eşit uzunluktaki kenarları gören iç açıların ölçüleri de eşittir. Taban açıları birbirine eşittir ve tepe açısı dar, dik ya da geniş açı olabilir.

Çeşitkenar Üçgen: Üç kenar uzunluğu birbirinden farklı olan üçgenlerdir. İç açıları dar, dik veya geniş açı olabilir.

---

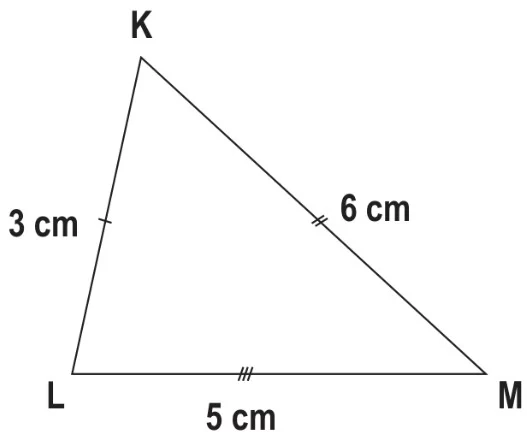
Çözümlü Sorular

Soru 1:

Bora ve arkadaşları sınıfta bir yarışma düzenlediler. Bora’nın görevi, üç farklı uzunlukta çubuk kullanarak bir üçgen oluşturmak. Çubukların uzunlukları 6 cm, 8 cm ve 10 cm’dir. Bora, bu üçgenin bir dik üçgen olduğunu düşünerek kazandığını ilan etti. Bora’nın düşüncesi doğru mu?
A) Evet
B) Hayır

Çözüm:
Bir üçgenin dik üçgen olup olmadığını anlamak için Pisagor Teoremi kullanılır:

• a² + b² = c² olmalıdır (burada c, en uzun kenardır).
• Hesaplayalım:
  6² + 8² = 10²
  36 + 64 = 100
  100 = 100
  Bu nedenle, Bora haklıdır. Bu üçgen bir dik üçgendir.
  Doğru Cevap: A

Soru 2:

Zeynep, bir akşam masa üstünde üçgen oluşturmayı deniyordu. 7 cm, 7 cm ve 7 cm uzunluğunda çubuklar kullandı. Sonrasında babası ona şu soruyu sordu: “Zeynep, bu üçgenin iç açılarından biri kaç derecedir?” Zeynep’in doğru cevabı ne olmalıdır?
A) 30°
B) 45°
C) 60°
D) 90°

Çözüm:
Tüm kenarları eşit olan bir üçgen, eşkenar üçgendir. Bir eşkenar üçgenin tüm açıları eşit ve her biri 60°’dir.
Doğru Cevap: C

Soru 3:

Ahmet, köyünde bir arazi ölçüm işine yardım ediyordu. Arazinin köşeleri arasında bir üçgen şekli oluşmuştu. Üçgenin açıları sırasıyla 120°, 30° ve 30° olarak ölçüldü. Ahmet, bu üçgenin türünü merak etti. Bu üçgenin türü nedir?
A) Dik Açılı Üçgen
B) Geniş Açılı Üçgen
C) Dar Açılı Üçgen
D) Eşkenar Üçgen

Çözüm:
Bir üçgenin bir açısı 90°’den büyükse bu üçgen geniş açılı üçgendir. Bu üçgende 120° olduğundan geniş açılıdır.
Doğru Cevap: B

Soru 4:

Ali’nin matematik öğretmeni ona bir görev verdi. Görevde üçgenin kenar uzunlukları 9 cm, 12 cm ve 15 cm’di. Öğretmen, Ali’den bu üçgenin bir dik üçgen olup olmadığını kontrol etmesini istedi. Ali, hangi yöntemi kullanarak bu soruyu çözebilir?
A) Üçgenin iç açılarını ölçerek
B) Pisagor Teoremi ile
C) Kenar uzunluklarını toplayarak
D) Üçgenin çevresini hesaplayarak

Çözüm:
Bir üçgenin dik üçgen olup olmadığını anlamanın en iyi yolu, Pisagor Teoremini kullanmaktır:
9² + 12² = 15²
81 + 144 = 225
225 = 225
Bu nedenle, bu bir dik üçgendir. Ali doğru bir şekilde Pisagor Teoremi’ni kullanabilir.
Doğru Cevap: B

Soru 5:

Ayşe, kardeşiyle birlikte üçgenlerle ilgili bir oyun oynuyordu. Oyunda, Ayşe 12 cm, 12 cm ve 20 cm uzunluğunda kenarlara sahip bir üçgen oluşturdu. Kardeşi ona şu soruyu sordu: “Bu üçgenin türü nedir?”
A) Eşkenar Üçgen
B) İkizkenar Üçgen
C) Çeşitkenar Üçgen
D) Dik Üçgen

Çözüm:
Bir üçgende iki kenar eşit uzunlukta ise bu üçgen ikizkenar üçgen olarak adlandırılır. Ayşe’nin üçgeninde 12 cm ve 12 cm eşit olduğundan, bu bir ikizkenar üçgendir.
Doğru Cevap: B