Üçgen, geometride temel şekillerden biridir ve en az üç doğru parçasının kesişmesiyle oluşur. Özellikle çemberlerle yapılan üçgen inşası, hem eğlenceli hem de öğretici bir çalışma olarak geometri derslerinde sıklıkla kullanılır. İki çemberin kesişim noktaları ile oluşturulan üçgenler, öğrencilerin geometri anlayışını geliştirmelerine yardımcı olur. Bu yöntem, geometrik şekilleri oluşturmak ve anlamak için önemli bir teknik sağlar. Bu konuda, yarıçapları eş veya farklı olan çemberlerin kesişiminden nasıl üçgenler oluşturulacağını inceleyeceğiz.

5. Sınıf Üçgen İnşası Testleri

5. Sınıf Üçgen İnşası Ders Notu (Yeni Müfredat)

Düzlemde iki çemberin kesişimiyle oluşan üçgenleri inceleyelim.

a. Yarıçapları eş iki çember kesişirse,

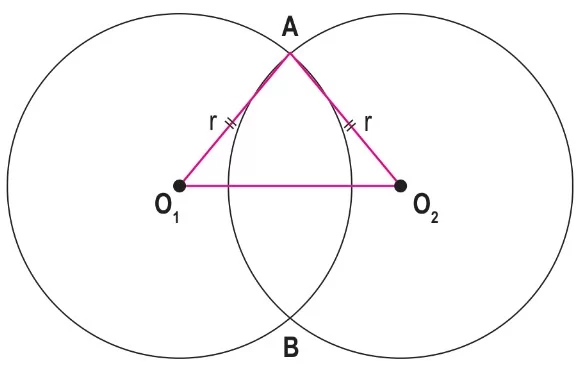
• Merkezleri O_₁ ve O_₂ olan yarıçapları eş iki çemberin kesişimine A ve B noktaları oluşur.
• Çemberlerin yarıçapları eşit olduğu için köşeleri A, O_₁ ve O_₂ olan üçgen, ikizkenar üçgendir.
• İkizkenar üçgenlerin eş kenarları |O_₁A| = |O_₂A|’dır ve bu kenarlar çemberin yarıçapıdır.

b. Yarıçapları eş iki çember birbirlerinin merkezinden geçecek şekilde kesişirse,

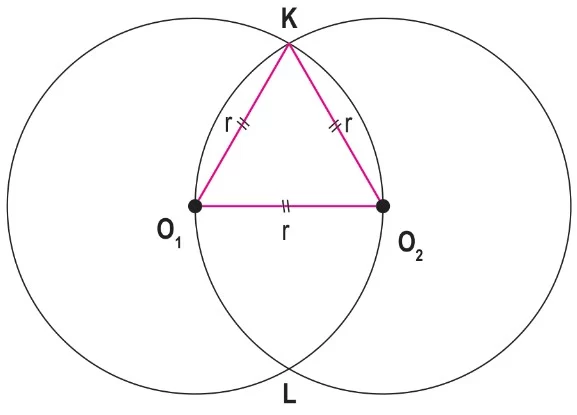
• O₁ merkezli çember O_₂’den,
• O_₂ merkezli çember O_₁’den geçecek şekilde kesişirse K ve L noktaları oluşur.
• Köşeleri K, O_₁ ve O_₂ olan üçgenin kenarları eş yarıçapları olduğundan eşkenar üçgendir.
• |O_₁K| = |O_₂K| = |O_₁O_₂| = r’dir.

c. Yarıçapları farklı iki çember kesişirse,

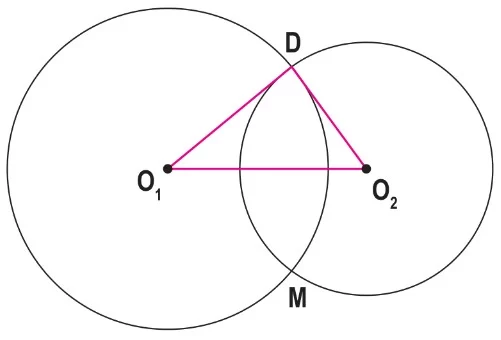
• Kesişimlerinde D ve M noktaları oluşur.
• Köşeleri D, O_₁ ve O_₂ olan üçgen çeşitkenar üçgendir.
• Üç kenar uzunluğu farklıdır.

d. Yarıçapları farklı büyüklükteki iki çemberden biri diğerinin merkezinden geçecek şekilde kesişirse,

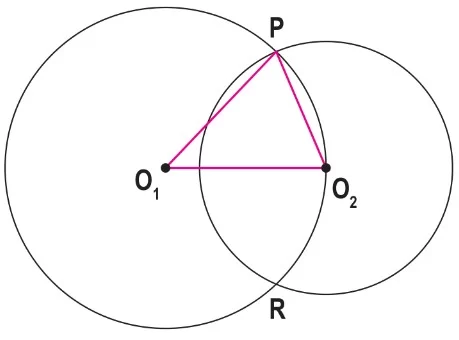
• O_₁ merkezli çember, O_₂ olan çemberin merkezinden geçecek şekilde kesişirse P ve R noktaları oluşur.
• Köşeleri O_₁ ve O_₂ olan üçgen iki kenarı O_₁ merkezli çemberin yarıçapı olduğu için ikizkenar üçgendir.

Aşağıda M.Ö. 300 yılları civarında yaşayan Öklid’in elemanlar kitabından bir örnek verilmiştir.

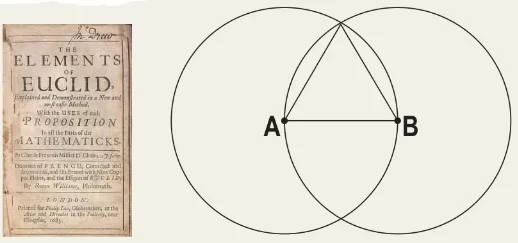
Bu kitapta çember çiftlerinin kesişimiyle oluşan eşkenar üçgen gibi pek çok çizim yer almaktadır.

• Çemberin kesişiminden oluşan pek çok örneği günlük yaşantımızda görebiliriz.
  Örneğin; İki çemberin kesişimiyle oluşan üçgenleri inceleyelim.

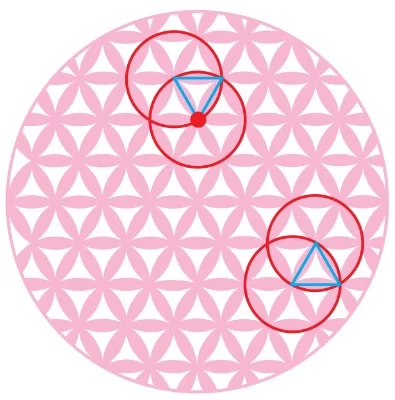
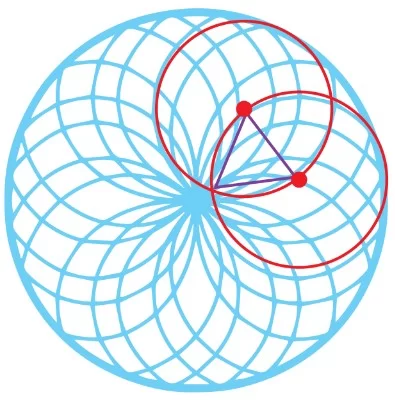
• Yarıçapları eş olan ve birbirinin merkezinden geçen çember çiftinin kesişim noktası ve merkezlerinin oluşturduğu üçgen de kenarlar yarıçap olduğundan eşkenar üçgen olur.

---

Çözümlü Örnek Test Soruları

Soru 1:

Ali ve Elif, üçgen inşası yapmak için birbirine eşit uzunlukta ipler kullanarak bir deney yapıyorlar. Ali, A noktasından başlayarak bir çember çiziyor. Elif ise B noktasından başlayarak bir çember çiziyor. Çemberler A ve B noktalarına eşit uzaklıkta bir noktada kesişiyor. Bu durumda, oluşacak üçgenin üçüncü köşesi olan kesişim noktası C ile A ve B noktaları arasındaki mesafe birbirine eşit.

Bu durumda aşağıdakilerden hangisi doğrudur?

A) Oluşacak üçgen, ikizkenar bir üçgendir.
B) Oluşacak üçgen, eşkenar bir üçgendir.
C) Oluşacak üçgen, dik üçgendir.
D) Üçgen oluşmaz, sadece bir doğru oluşur.

Çözüm: Ali ve Elif’in çizdiği çemberler, A ve B noktalarından eşit uzaklıktaki C noktasında kesişir. Bu durumda oluşacak üçgenin kenar uzunlukları eşit olur, yani üçgen bir eşkenar üçgendir.

Cevap: B) Oluşacak üçgen, eşkenar bir üçgendir.

Soru 2:

Bir öğretmen, tahtada A ve B noktalarını belirliyor ve öğrencilere bu noktaları kullanarak bir üçgen inşa etmelerini istiyor. Öğrenciler, A ve B noktalarından başlayan iki çember çiziyorlar. Çemberler iki farklı noktada kesişiyor: C ve D. Öğretmen, öğrencilerden A, B ve C noktalarını kullanarak bir üçgen oluşturmalarını istiyor.

Oluşan üçgenle ilgili aşağıdaki bilgilerden hangisi doğrudur?

A) Üçgenin çevresi, AB, BC ve CA uzunluklarının toplamına eşittir.
B) Üçgenin bir kenarı diğerlerinden uzun olur.
C) Üçgen oluşmaz çünkü üç nokta aynı doğru üzerinde değildir.
D) Üçgenin sadece iki kenarı eşit olur.

Çözüm: A ve B noktalarından çizilen çemberler C ve D noktalarında kesişir. Bu durumda, A, B ve C noktaları ile bir üçgen oluşur. Bu üçgenin çevresi, AB, BC ve CA uzunluklarının toplamına eşittir.

Cevap: A) Üçgenin çevresi, AB, BC ve CA uzunluklarının toplamına eşittir.

Soru 3:

Bir bahçede üçgen şeklinde bir çiçek alanı oluşturmak isteyen Elif, bahçenin köşelerine A ve B noktalarını işaretleyip, her iki noktadan birer çember çiziyor. Çemberler, A ve B noktalarına eşit uzaklıkta olan C noktasında kesişiyor. Elif, bu üç noktayı birleştirerek bir üçgen oluşturuyor.

Bu durumda Elif’in oluşturduğu üçgenle ilgili aşağıdakilerden hangisi doğrudur?

A) Oluşan üçgen bir ikizkenar üçgendir.
B) Üçgenin bütün kenar uzunlukları eşittir.
C) Üçgenin sadece bir açısı diktir.
D) Üçgen çizilmez, çünkü C noktası A ve B noktalarına uzak değildir.

Çözüm: Elif, A ve B noktalarından aynı uzaklıkta olan C noktasını bulduğuna göre, oluşturduğu üçgenin bütün kenar uzunlukları eşit olur. Bu nedenle üçgen bir eşkenar üçgendir.

Cevap: B) Üçgenin bütün kenar uzunlukları eşittir.