Üçgen Eşitsizliği 9. Sınıf
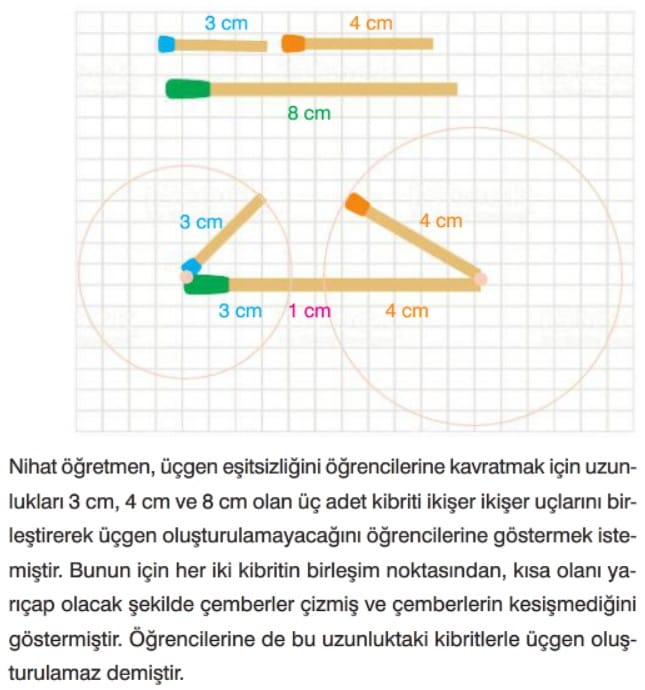
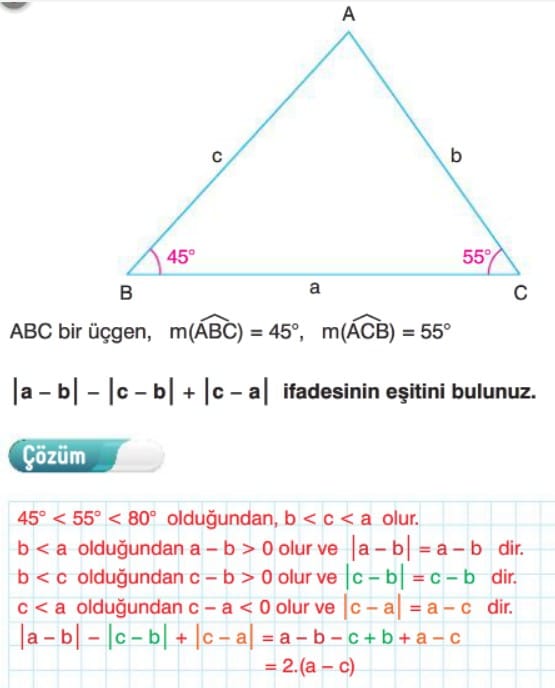
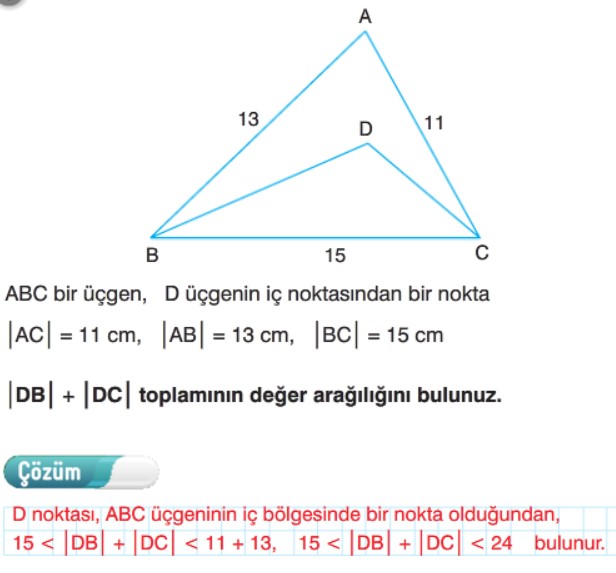
Örnek:

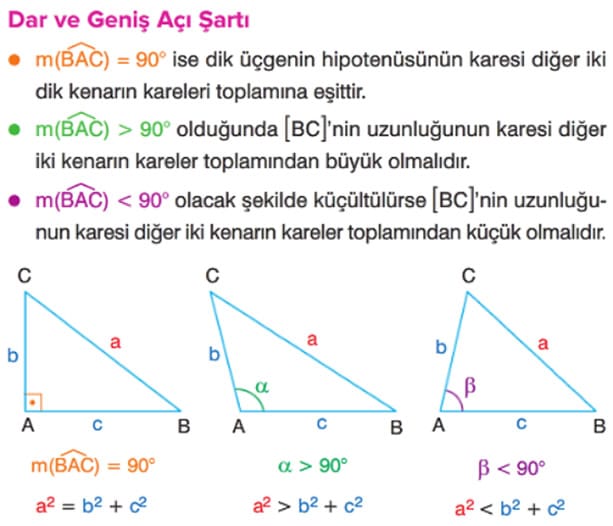
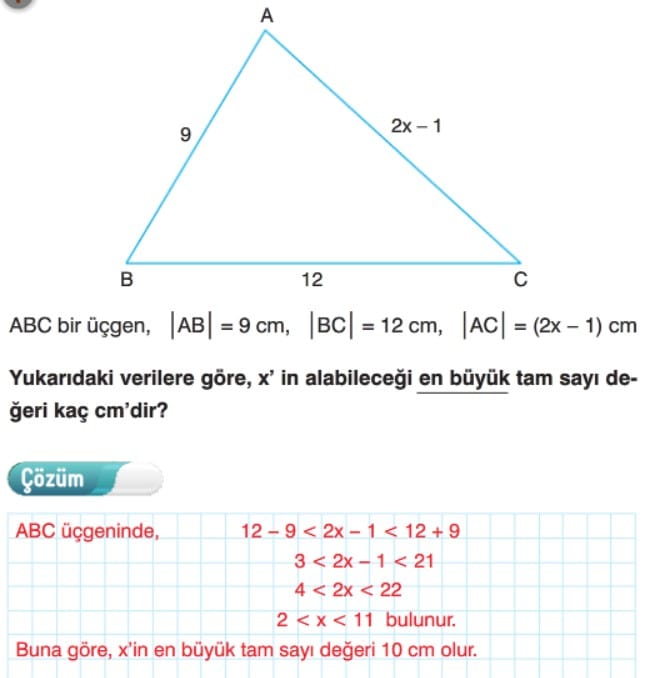
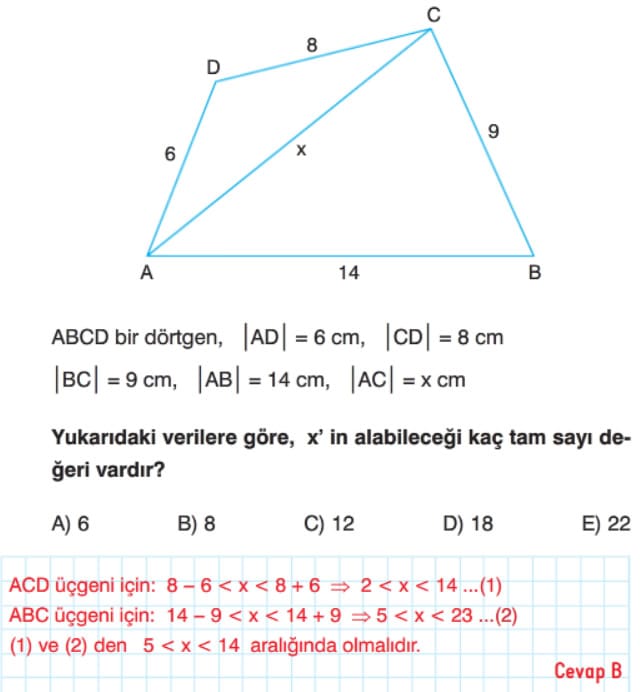
Örnek:

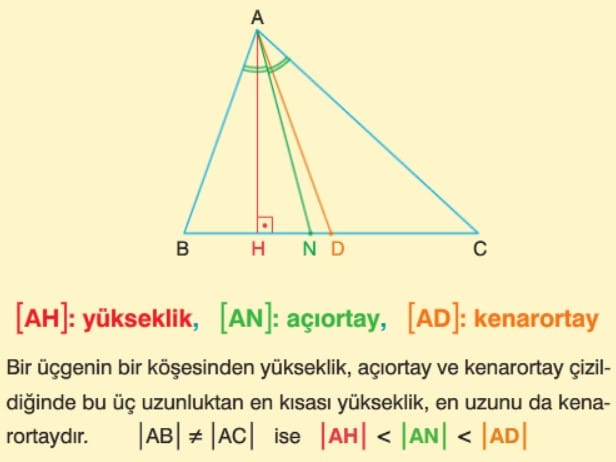
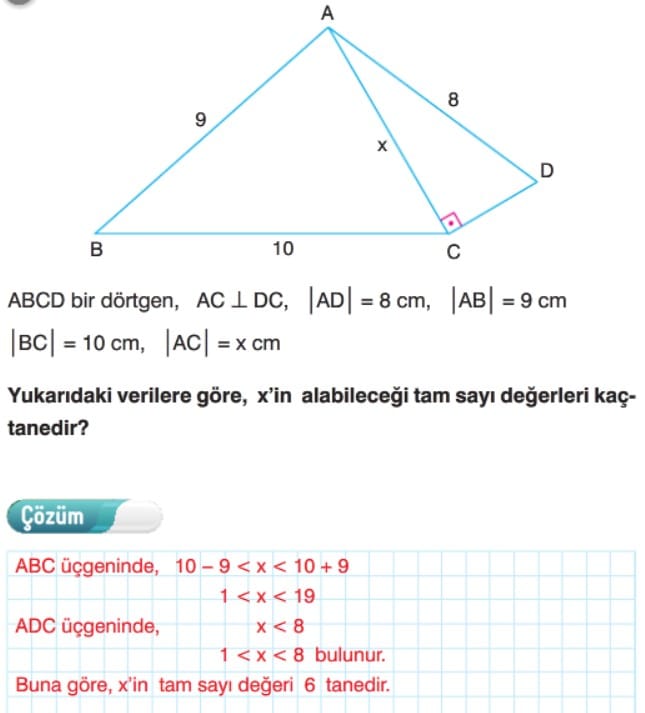
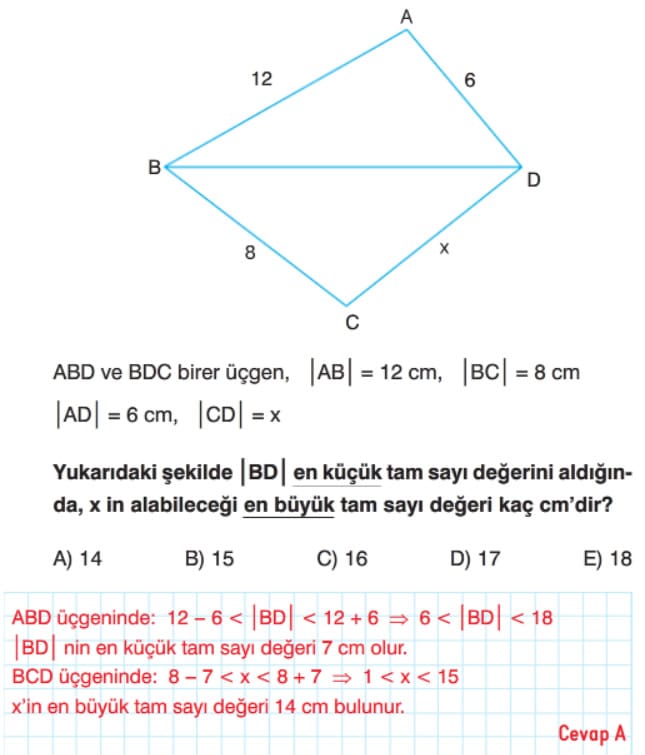
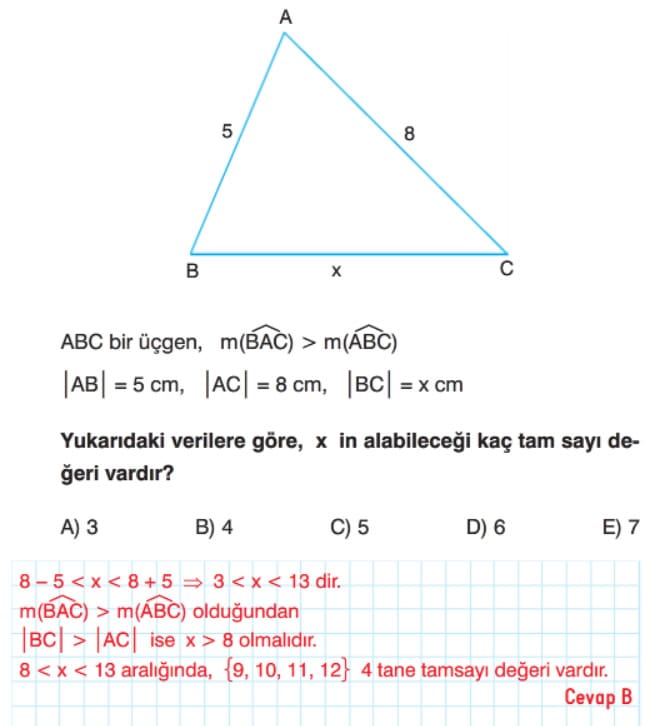
Örnek:

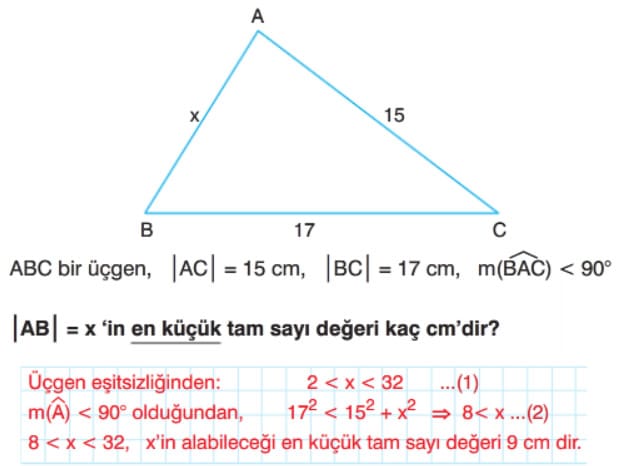
Üçgen Eşitsizliği Soruları ve Çözümleri
Üçgen Eşitsizliği konu anlatımı soruları çözümleri 9. Sınıf Matematik
Soru: Bir ABC üçgeninin kenar uzunlukları a, b, c olmak üzere, a.b = 24, c = 5 cm veriliyor. a ve b birer tam sayı olmak üzere, ABC üçgeninin çevresinin kaç cm olduğunu bulalım.
Çözüm: a ve b üçgenin kenar uzunlukları olduğundan, bunlar birer pozitif tam sayıdır. a . b = 24 ise 24 sayısının pozitif çarpanlarına bakalım. 24 = 24 . 1 ise a = 24, b = 1 cm ve c = 5 cm için 1 + 5 < 24 olur ve üçgen oluşmaz. 24 = 12 . 2 ise a = 12, b = 2 cm ve c = 5 cm için 2 + 5 < 12 olur ve üçgen oluşmaz. 24 = 8 . 3 ise a = 8, b = 3 cm ve c = 5 cm için 3 + 5 küçük eşit 8 olur ve üçgen oluşmaz. 24 = 6 . 4 ise a = 6, b = 4 cm ve c = 5 cm için 4 + 5 > 6 olur ve üçgen oluşur. Diğer çarpanlar a ve b için simetriktir. Çevre uzunluğunu değiştirecek farklı bir sonuç gelmez. Buna göre a = 6 cm, b = 4 cm ve c = 5 cm için Ç(ABC) = 15 cm dir.
Üçgen eşitsizliği, üç kenar uzunluğu verilen bir üçgenin olup olamayacağını belirleme amacı taşıyan bir kuraldır. 9. sınıf matematik müfredatında genellikle bu konu işlenir. Üçgen eşitsizliği kuralı, bir üçgenin kenar uzunlukları arasında belirli bir ilişki olduğunu belirtir.
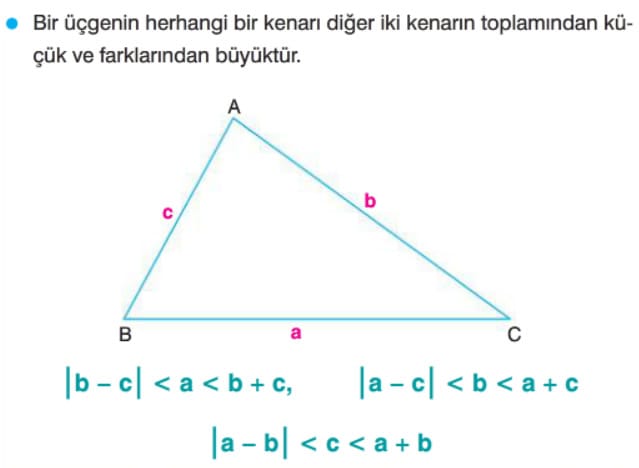
Üçgen Eşitsizliği Kuralı: Bir üçgenin kenar uzunlukları a, b ve c olsun. Üçgen eşitsizliği kuralı şu şekildedir:
a + b > c
a + c > b
b + c > a
Eğer bu eşitsizliklerden herhangi biri sağlanmazsa, o üçgen olamaz.
Üçgen Eşitsizliği Tarihçesi: Üçgen eşitsizliği kuralı, matematik tarihinde eski Yunan matematikçisi Thales tarafından öne sürülmüştür. Ancak, bu kuralın daha geniş bir şekilde ifade edilip kullanılması daha sonraki matematikçilere dayanmaktadır. Bu kural, geometri ve trigonometri gibi matematik dallarında önemli bir yer tutar ve birçok matematiksel problemin çözümünde temel bir prensip olarak kullanılır.