Türevin Uygulamaları 12. Sınıf
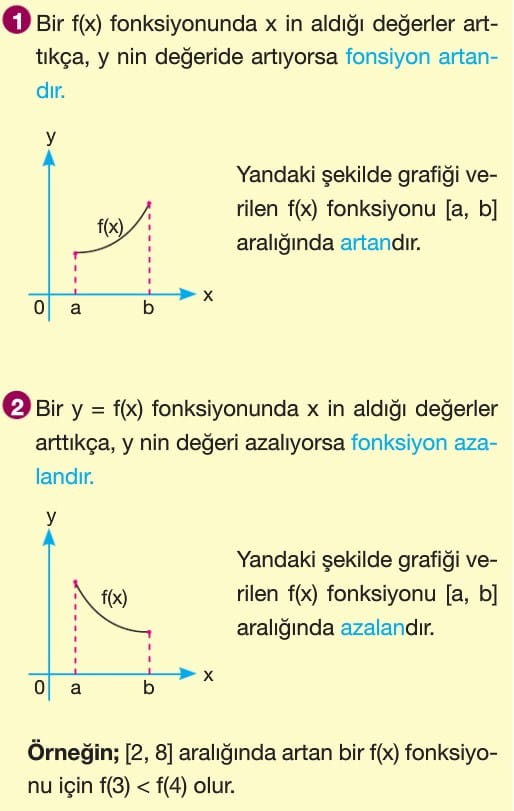
Bir Fonksiyonun Artan ve Azalan Olduğu Aralıklar
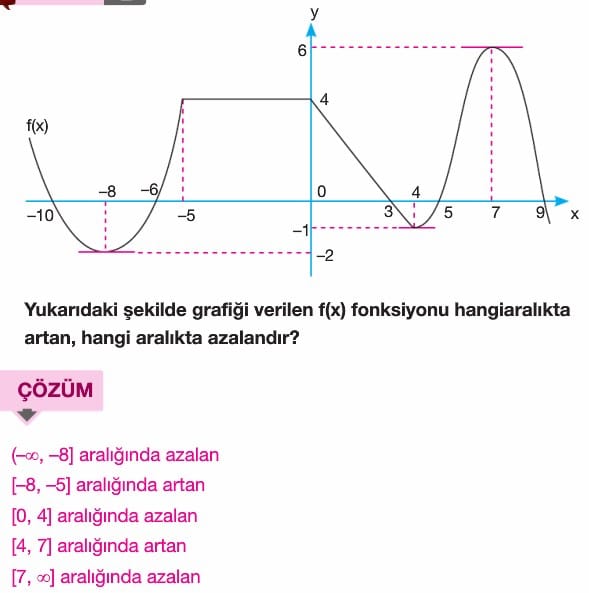
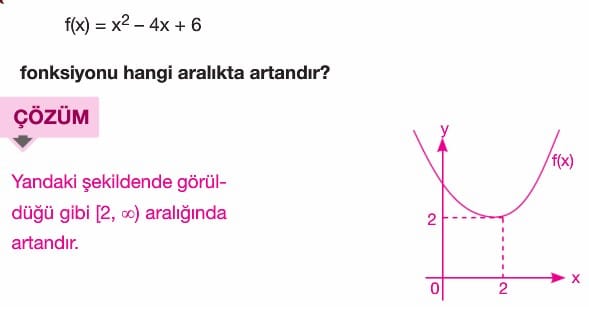
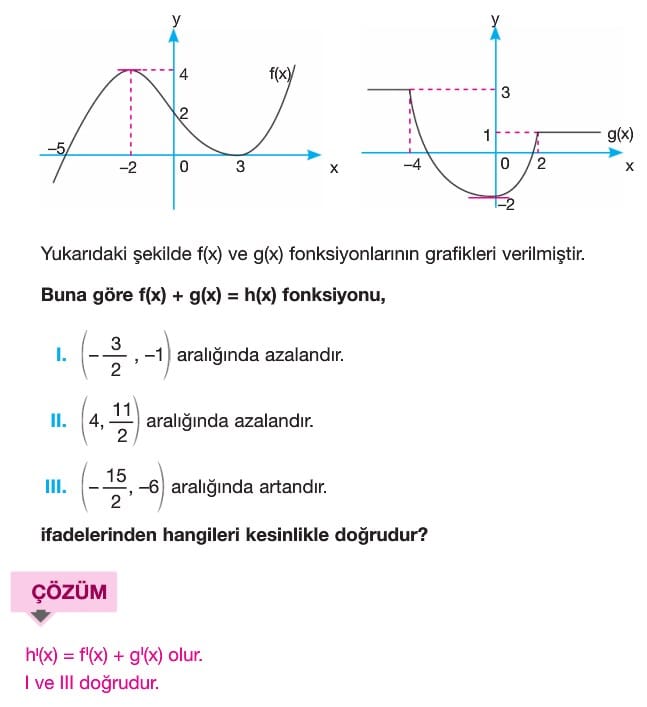
Artan – Azanlık ve Türev İlişkisi
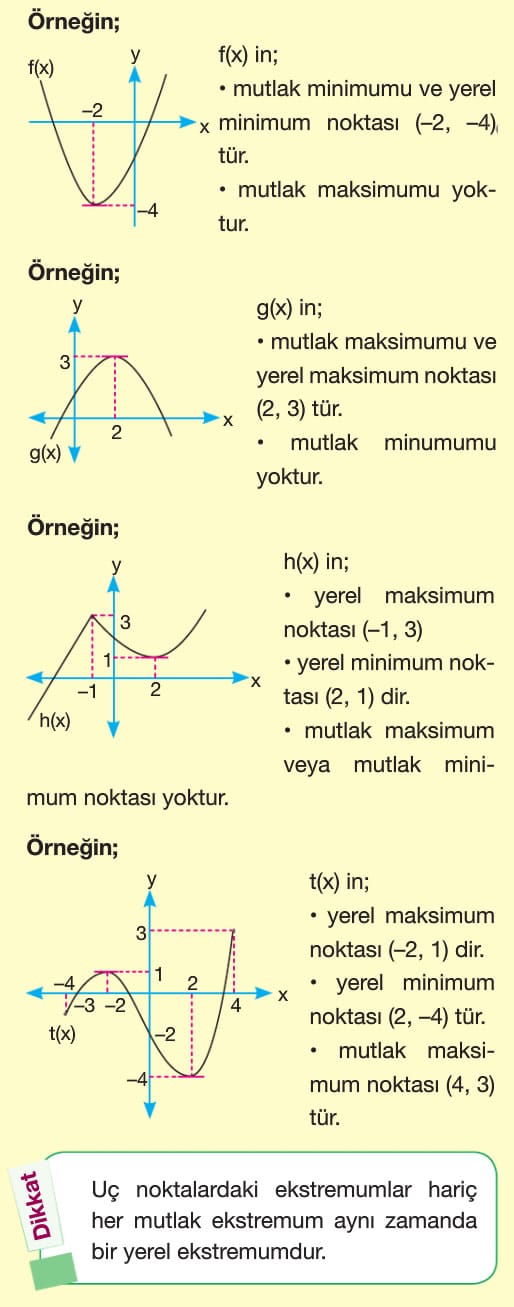
Bir Fonksiyonun Ekstremum Noktaları
Yerel ve Mutlak Ekstremumlar
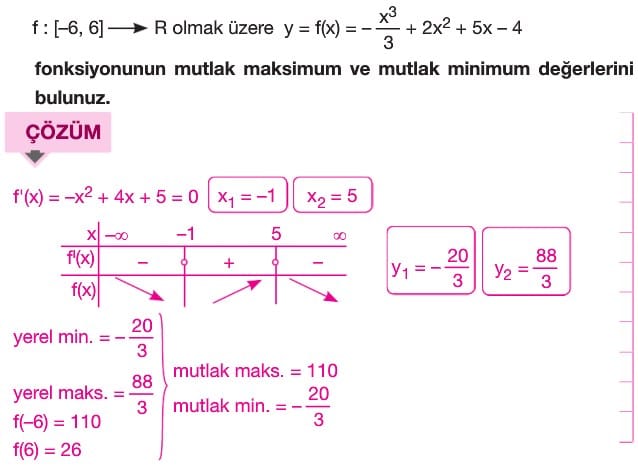
Maksimum ve Minimum Problemleri
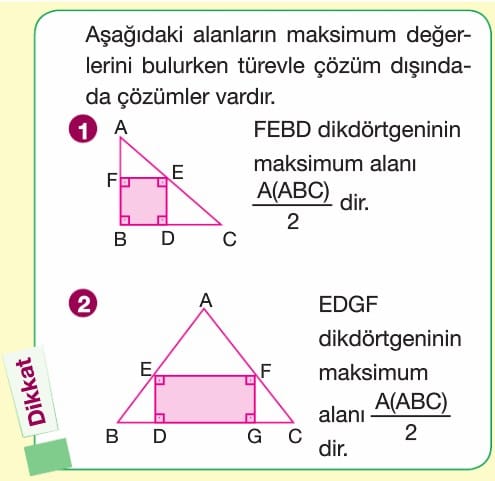
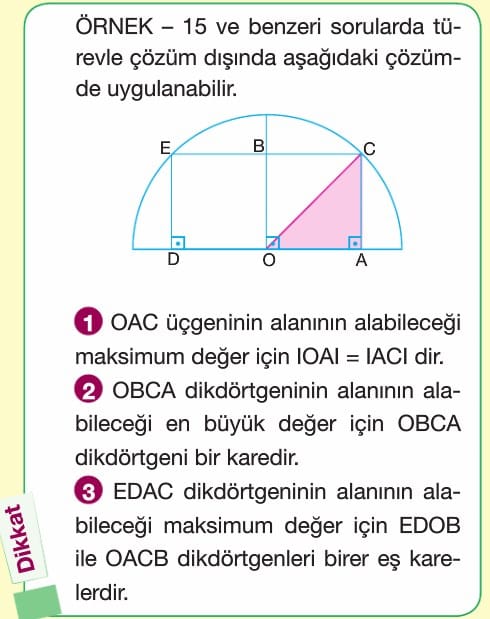
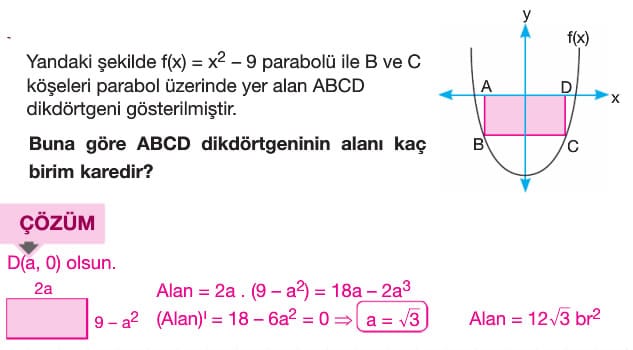
Bir problemde bir ifadenin alabileceği maksimum (veya minimum) değer soruluyorsa öncelikle bu ifadeyi bir fonksiyon olarak ifade etmemiz gerekir. Daha sonra bu fonksiyonun maksimum (veya minimum) değerini bulmak için bu fonksiyonun birinci türevi sıfıra eşitlenir. Oluşan bu denklemdeki köklere göre birinci türevin işaret tablosu yapılıp maksimum (veya minimum) değer bulunur.
Türev Yardımıyla Çizilen Fonksiyon Grafikleri
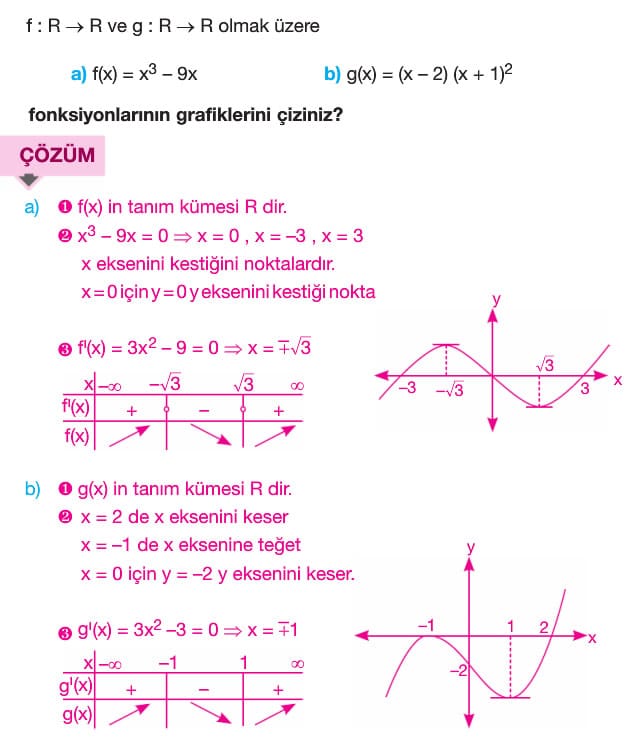
- f(x) bir polinom fonksiyonu olsun. Bu fonksiyonun grafiği çizilirken önce f(x) = 0 denklemi çözülerek varsa x eksenini kestiği noktalar bulunur. Daha sonra f(0) değeri hesaplanarak y eksenini kestiği nokta bulunur. İkinci adımda ise f'(x) türev fonksiyonu yardımıyla fonksiyonun ekstremum noktaları ile artan ve azalan olduğu aralıklara bakılır. Bu bilgiler yardımıyla grafik çizilir.
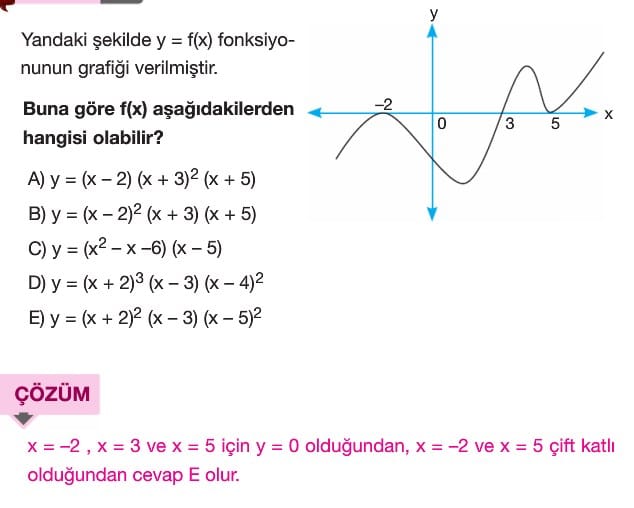
- Grafiği verilen bir fonksiyonun x eksenini kestiği noktalardan biri x1 ise (x – x1) ifadesi fonksiyonunbir çarpanıdır.
Türevin Uygulamaları konu anlatımı soruları çözümleri 12. Sınıf Ayt Matematik
Bir f(x) fonksiyonunda x in aldığı değerler arttıkça, y nin değeri de artıyorsa fonksiyon artan fonksiyondur. Grafiği verilen fonksiyon (a,b) aralığında artandır.
Bir f(x) fonksiyonunda x in aldığı değerler arttıkça, y nin değeri azalıyorsa fonksiyon azalan fonksiyondur. Grafiği verilen fonksiyon (a,b) aralığında azalandır.
Örneğin; [2,8] kapalı aralığında artan bir f(x) fonksiyonu için f(3) < f(4), azalan bir f(x) fonksiyonu için f(3) > f(4) olur.
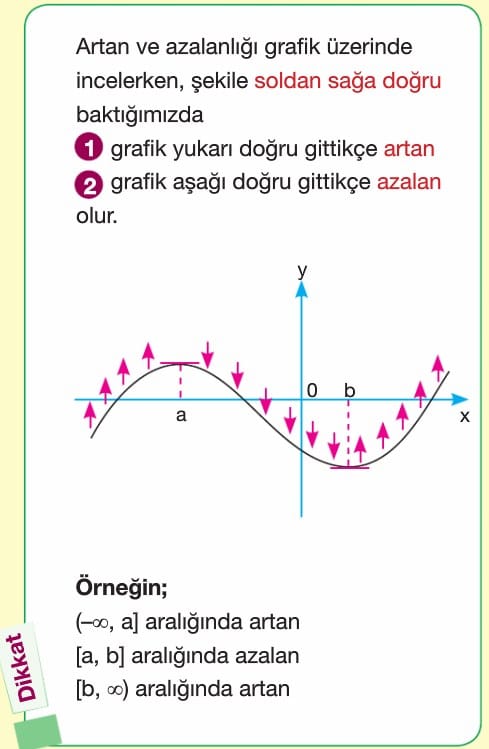
Dikkat: Artan ve azalanlığı grafik üzerinde incelerken soldan sağa doğru baktığımızda; grafik yukarı doğru gittikçe artan, aşağı doğru gittikçe azalan olur.
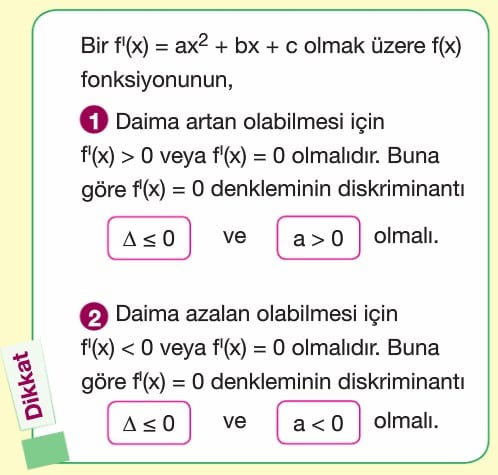
Yandaki şekilde [a,b] aralığında tanımlı, (a,b) aralığında türevli f(x) fonksiyonunun grafiği gösterilmiştir. f(x) in artan olduğu görülmektedir. (a,b) aralığındaki her nokta için f(x) e teğet doğruların eğiminin pozitif olduğu görülmektedir. Dolayısıyla bu aralıkta türev pozitiftir. Yani her (a,b) aralığındaki x elemanı için f'(x) > 0 ise f(x) fonksiyonu [a,b] aralığında artandır.
Yandaki şekilde [a,b] aralığında tanımlı, (a,b) aralığında türevli f(x) fonksiyonunun grafiği gösterilmiştir. f(x) in azalan olduğu görülmektedir. (a,b) aralığındaki her nokta için f(x) e teğet doğruların eğiminin negatif olduğu görülmektedir. Dolayısıyla bu aralıkta türev negatiftir. Yani her (a,b) aralığındaki x elemanı için f'(x) < 0 ise f(x) fonksiyonu [a,b] aralığında azalandır.
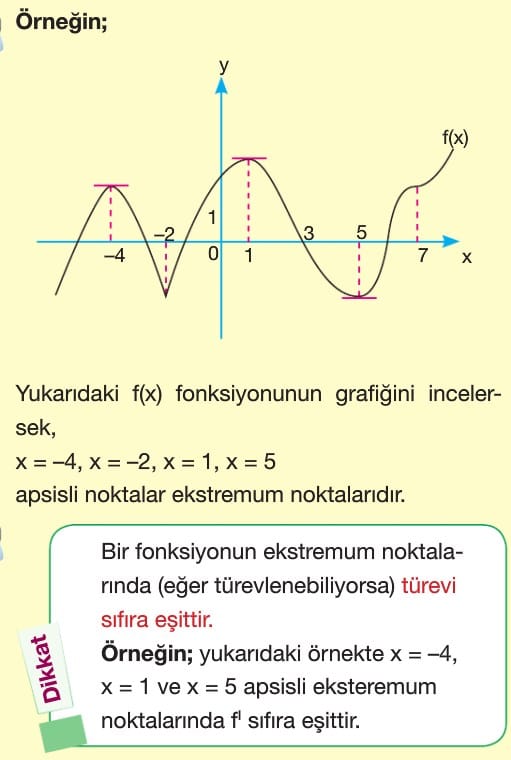
Bir fonksiyonun; artandan azalana geçiş noktasına ve azalandan artana geçiş noktasına fonksiyonun ekstremum noktası denir.
Dikkat: Fonksiyonun tanımlı olduğu aralığın uç noktaları da ekstremum noktası olabilir. İlerleyen bölümlerde daha ayrıntılı işleyeceğiz.
Dikkat: Bir fonksiyonun ekstremum noktalarında (eğer türevlenebiliyorsa) türevi sıfıra eşittir.
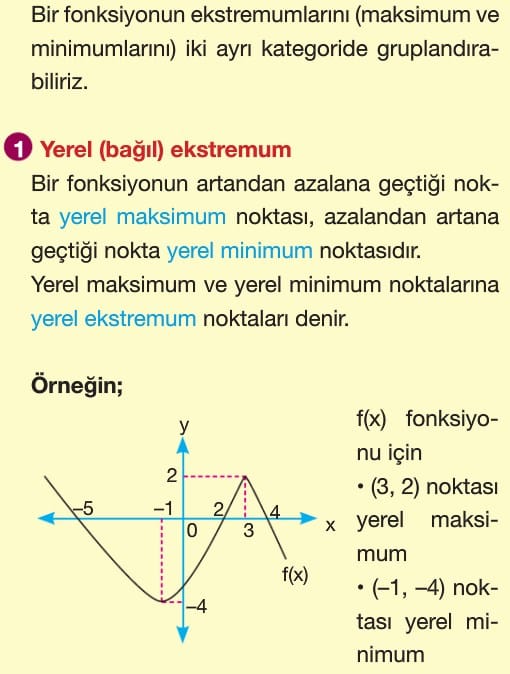
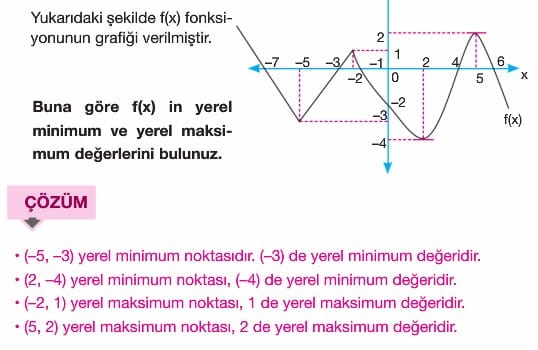
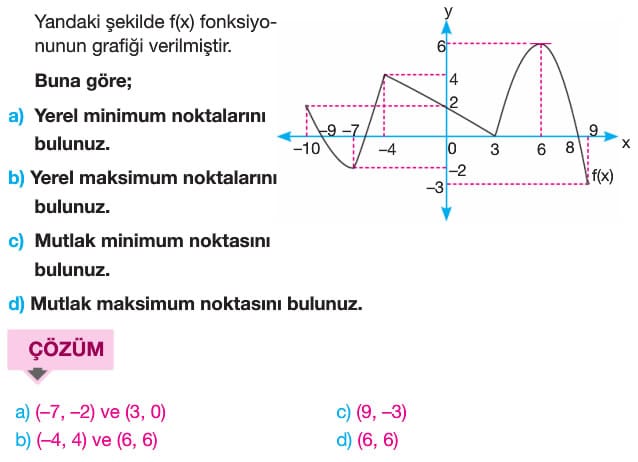
Yerel (Bağıl) ekstremum: Bir fonksiyonun artandan azalana geçtiği nokta yerel maksimum noktası, azalandan artana geçtiği nokta yerel minimum noktasıdır. Yerel maksimum ve yerel minimum noktalarına yerel ekstremum noktaları denir.
Mutlak (Global) Ekstremum: Bir fonksiyonun, tanımlı olduğu aralıkta alabileceği maksimum değeri aldığı nokta mutlak maksimum noktası, alabileceği minimum değeri aldığı nokta mutlak minimum noktasıdır. Mutlak maksimum ve mutlak minimum noktalarına mutlak ekstremum noktaları denir.
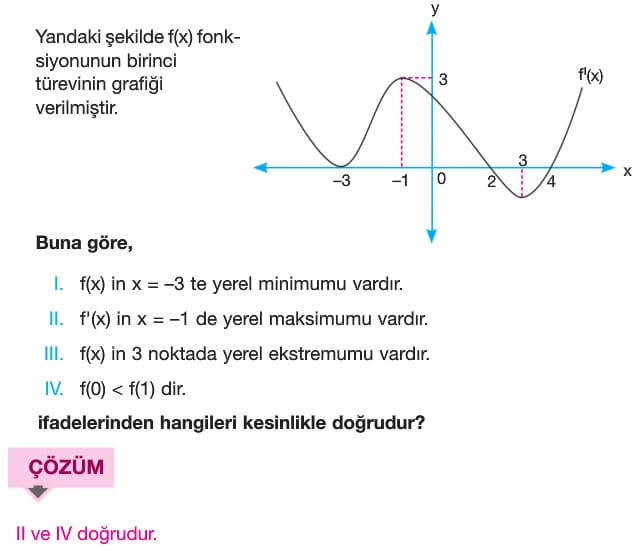
Bir fonksiyonun artandan azalana geçiş noktasının yerel maksimum, azalandan artana geçiş noktasının yerel minimum noktası olduğunu öğrenmiştik. O halde f'(x) fonksiyonunun; pozitif değerden negatif değere geçiş noktası yerel maksimum noktasıdır, negatif değerden, pozitif değere geçiş noktası yerel minimum noktasıdır.









































Trigonometrik ve arc, üstel ve logaritmik fonksiyon ve yüksek mertebeden türev kavramları YKS’nin gelişiyle beraber 2018’de aniden kaldırıldı. Bu konuların 2018 ayt’de yer alması bir istisna idi. 3 yıldır da müfredat matematikte mantık konusu hariç hep aynı diyebiliriz. Yani bu yazıyı müfredata uygun yazmışlar.
Yok zaten o konu bayadır kalktı
konular güncel mi? trigonometrik fonksiyonların türevi neden yok