Bu yazımızda 11. sınıf matematik dersi Trigonometri Ünitesinden Trigonometrik Özdeşlikler konusunun ders notları yer almaktadır. Konu anlatımını bitirdikten sonra 11. Sınıf Trigonometri online testlerini çözebilirsiniz.

11. Sınıf Trigonometri Online Testler

Trigonometrik Özdeşlikler Ders Notu

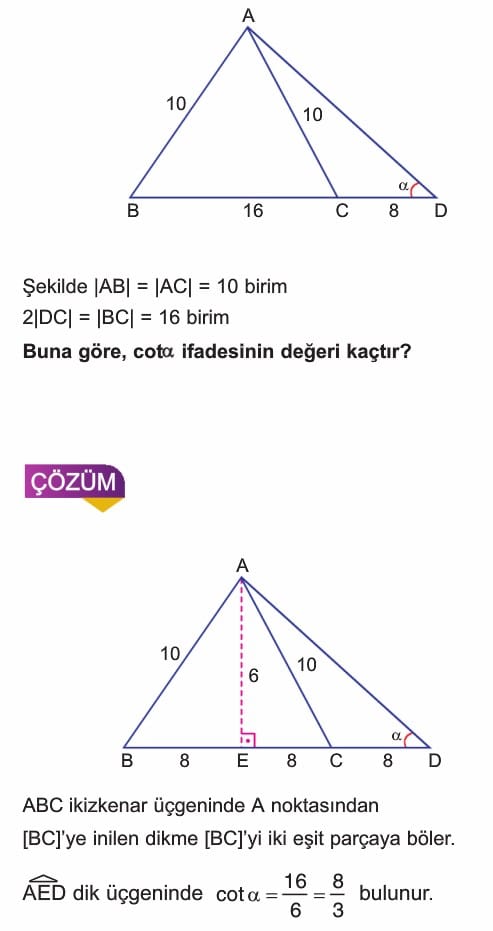
Örnek: 

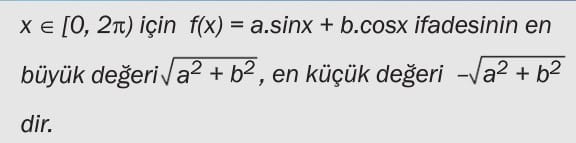
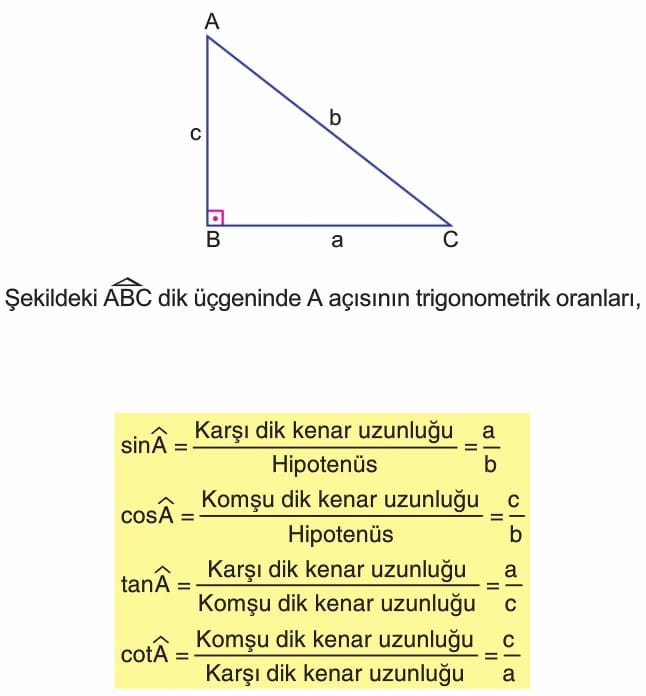
Dar Açıların Trigonometrik Oranları

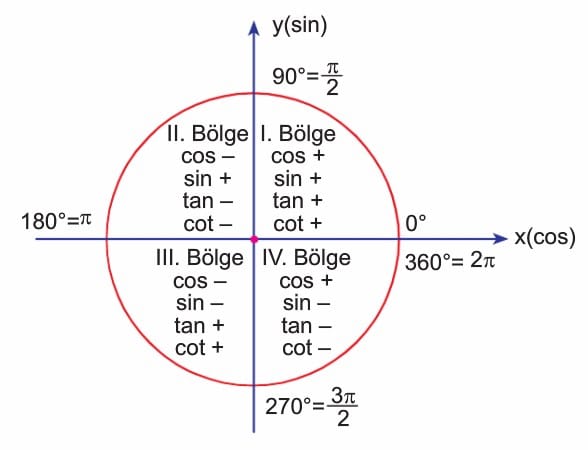
Bölgelere Göre Trigonometrik Fonksiyonların İşareti

Örnek: 

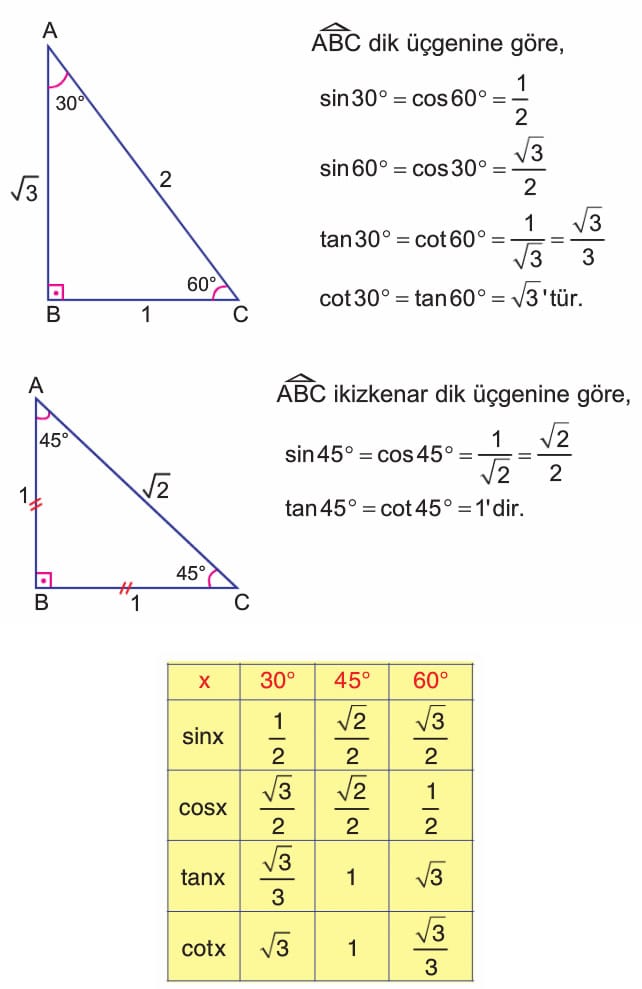
Özel Açıların Trigonometrik Değerleri

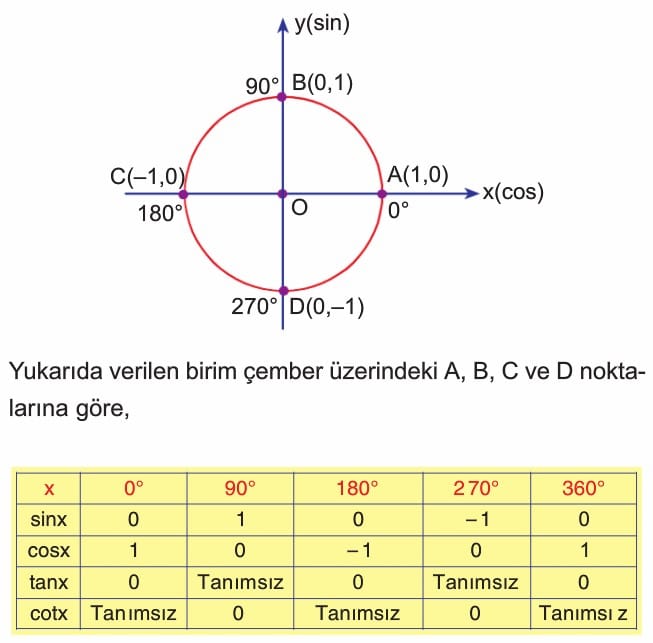
Açıların Bölgelere Göre Trigonometrik Dönüşümü

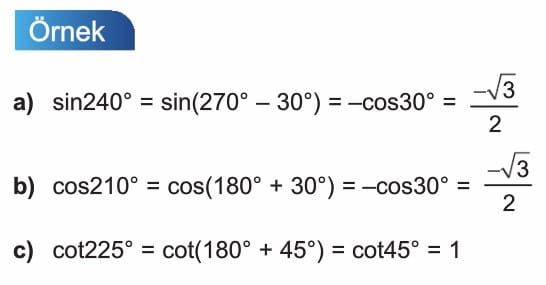
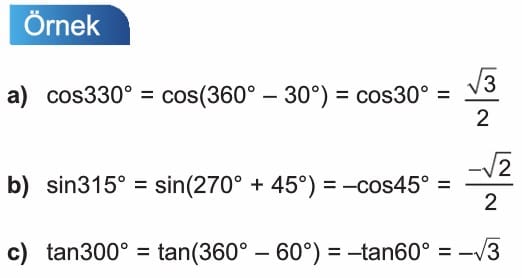
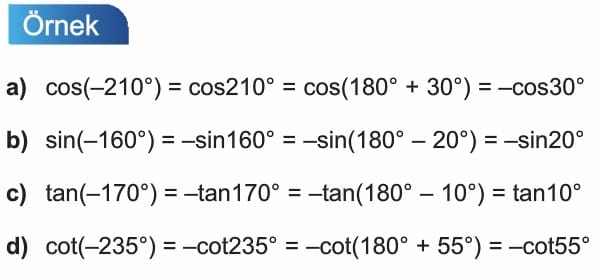
Trigonometrik Özdeşlikler Çözümlü Sorular

1. ÜNİTE: TRİGONOMETRİ

• Yönlü Açılar
• Trigonometrik Fonksiyonlar
• Trigonometrik Özdeşlikler
• Kosinüs Teoremi ve Sinüs Teoremi
• Trigonometrik Fonksiyonların Periyotları
• Trigonometrik Fonksiyonların Grafikleri
• Ters Trigonometrik Fonksiyonlar

---

Trigonometrik Özdeşlikler Çözümlü Test Soruları

Soru 1:
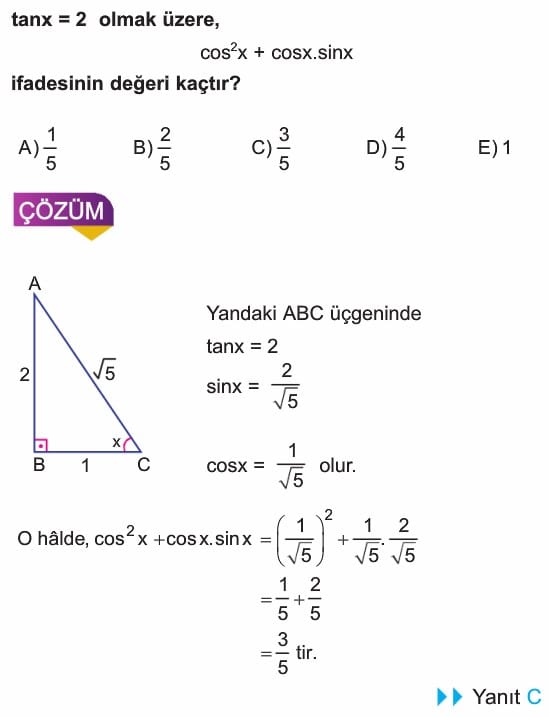
sin²x + cos²x ifadesinin değeri kaçtır?

A) 0
B) 1
C) sin x
D) cos x
E) tan x

Cevap: Trigonometrik özdeşliklerden sin²x + cos²x = 1 olduğundan doğru cevap B şıkkıdır.

---

Soru 2:
tan x = sin x / cos x eşitliği ile ilgili olarak aşağıdaki ifadelerden hangisi doğrudur?

A) tan x çarpanlarına ayrılamaz
B) tan x = cos x / sin x
C) tan x = cot x
D) tan x = sin x / cos x özdeşliğidir
E) tan x = 1

Cevap: tan x = sin x / cos x, temel trigonometrik özdeşliklerden biridir. Doğru cevap D şıkkıdır.

---

Soru 3:
cot x = cos x / sin x ifadesine göre aşağıdakilerden hangisi doğrudur?

A) cot x = tan x
B) cot x çarpanlarına ayrılamaz
C) cot x = cos x
D) cot x = sin x / cos x
E) cot x = cos x / sin x

Cevap: cot x ifadesi cos x / sin x olarak tanımlıdır. Doğru cevap E şıkkıdır.

---

Soru 4:
1 + tan²x = sec²x özdeşliği hangi trigonometrik fonksiyonlar arasında bağlantı kurar?

A) sin ve cos
B) tan ve sec
C) sec ve cos
D) cot ve tan
E) sin ve sec

Cevap: 1 + tan²x = sec²x özdeşliği tan ve sec fonksiyonları arasındaki bağıntıyı verir. Doğru cevap B şıkkıdır.

---

Soru 5:
csc x = 1 / sin x ifadesine göre csc x için aşağıdakilerden hangisi doğrudur?

A) csc x = 1
B) csc x = cos x
C) csc x = 1 / tan x
D) csc x = 1 / sin x
E) csc x = sec x

Cevap: csc x ifadesi sin x’in tersi olarak tanımlıdır, yani csc x = 1 / sin x. Doğru cevap D şıkkıdır.

---

Soru 6:
cos 2x = 1 – 2sin²x eşitliğine göre cos 2x aşağıdaki ifadelerden hangisine eşittir?

A) cos²x – sin²x
B) 2cos²x + 1
C) sin²x – cos²x
D) 2cos x
E) sin 2x

Cevap: cos 2x = cos²x – sin²x olarak da ifade edilebilir. Doğru cevap A şıkkıdır.

---

Soru 7:
tan 2x = 2tan x / (1 – tan²x) ifadesi hangi trigonometrik dönüşümün sonucudur?

A) Cosine formülü
B) Sine formülü
C) Çift açılı tanjant formülü
D) Ters trigonometrik oranlar
E) Çift açılı cotanjant formülü

Cevap: Bu ifade çift açılı tanjant formülüdür. Doğru cevap C şıkkıdır.

koordinatları birim çember üzerinde ölçüsü sırasıyla G, (r: – O), (rc + 6) ve (2rc- 6), (-6) olan açıların bitim kollarının çembere değdiği noktalardır olarak yazılabilir. Verilen özdeşlikler incelendiğinde

+ 9, 211 – 9 geçişlerinde fonksiyonun ismi değişmemekte, bulunduğu bölgeye göre işareti değişebilmektedir. Trigonometrik fonksiyonların işaretleri hatırlanmalıdır. Ayrıca IV nolu özdeşlik grubu incelendiğinde cos(-9) = cose olduğu için kosinüs fonksiyonunun bir çift fonksiyon, diğerlerinin (tan, cot, sin) tek fonksiyon olduğu görülmektedir.

Çözüm: yapılırken önce verilen ifadenin pozitif ya da negatif olduğuna bakıldığına ve daha sonra (180 – a), (180 + a) veya (360 – a), (-0c) geçişlerinde fonksiyonun ismi değiştirilmeden birinci bölgedeki özdeşiyle adlandırıldığına ve sonra işaretinin yazıldığına dikkat ediniz. sin 210° 210° 3. bölgede olduğu için bu bölgede sinüs değeri (-) olacaktır. Yani 210° = 180° + 30° olduğundan birinci bölgedeki 30 ile eşleştirilmeli ve sin 210° = -sin 30° yazılmalıdır.

Örnek: tan 240° . cos 300° + cot 120° . sin 240° ifadesinin sonucunu bulalım.

Çözüm
Bu oranların işaretlerini belirleyip birinci bölgedeki uygun oranla eşlemeliyiz.
tan 240° = tan (270° – 30°) = cot 30°
cos 300° = cos (270° + 30°) = sin 30°
cot 120° = cot (90° + 30°) = -tan30°
sin 240° = sin (270° – 30°) = -c0s30°
tan 240° . cos 300° + cot 120° . sin 240°
cot 30° . sin 30° + (-tan 30°) (-cos 30°)

Örnek:
sin 70° = a olduğuna göre, cos 200° . sin 160° ifadesinin a cinsinden eşitini bulalım.
Çözüm:
sin 200° ün işareti negatiftir.
sin 160° ın işareti pozitifiir.
cos 200° = cos (180° + 20°)
= -cos 20°
sin 160° = sin (180°- 20°)
= sin 20°
sin 70° = a olduğundan toplamları 90° olan iki açıdan birinin sinüsü diğerinin kosinûse eşit olduğundan
cos 20° = sin 70° = adır.
sin 20° = cos 70° olduğu bilindiği için