Trigonometrik fonksiyonların grafikleri, aşağıda verilen işlem sırasına göre çizilebilir.

• Fonksiyonun periyodu bulunur.
• Bulunan periyoda uygun aralık seçilir.
• Seçilen aralıkta fonksiyonun değişim tablosu yapılır.
• Seçilen aralık değişim tablosuna uygun olarak fonksiyonun grafiği çizilir.

Kosinüs Fonksiyonunun Grafiği

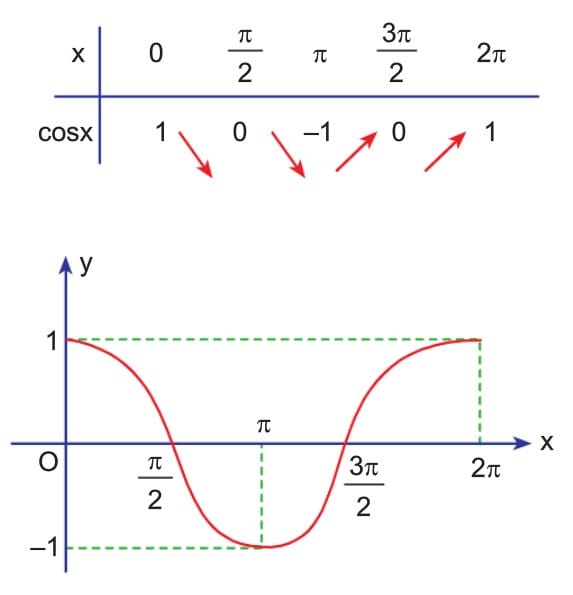
f(x) = cosx fonksiyonunun periyodu 2π dir. [0, 2π] aralığında fonksiyonun değişim tablosunu yaparak grafiği çizelim.

Sinüs Fonksiyonunun Grafiği

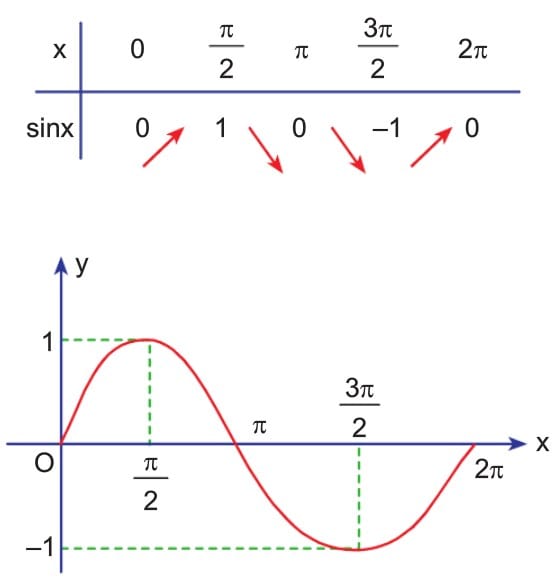
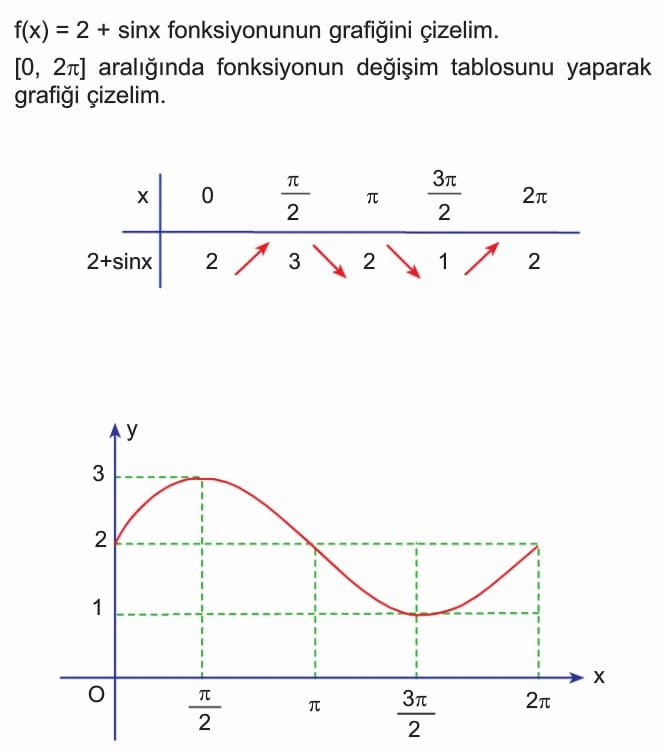
f(x) = sinx fonksiyonunun periyodu 2π dir. [0, 2π] aralığında fonksiyonun değişim tablosunu yaparak grafiği çizelim.

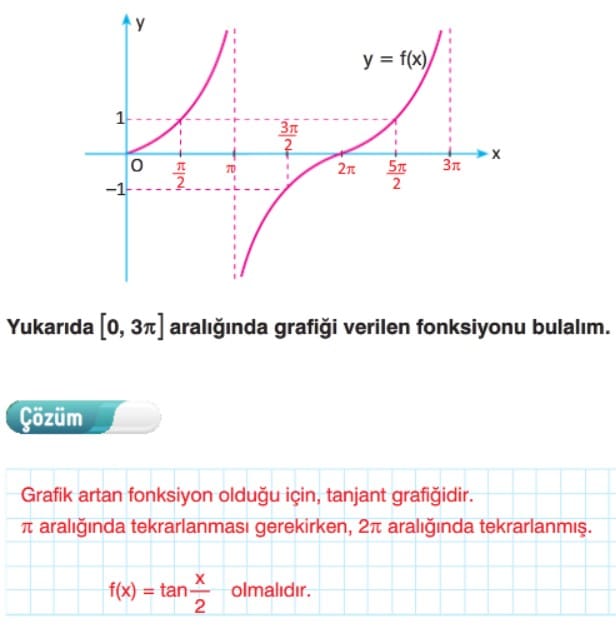
Tanjant Fonksiyonunun Grafiği

f(x) = tanx fonksiyonunun periyodu π’dir. f(x) = tanx fonksiyonu x = π/2 değerinde tanımsız oldugundan grafik x = π/2 doğrusunu kesmez.
[0, π] – {π/2} aralığında fonksiyonun değişim tablosunu yaparak grafiği çizelim.

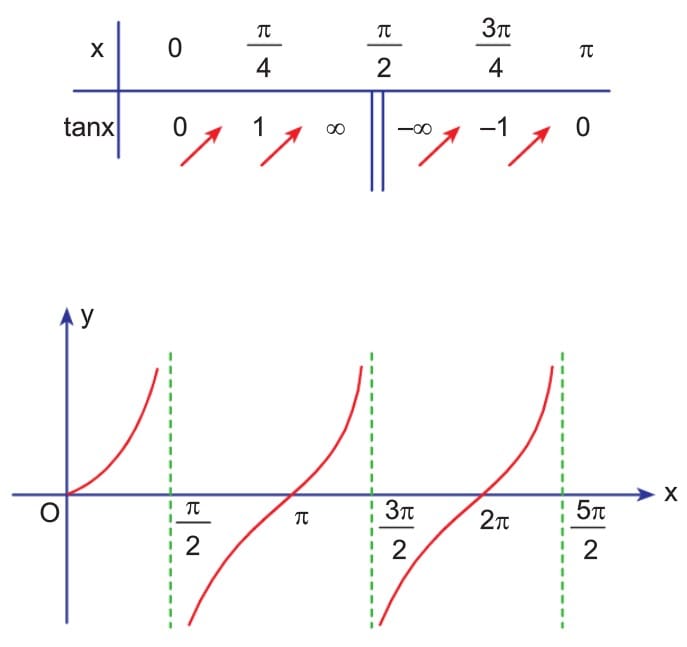
Uyarı: Yukarıdaki grafikte görüldüğü gibi, oluşan grafik diğer periyodik aralıklarda tekrarlanarak fonksiyonun genel grafiği çizilebilir.

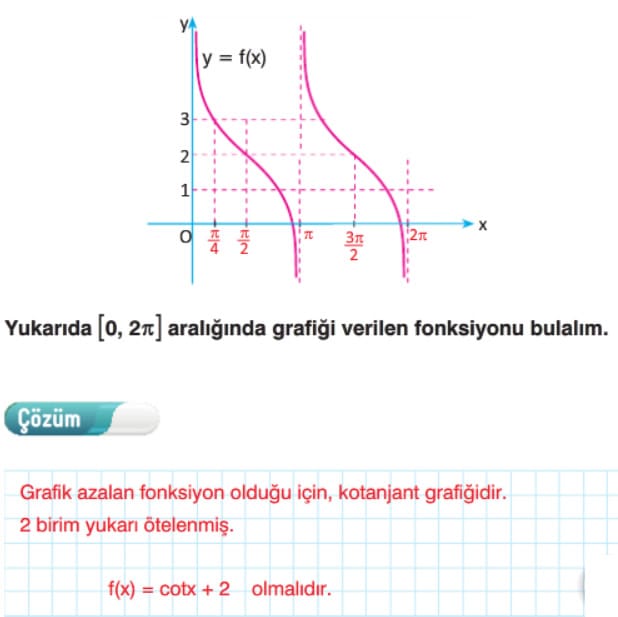
Kotanjant Fonksiyonunun Grafiği

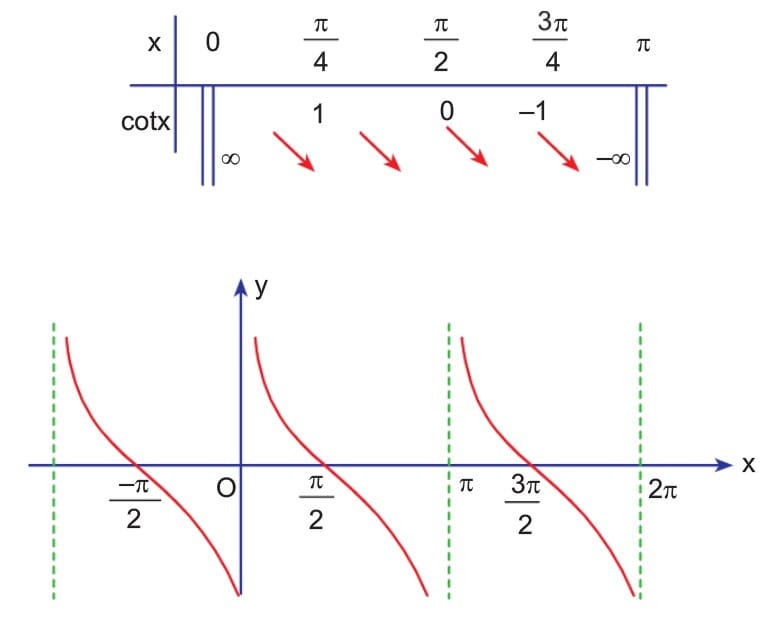
f(x) = cotx fonksiyonunun periyodu π’dir. f(x) = cotx fonksiyonu x = 0 ve x = π değerlerinde tanımsız oldugundan grafik, x = 0 ve x = π doğrularını kesmez.
[0, π] – {0, π} aralığında fonksiyonun değişim tablosunu yaparak grafiği çizelim.

Trigonometrik Fonksiyonların Grafikleri Çözümlü Sorular

Çözümlü Örnek Sorular

Soru 1
f(x) = sin(x) fonksiyonunun [0, 2π] aralığındaki grafiğini çiziniz. Fonksiyonun maksimum, minimum ve kesişim noktalarını belirleyiniz.

Çözüm:

• f(x) = sin(x) fonksiyonu [0, 2π] aralığında tanımlıdır.
• Maksimum değeri: 1 (x = π/2 noktasında)
• Minimum değeri: -1 (x = 3π/2 noktasında)
• Kesişim noktaları: (0, 0), (π, 0), (2π, 0)

Cevap: Bu bilgileri kullanarak sin(x) fonksiyonunun grafiğini çizebilirsiniz.

Soru 2
g(x) = cos(x) fonksiyonunun [0, 2π] aralığındaki grafiğini çiziniz ve bu aralıktaki maksimum, minimum değerleri bulunuz.

Çözüm:

• g(x) = cos(x) fonksiyonu [0, 2π] aralığında tanımlıdır.
• Maksimum değeri: 1 (x = 0 ve x = 2π noktasında)
• Minimum değeri: -1 (x = π noktasında)
• Kesişim noktaları: (π/2, 0) ve (3π/2, 0)

Cevap: Bu bilgilere göre cos(x) fonksiyonunun grafiğini çizebilirsiniz.

Soru 3
h(x) = tan(x) fonksiyonunun (-π/2, π/2) aralığındaki grafiğini çiziniz ve asimptot noktalarını belirtiniz.

Çözüm:

• h(x) = tan(x) fonksiyonu, x = -π/2 ve x = π/2 noktalarında tanımsızdır (dikey asimptot).
• Bu aralıkta tan(x) grafiği -∞ ile ∞ arasında değer alır ve asimptot çizgileri x = -π/2 ve x = π/2 doğrularıdır.

Cevap: Tan(x) fonksiyonunun bu aralıktaki grafiğinde asimptotları gösterin.

Soru 4
f(x) = 2sin(x) fonksiyonunun [0, 2π] aralığındaki grafiğini çiziniz ve genliğini belirtiniz.

Çözüm:

• f(x) = 2sin(x) fonksiyonunun genliği 2’dir.
• Bu fonksiyonun maksimum değeri 2 ve minimum değeri -2’dir.
• Kesişim noktaları sin(x) fonksiyonundaki ile aynıdır: (0, 0), (π, 0), (2π, 0)

Cevap: 2sin(x) fonksiyonunun grafiğini çizerek genliği gösterin.

Soru 5
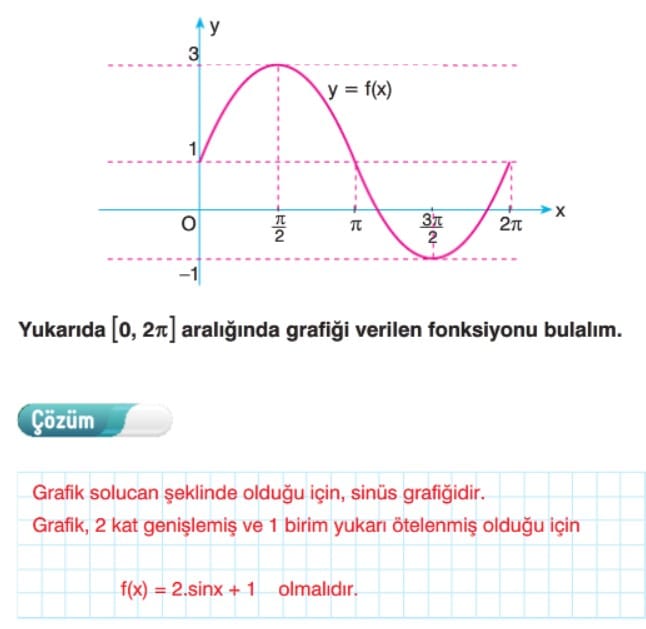
y = sin(x) + 1 fonksiyonunun [0, 2π] aralığındaki grafiğini çiziniz. Bu fonksiyonun en küçük ve en büyük değerini bulunuz.

Çözüm:

• y = sin(x) + 1 fonksiyonunun grafiği sin(x) grafiğinin 1 birim yukarıya kaydırılmış halidir.
• En küçük değer: 0 (x = 3π/2)
• En büyük değer: 2 (x = π/2)

Cevap: Bu bilgilere göre sin(x) + 1 fonksiyonunun grafiğini çizebilirsiniz.

Soru 6
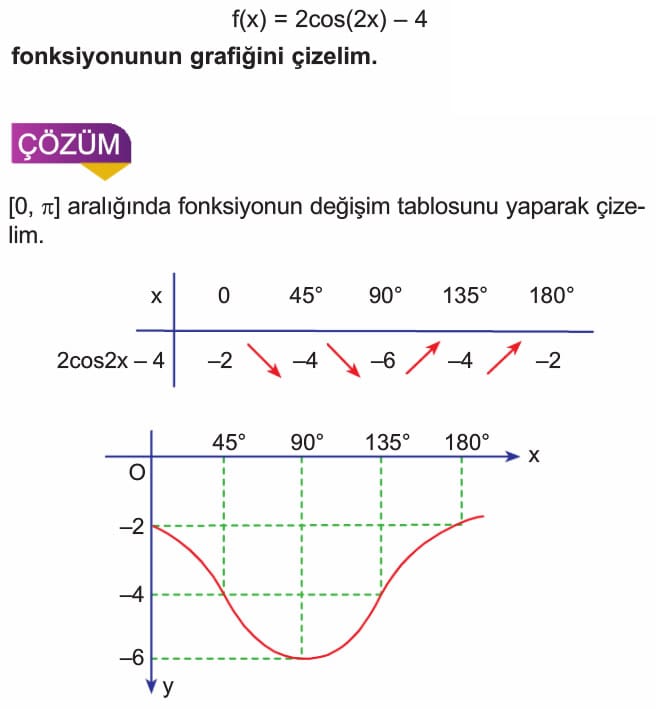
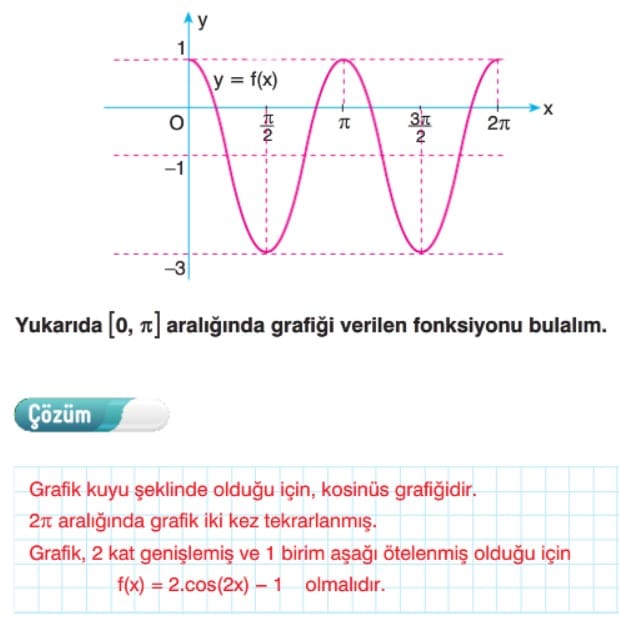
y = cos(2x) fonksiyonunun [0, π] aralığındaki grafiğini çiziniz ve periyodunu belirtiniz.

Çözüm:

• y = cos(2x) fonksiyonunun periyodu, normal cos(x) fonksiyonunun periyodunun yarısıdır: T = π.
• Bu fonksiyon [0, π] aralığında bir tam döngü yapar.
• Maksimum değeri 1, minimum değeri -1’dir.

Cevap: Cos(2x) fonksiyonunun [0, π] aralığındaki grafiğini çizerek periyodunu gösterin.

Hatırlatma: Her x gerçek sayısı için f(-x) = f(x) ise f fonksiyonuna çift fonksiyon denir. Her x gerçek sayısı için için f(-x) = -f(x) ise f fonksiyonuna tek fonksiyon denir. Çift fonksiyonlar y eksenine göre simetriktir. Tek fonksiyonlar orijine göre simetriktir. sinx fonksiyonunun grafiği incelendiğinde, grafiğin orijine göre simetrik olduğu görülür. sinx fonksiyonu tek fonksiyondur. alfa gerçek sayısı için sin(-alfa) = -sinalfa dır.

Örnek: sin(a – b) + sin(b – a) toplamını bulalım.
Çözüm: sinüs fonksiyonu tek fonksiyon olduğundan
sin(a – b) = -sin(b – a) dır. dolayısıyla sin(a – b) + sin(b – a) = -sin(b – a) + sin(b – a) = 0 olur.

cosx fonksiyonunun grafiği incelendiğinde, grafiğin y eksenine göre simetrik olduğu görülecektir. cosx fonksiyonu çift fonksiyondur.
Her x gerçek sayısı için cos(-alfa) = cos alfa dır.

Örnek: cos(140° – ß) – cos(ß + 220°) toplamını bulalım.
Çözüm: Birim çember üzerinde 220° = -140° olduğu düşünülürse ifade cos(140° – ß) – cos(ß -140°) olur. cosinüs fonksiyonu çift fonksiyon olduğundan
cos(140°- ß) = cos(ß -140°) tır.
cos(140° – ß) – cos(ß -140°) = 0 olur.
tanx ve cofx fonksiyonlarının grafikleri incelendiğinde grafiklerin orijine göre simetrik oldukları görülür. tanx fonksiyonu ve cotx fonksiyonu birer tek fonksiyondur. Her x gerçek sayısı için tan(-x) = -tanx ve cot(-x) = -cotx tir.

Trigonometrik fonksiyonların grafikleri çizilirken önce fonksiyonun esas periyodu bulunur. Sonra periyot uzunluğunda bir aralık seçilip fonksiyonun bu aralıkta bulunabilecek değerleri için bir değişim tablosu oluşturur. Değişim tablosundaki noktalar koordinat düzlemine yerleştirilerek grafik çizilir. Periyot uzunluğundaki tüm aralıklarda oluşan grafik tekrarlanır.

Hatırlatma: Her x gerçek sayısı için f(-x) = f(x) ise f fonksiyonuna çift fonksiyon denir. Her x gerçek sayısı için için f(-x) = -f(x) ise f fonksiyonuna tek fonksiyon denir. Çift fonksiyonlar y eksenine göre simetriktir. Tek fonksiyonlar orijine göre simetriktir. sinx fonksiyonunun grafiği incelendiğinde, grafiğin orijine göre simetrik olduğu görülür. sinx fonksiyonu tek fonksiyondur. alfa gerçek sayısı için sin(-alfa) = -sinalfa dır.

Örnek: sin(a – b) + sin(b – a) toplamını bulalım.
Çözüm: sinüs fonksiyonu tek fonksiyon olduğundan
sin(a – b) = -sin(b – a) dır. dolayısıyla sin(a – b) + sin(b – a) = -sin(b – a) + sin(b – a) = 0 olur.

cosx fonksiyonunun grafiği incelendiğinde, grafiğin y eksenine göre simetrik olduğu görülecektir. cosx fonksiyonu çift fonksiyondur.
Her x gerçek sayısı için cos(-alfa) = cos alfa dır.

Örnek: cos(140° – ß) – cos(ß + 220°) toplamını bulalım.
Çözüm: Birim çember üzerinde 220° = -140° olduğu düşünülürse ifade cos(140° – ß) – cos(ß -140°) olur. cosinüs fonksiyonu çift fonksiyon olduğundan
cos(140°- ß) = cos(ß -140°) tır.
cos(140° – ß) – cos(ß -140°) = 0 olur.
tanx ve cofx fonksiyonlarının grafikleri incelendiğinde grafiklerin orijine göre simetrik oldukları görülür. tanx fonksiyonu ve cotx fonksiyonu birer tek fonksiyondur. Her x gerçek sayısı için tan(-x) = -tanx ve cot(-x) = -cotx tir.

Trigonometrik fonksiyonların grafikleri çizilirken önce fonksiyonun esas periyodu bulunur. Sonra periyot uzunluğunda bir aralık seçilip fonksiyonun bu aralıkta bulunabilecek değerleri için bir değişim tablosu oluşturur. Değişim tablosundaki noktalar koordinat düzlemine yerleştirilerek grafik çizilir. Periyot uzunluğundaki tüm aralıklarda oluşan grafik tekrarlanır.