Trigonometrik Fonksiyonlar 11. sınıf

Sinüs ve Kosinüs Fonksiyonları

Çözümlü Sorular
Bölgelere Göre Sinüs ve Kosinüs Fonksiyonları
A. Kosinüs Fonksiyonu
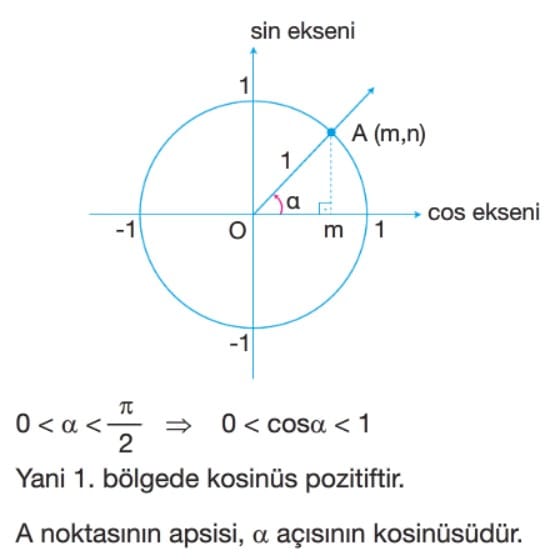
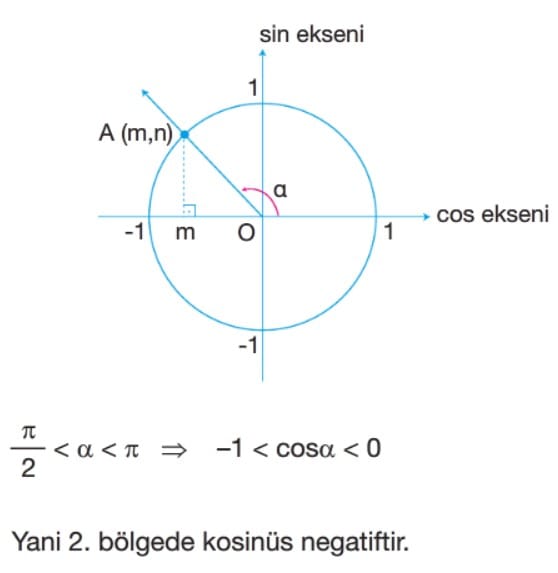
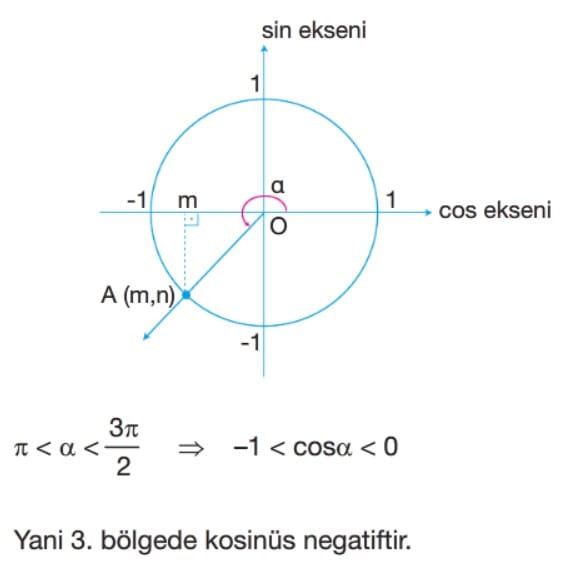
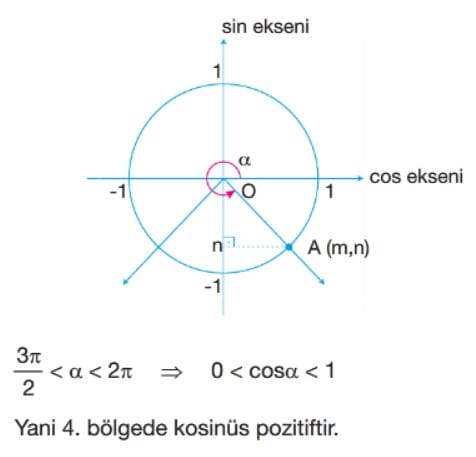
Kosinüs Fonksiyonunun İndirgenmesi

B. Sinüs Fonksiyonu
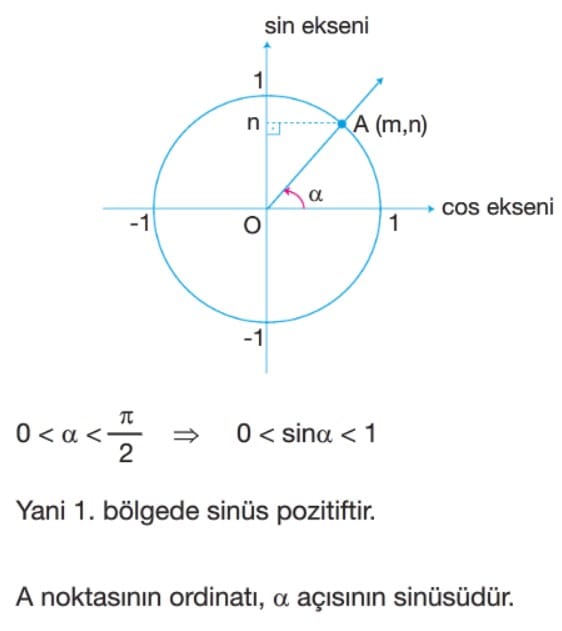
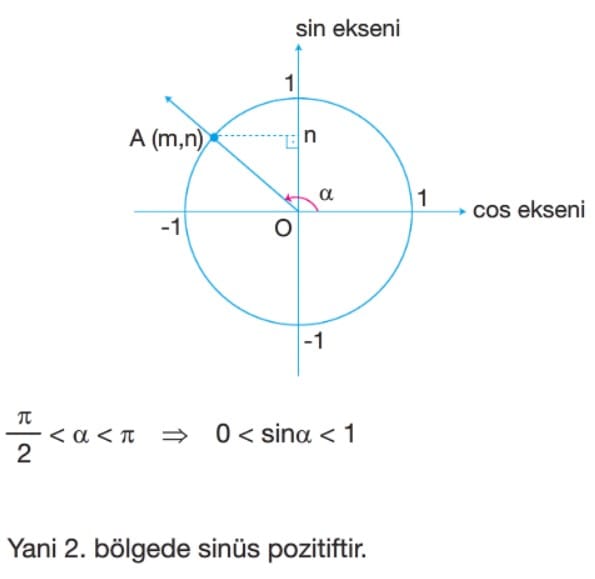
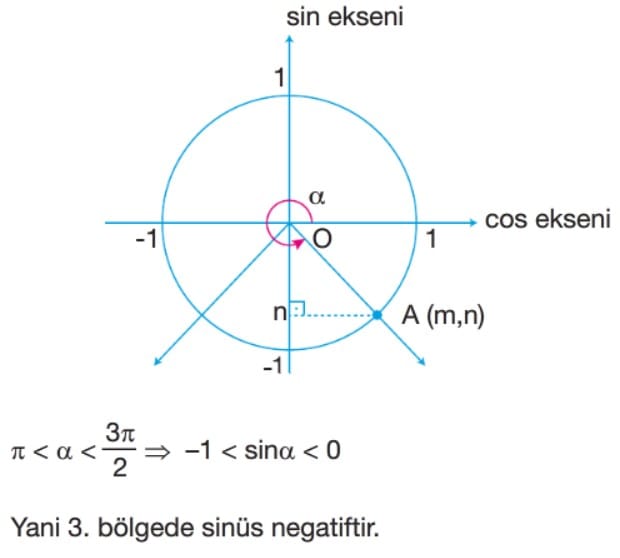
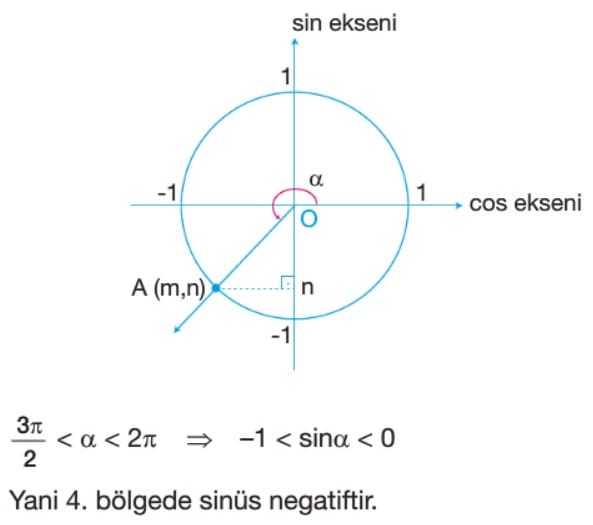

Sinüs Fonksiyonun İndirgenmesi

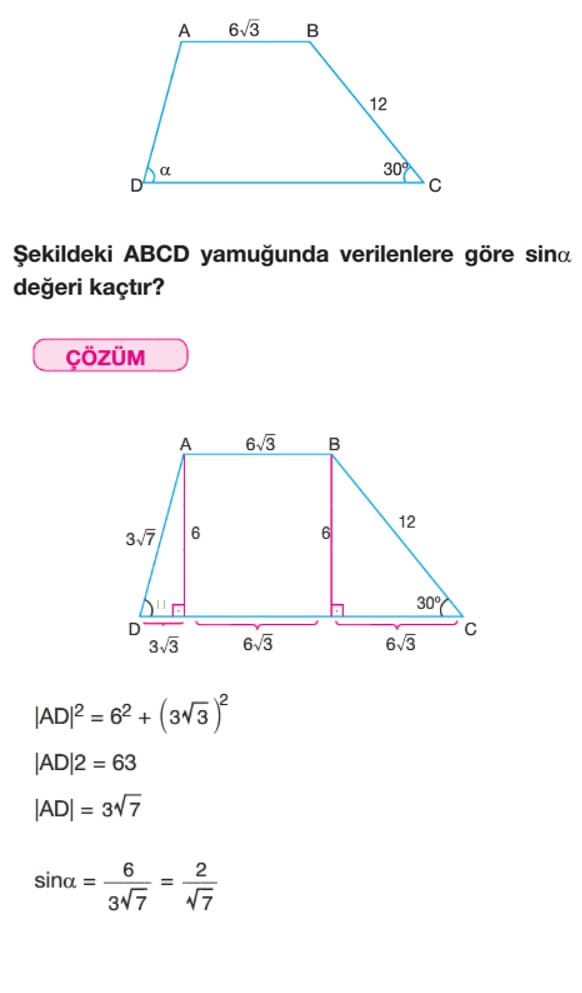
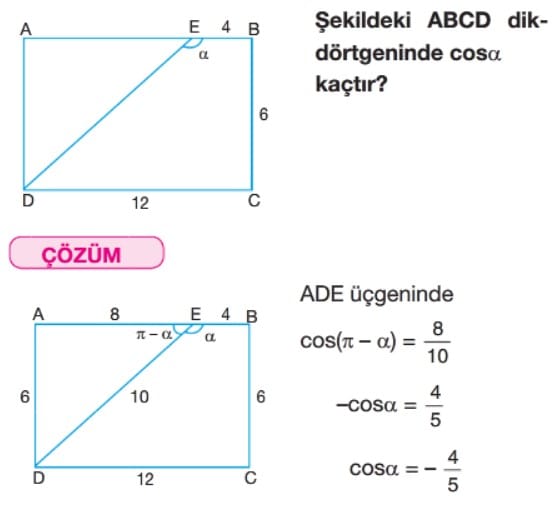
Sinüs ve Kosinüs Fonksiyonu Çözümlü Sorular
C. Tanjant Fonksiyonu

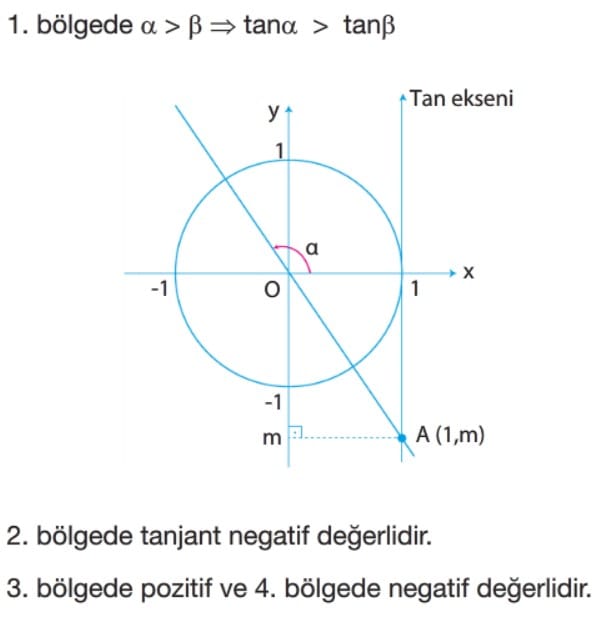
Tanjant Fonksiyonunun İndirgenmesi
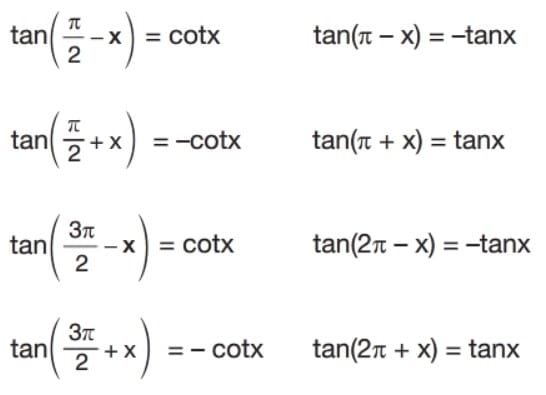
D. Kotanjant Fonksiyonu
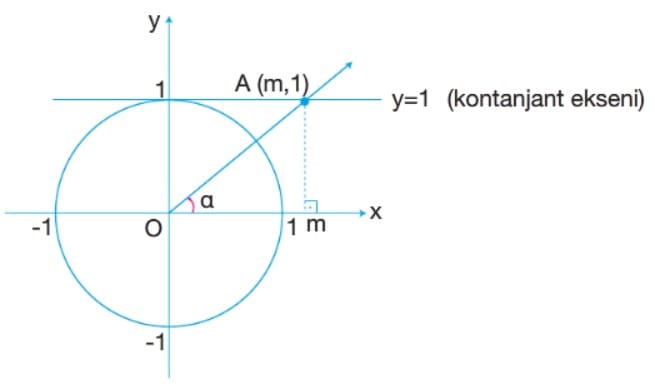

Kotanjant Fonksiyonunun İndirgenmesi
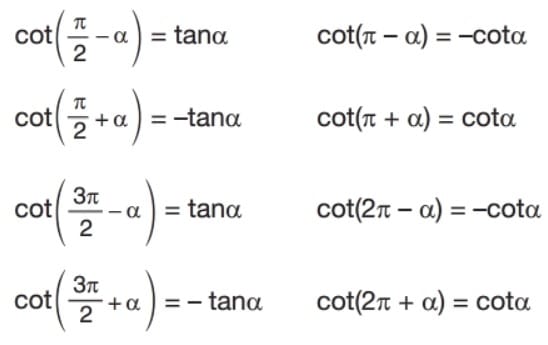
Tanjant ve Kotanjant Fonksiyonu Çözümlü Sorular
Dik Üçgende Dar Açıların Trigonometrik Oranları
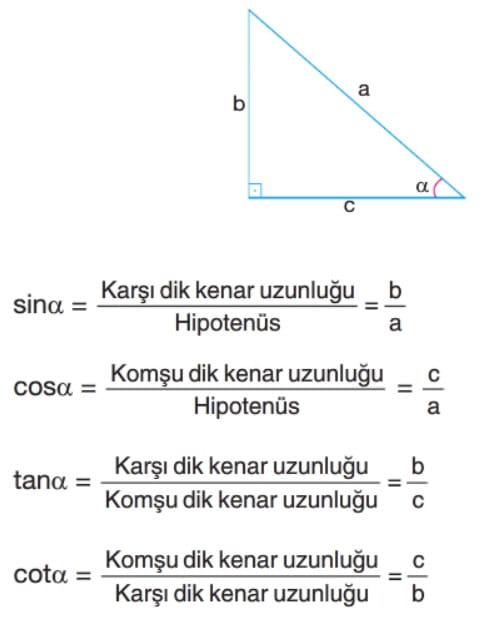
Dik Üçgende Dar Açıların Trigonometrik Oranları Çözümlü Sorular
Özel Açıların Trigonometrik Oranları


Özel Açıların Trigonometrik Oranları Çözümlü Sorular
Çözümlü Örnek Test Soruları: Trigonometrik Fonksiyonlar
Soru 1:
sin(30°) değeri kaçtır?
a) 1
b) 0,5
c) √2/2
d) √3/2
Çözüm: sin(30°) = 0,5 olarak bilinir. Cevap: b)
Soru 2:
cos(60°) değeri kaçtır?
a) 0,5
b) √3/2
c) 1
d) 0
Çözüm: cos(60°) = 0,5 olarak bilinir. Cevap: a)
Soru 3:
tan(45°) değeri kaçtır?
a) 0
b) 1
c) √3
d) √2
Çözüm: tan(45°) = 1 olarak bilinir. Cevap: b)
Soru 4:
cot(90°) değeri kaçtır?
a) 1
b) 0
c) Sonsuz
d) √3
Çözüm: cot(90°) değeri tanımsızdır ve sonsuz olarak kabul edilir. Cevap: c)
Soru 5:
sin(0°) değeri nedir?
a) 1
b) 0
c) √2/2
d) √3/2
Çözüm: sin(0°) = 0 olarak bilinir. Cevap: b)
Soru 6:
cos(90°) değeri nedir?
a) 0
b) 1
c) -1
d) √3/2
Çözüm: cos(90°) = 0 olarak bilinir. Cevap: a)
Soru 7:
tan(0°) değeri kaçtır?
a) 0
b) 1
c) Sonsuz
d) -1
Çözüm: tan(0°) = 0 olarak bilinir. Cevap: a)
Soru 8:
sin(45°) değeri kaçtır?
a) 1
b) 0
c) √2/2
d) √3/2
Çözüm: sin(45°) = √2/2 olarak bilinir. Cevap: c)
Alfa açısının bitim kenarının birim çemberi kestiği P noktasının koordinatları P(x, y) olmak üzere P noktasının apsisine alfa açısının kosinüsü denir.
x = cosalfa şeklinde gösterilir. alfa açısını cosalfa yapan fonksiyona kosinüs fonksiyonu denir.
alfa açısının bitim kenarının birim çemberi kestiği P noktasının koordinatları P(x, y) olmak üzere P noktasının ordinatına alfa açısının sinüsü denir. y =sinalfa şeklinde gösterilir. alfa açısını sinalfa yapan fonksiyona sinüs fonksiyonu denir.
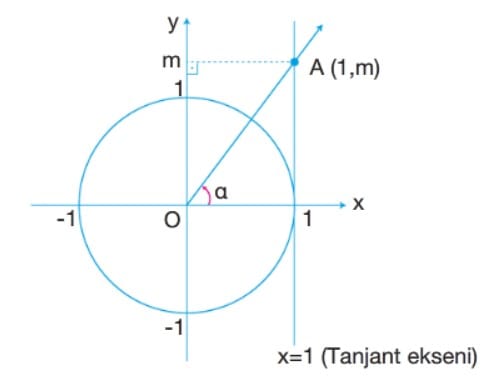
Bir alfa açısının bitim kolunun x = 1 doğrusu ile kesiştiği T noktasının ordinatına alfa açısının tanjantı denir ve tanalfa ile gösterilir. tanjant ekseni alfa reel sayısını tanalfa ile eşleştiren fonksiyona tanjant fonksiyonu denir.
alfa açısının çemberi kestiği P noktasından çizilen teğetin x eksenini kestiği D noktasının apsisine alfa açısının sekantı denir ve secalfa
ile gösterilir.
oı açısının çemberi kestiği P noktasından çizilen teğetin eksenini kestiği D noktasının ordinatına alfa açısının kosekantı
denir ve cosecalfa ile gösterilir. A ve A’ noktalarından çizilen teğet y eksenine paralel olduğu için y ekseni ile kesişmez o yüzden cosec(0) ve cosec(pi), cosec(2 pi) tanımsızdır.
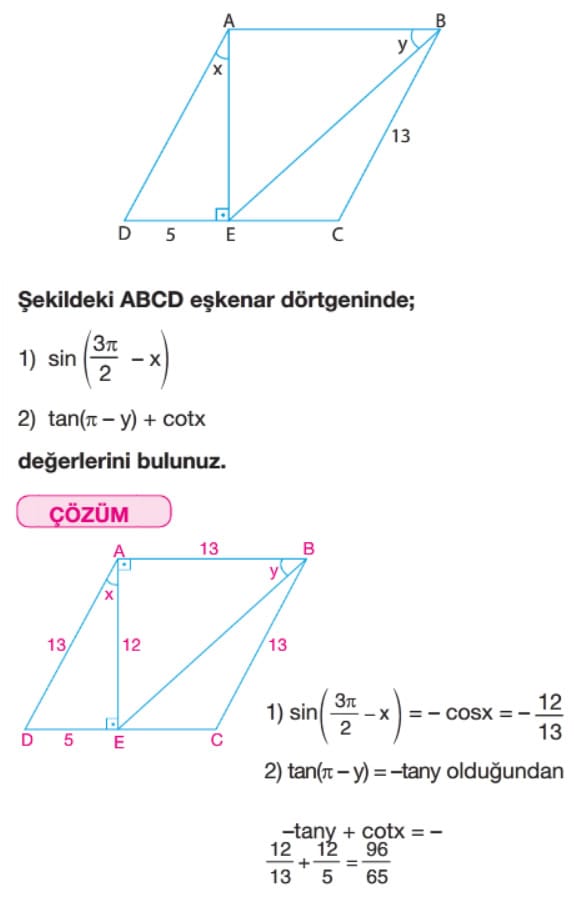
Çözüm: x bir dar açı olduğundan bir dik üçgen çizip içine x açısını yerleştirip verilen trigonometrik orana göre kenar oranları yazılabilir. Bilinmeyen kenar bu oranlara bağlı olarak bulunabilir.
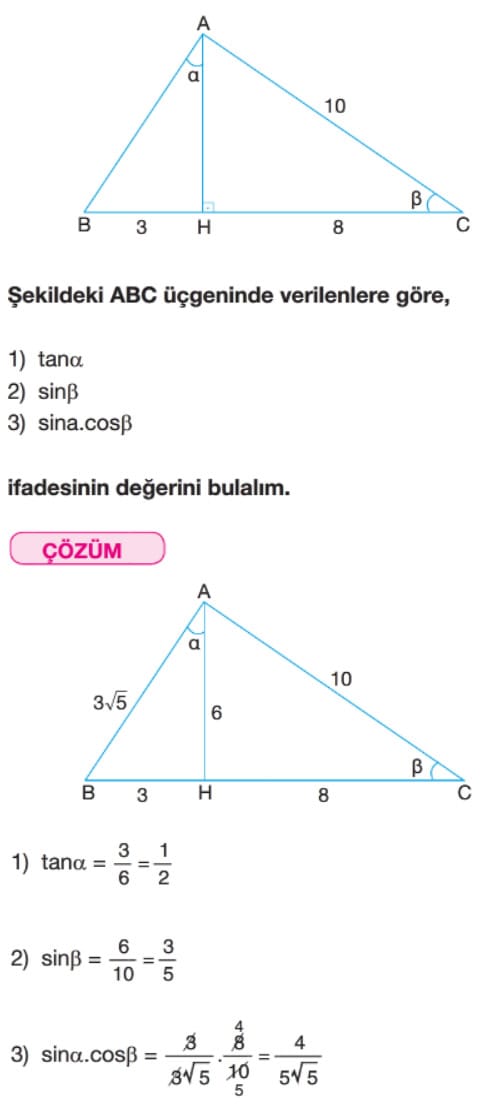
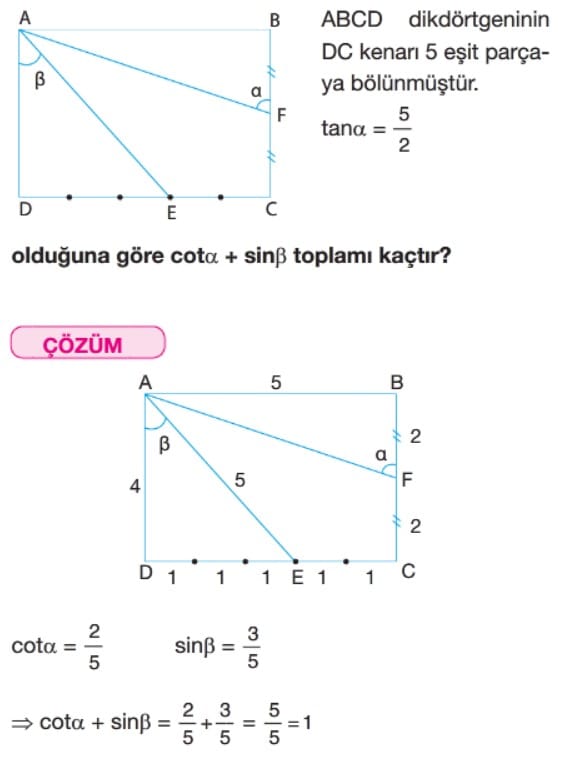
Çözüm: A açısına ait bir trigonometrik oran verildiği için dar açılardan biri  açısı olan bir dik üçgen oluşturmak üzere C köşesinde [AB] kenarına bir dik çizgi çizelim. Oluşan üçgenlerden birind nın verilen trigonometrik oranını kullanarak kenarları oranlayıp diğerinde â nin sorulan trigonometrik oranını bulabileceğiz.
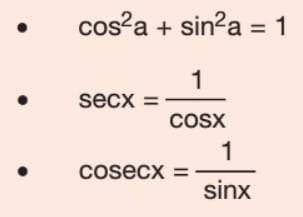

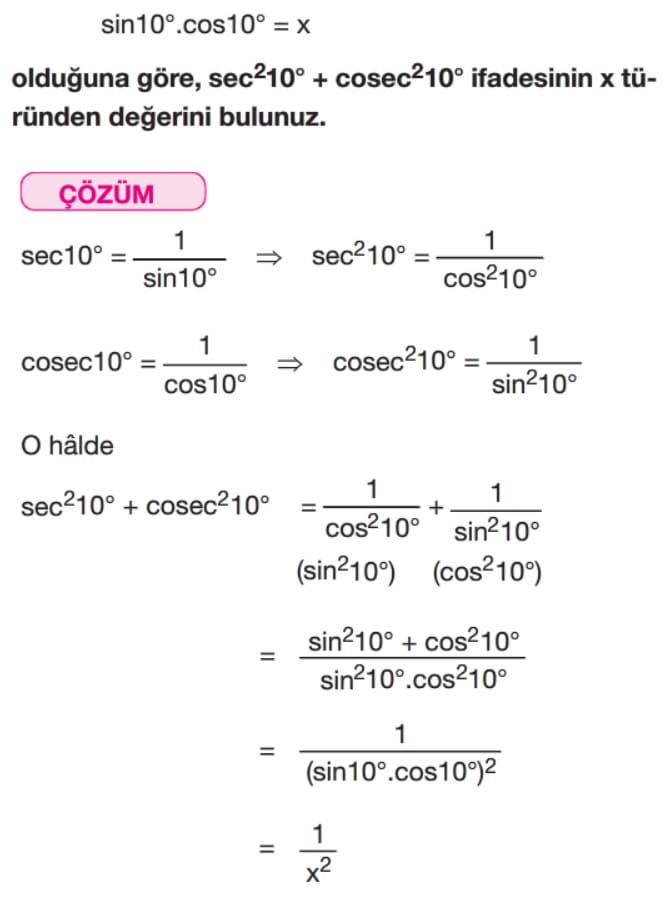
































İYİ GÜNLER