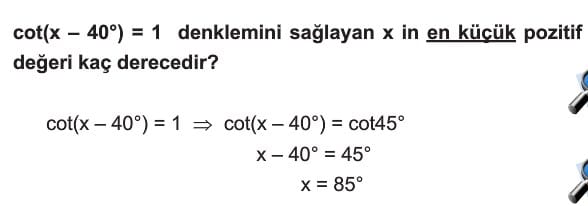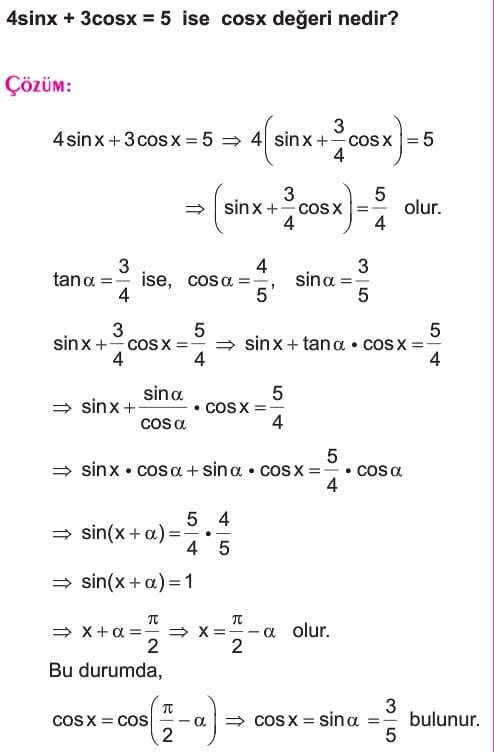Trigonometrik Denklemler 12. Sınıf
sinx = a denklemi
cosx = a denklemi
tanx = a denklemi
cotx = a denklemi
cosx ve sinx e Göre Lineer Denklemler
a, b, c sıfırdan farklı reel sayılar olmak üzere,
acosx + bsinx = c biçiminde ifade edilen denklemlere, cosx ve sinx e göre, lineer denklemler denir. Bu şekildeki denklemlerin çözülebilmesi için,
a2 + b2 ≥ c2 olmalıdır.
acosx + bsinx = c
denklemi çözülürken, her terim a ya (veya b ye) bölünür.
Denklemde oluşan terimlerden a/b ye (veya b/a ya) tanα denilerek denklem çözülür.
cosx ve sinx e Göre Homojen Denklemler
a ve b sıfırdan farklı reel sayılar olmak üzere,
acosx + bsinx = 0 biçiminde ifade edilen denklemlere homojen denklemler denir. bu denklemler, lineer denklemler gibi çözülebildiği gibi daha kolay yoldan da çözülebilir.
acosx + bsinx = 0 denkleminin her terimi cosx ≠ 0 ile bölünürse,
a+b.sinxcosx=0⇒a+b.tanx=0ise tanx=-ab
biçiminde elde edilen denklem ile çözülebilir.
cosx ve sinx e Göre İkinci Dereceden Homojen Denklemler
a, b, c den en az ikisi sıfırdan farklı reel sayılar olmak üzere;
a.cos2x + b.cosx.sinx + c.sin2x = 0
biçiminde ifade edilen denklemlere ikinci dereceden homojen denklemler denir.
a.cos2x + b.cosx.sinx + c.sin2x = 0 denklemini çözmek için, denklemin her terimi cos2x ≠ 0 ile bölünürse, bu denklem
a+bsinxcosx+csin2xcos2x=0a+b.tanx+c.tan2x=0
biçimine dönüşür.
Fonksiyonun En Büyük ve En Küçük Değeri
f(x) = a.sinx + b.cosx veya f(x) = a.sinx – b.cosx fonksiyonunun
En küçük değeri;-a2+b2En büyük değeri;a2+b2
olur.
Trigonometrik Denklemler Rehber Matematik
Trigonometrik Denklemler 1 Benim Hocam
Trigonometrik Denklemler 2 Benim Hocam
Çözümlü Örnek Test Soruları
Soru 1:
sin x = 1/2 denkleminin [0, 2π] aralığındaki çözümleri nelerdir?
A) x = π/6, 5π/6
B) x = π/4, 3π/4
C) x = π/3, 4π/3
D) x = π/2, 3π/2
Çözüm: sin x = 1/2 denkleminin [0, 2π] aralığındaki çözümleri x = π/6 ve x = 5π/6 değerleridir.
Cevap: A
Soru 2:
cos x = 1 denkleminin [0, 2π] aralığındaki çözümü nedir?
A) x = π
B) x = π/2
C) x = 0
D) x = 2π
Çözüm: cos x = 1 olduğu durumlarda x = 0 ve x = 2π olur.
Cevap: D
Soru 3:
tan x = √3 denkleminin [0, 2π] aralığındaki çözümleri nelerdir?
A) x = π/6, 5π/6
B) x = π/3, 4π/3
C) x = π/4, 3π/4
D) x = π/2, 3π/2
Çözüm: tan x = √3 denklemi için x = π/3 ve x = 4π/3 çözümleri elde edilir.
Cevap: B
Soru 4:
cot x = 1 denkleminin [0, 2π] aralığındaki çözümleri nelerdir?
A) x = π/4, 5π/4
B) x = π/3, 4π/3
C) x = π/2, 3π/2
D) x = 0, π
Çözüm: cot x = 1 olduğu durumlarda x = π/4 ve x = 5π/4 olur.
Cevap: A
Soru 5:
2 sin x = 1 denkleminin [0, 2π] aralığındaki çözümleri nelerdir?
A) x = π/6, 5π/6
B) x = π/4, 3π/4
C) x = π/3, 4π/3
D) x = π/2, 3π/2
Çözüm: 2 sin x = 1 ifadesi sin x = 1/2 olarak sadeleştirilebilir. Bu durumda x = π/6 ve x = 5π/6 olur.
Cevap: A
Soru 6:
cos x = -1/2 denkleminin [0, 2π] aralığındaki çözümleri nelerdir?
A) x = 2π/3, 4π/3
B) x = π/3, 5π/3
C) x = π/4, 3π/4
D) x = π/2, 3π/2
Çözüm: cos x = -1/2 olduğunda x = 2π/3 ve x = 4π/3 olur.
Cevap: A
Soru 7:
sin x = -1 denkleminin [0, 2π] aralığındaki çözümü nedir?
A) x = π
B) x = 3π/2
C) x = π/2
D) x = 2π
Çözüm: sin x = -1 olduğunda x = 3π/2 olur.
Cevap: B
Soru 8:
tan x = 0 denkleminin [0, 2π] aralığındaki çözümleri nelerdir?
A) x = π/2, 3π/2
B) x = π, 2π
C) x = 0, π
D) x = 0, 2π
Çözüm: tan x = 0 olduğunda x = 0 ve x = π değerlerini alır.
Cevap: C
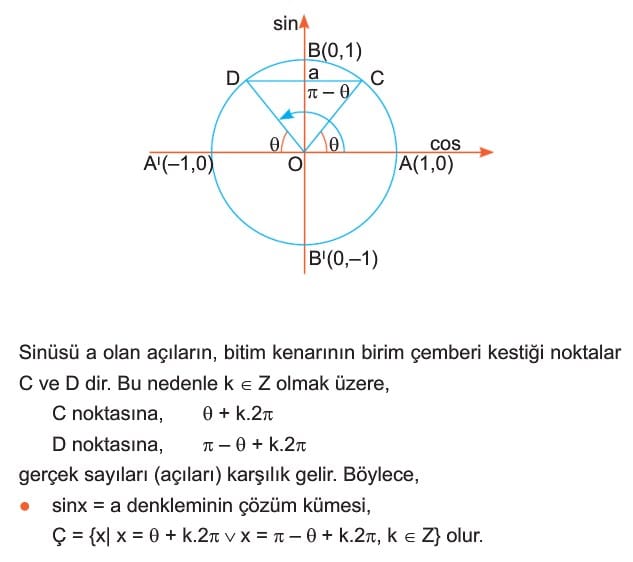
sinx = a denklemi: sinüsü a olan açıların, bitim kenarının birim çemberi kestiği noktalar C ve D dir. Bu nedenle k bir tam sayı olmak üzere, C noktasına, teta + 2.k.pi ve D noktasına, Pi – teta + 2kpi gerçek sayıları (açıları) karşılık gelir. Böylece sinx = a denkleminin çözüm kümesi
Ç = {x| x = teta +2.k.pi veya x = pi – teta + 2.k.pi, k bir tam sayı } olur.
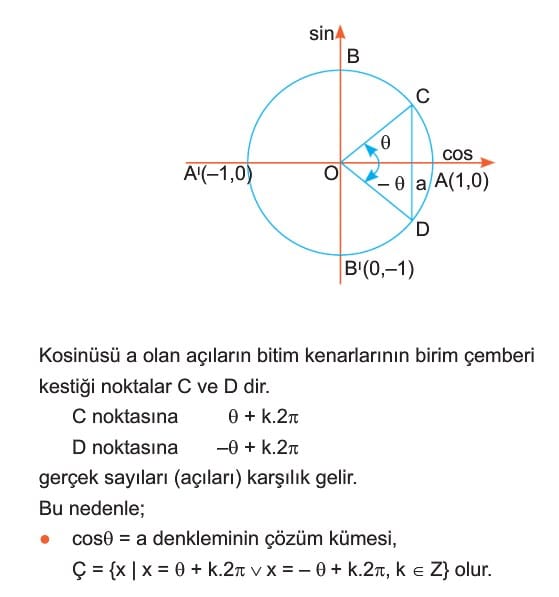
cosx = a denklemi: Kosinüsü a olan açıların, bitim kenarının birim çemberi kestiği noktalar C ve D dir. C noktasına, teta + 2.k.pi ve D noktasına, -teta + 2kpi gerçek sayıları (açıları) karşılık gelir. Bu nedenle;
cosx = a denkleminin çözüm kümesi,
Ç = {x| x = teta + 2.k.pi veya x = – teta + 2.k.pi, k bir tam sayı } olur.
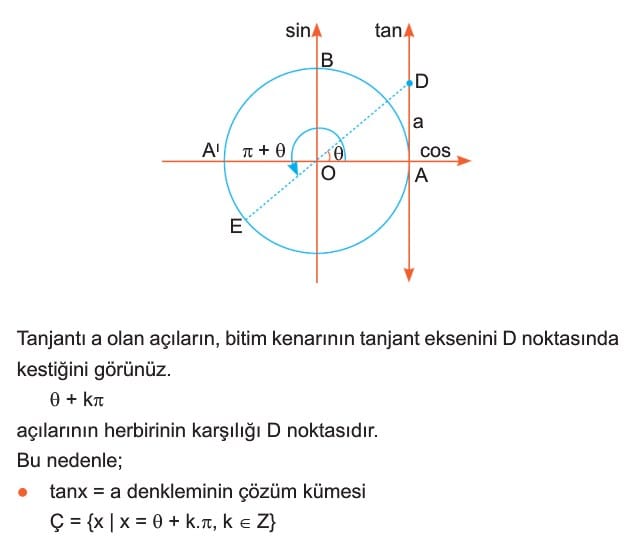
tanx= a denklemi: tanjantı a olan açıların, bitim kenarının tanjant eksenini D noktasında kestiğini görürüz. teta + k.pi açılarının herbirinin karşılığı d noktasıdır. Bu nedenle;
tanx = a denkleminin çözüm kümesi,
Ç = {x| x = teta + k.pi, k bir tam sayı } olur.
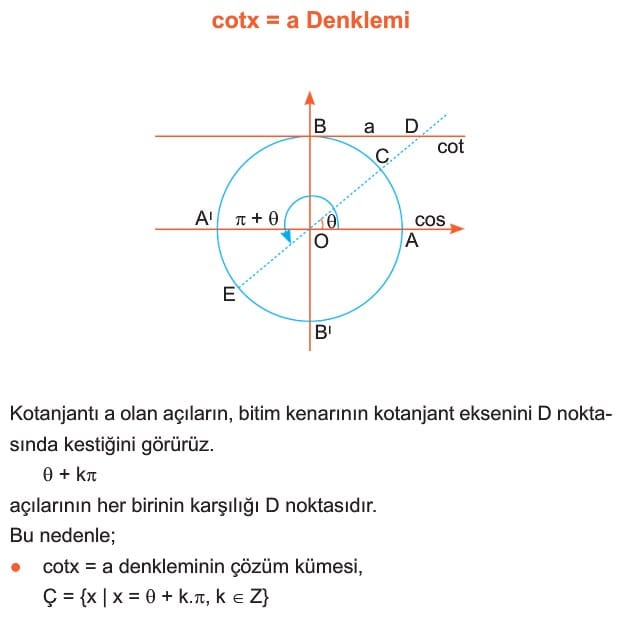
cotx = a denklemi: kotanjantı a olan açıların, bitim kenarının kotanjant eksenini D noktasında kestiğini görürüz. teta + k.pi açılarının herbirinin karşılığı D noktasıdır. Bu nedenle;
cotx = a denkleminin çözüm kümesi,
Ç = {x| x = teta + k.pi, k bir tam sayı } olur.