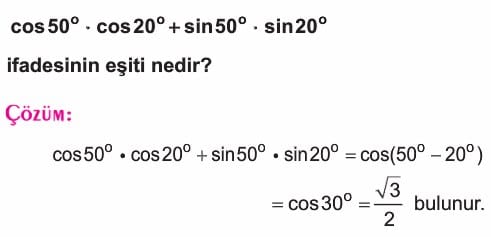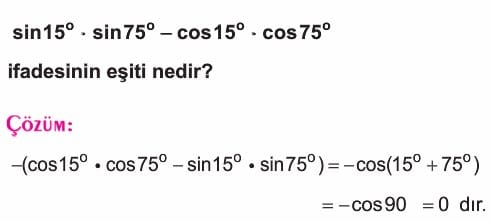İki açının toplamının sinüsü, kosinüsü, tanjantı ve kotanjantı

Toplam ve Fark Formülleri Soruları ve Çözümleri

Çözümlü Örnek Test Soruları

1. Sin(75°) toplam fark formüllerinden hangisi ile ifade edilebilir?
A) Sin(45° + 30°)
B) Cos(45° + 30°)
C) Tan(45° – 30°)
D) Cos(45° – 30°)
Çözüm:
Sin(75°), toplam fark formülüne göre Sin(a + b) = Sin a × Cos b + Cos a × Sin b olarak ifade edilir. Burada a = 45° ve b = 30° seçildiğinde, Sin(75°) = Sin(45° + 30°) olur.
Doğru cevap: A

2. Cos(15°) toplam fark formüllerinden hangisi ile ifade edilebilir?
A) Cos(45° – 30°)
B) Sin(45° + 30°)
C) Tan(45° – 30°)
D) Cos(30° – 15°)
Çözüm:
Cos(15°), fark formülüne göre Cos(a – b) = Cos a × Cos b + Sin a × Sin b olarak ifade edilir. Burada a = 45° ve b = 30° seçildiğinde, Cos(15°) = Cos(45° – 30°) olur.
Doğru cevap: A

3. Sin(105°) ifadesi toplam fark formülleri kullanılarak aşağıdaki ifadelerden hangisine eşittir?
A) Sin(60° + 45°)
B) Cos(45° + 30°)
C) Tan(60° + 30°)
D) Sin(90° + 15°)
Çözüm:
Sin(105°), toplam fark formülüne göre Sin(a + b) = Sin a × Cos b + Cos a × Sin b olarak ifade edilir. Burada a = 60° ve b = 45° seçildiğinde, Sin(105°) = Sin(60° + 45°) olur.
Doğru cevap: A

4. Tan(75°) toplam fark formülleri kullanılarak aşağıdaki ifadelerden hangisine eşittir?
A) Tan(45° + 30°)
B) Sin(45° + 30°)
C) Cos(45° – 30°)
D) Tan(60° + 15°)
Çözüm:
Tan(75°), toplam fark formülüne göre Tan(a + b) = (Tan a + Tan b) / (1 – Tan a × Tan b) olarak ifade edilir. Burada a = 45° ve b = 30° seçildiğinde, Tan(75°) = Tan(45° + 30°) olur.
Doğru cevap: A

5. Cos(75°) toplam fark formülleri ile aşağıdaki ifadelerden hangisine eşittir?
A) Cos(45° + 30°)
B) Sin(45° + 30°)
C) Tan(60° – 15°)
D) Sin(30° + 45°)
Çözüm:
Cos(75°), toplam fark formülüne göre Cos(a + b) = Cos a × Cos b – Sin a × Sin b olarak ifade edilir. Burada a = 45° ve b = 30° seçildiğinde, Cos(75°) = Cos(45° + 30°) olur.
Doğru cevap: A

6. Sin(135°) toplam fark formülleri ile aşağıdaki ifadelerden hangisine eşittir?
A) Sin(90° + 45°)
B) Cos(90° + 45°)
C) Sin(180° – 45°)
D) Tan(90° – 45°)
Çözüm:
Sin(135°), toplam fark formülüne göre Sin(a + b) = Sin a × Cos b + Cos a × Sin b olarak ifade edilir. 135° = 180° – 45° olduğundan, Sin(135°) = Sin(180° – 45°) olur.
Doğru cevap: C

Örnek: sinüs yirmi derece . kosinüs kırk derece + sinüs kırk derece . kosinüs 20 derece işleminin sonucunu bulunuz.
Çözüm: Verilen ifade 20 ve 40 derecenin sinüs toplam formülünün açılımıdır. Dolayısıyla sonuç sinüs 20+40 dan sinüs 60 dereceye eşittir. sinüs 60 derece de 30-60-90 üçgeninin çizerseniz karşı bölü hipotenüs formülünden kök 3 bölü 2 bulunur.

Örnek: Arktanjant bir bölü üç + arkkotanjant iki ifadesinin eşitini bulunuz.
Çözüm: arktanjant bir bölü üç eşittir x dersek tanjant x eşittir 1 bölü 3 olur. arkkotanjant iki eşittir y ise tanjant y eşittir 2 olur. arktanjant bir bölü üç + arkkotanjant iki eşittir a diyelim. buradan tan(arktanjant 1 bölü 3 + arkkotanjant 2) eşittir tanjant a olur. Verilen değerler yerine yazılırsa tanjant x + y eşittir tanjant a ise tanjantın toplam formülünden (1 bölü 3 + 1 bölü 2) bölü 1 – 1 bölü 3 . 1 bölü 2 eşittir 1 olur. tanjantı 1 olan açı pi bölü 4 dür.

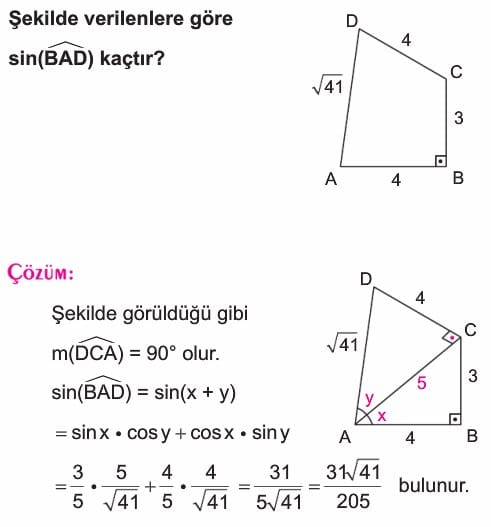
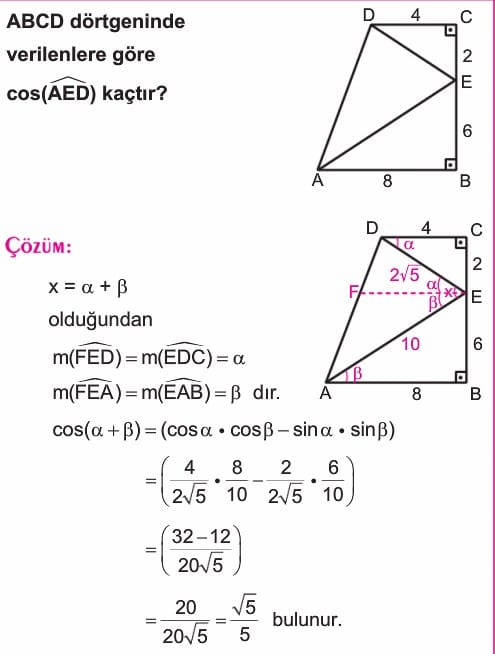
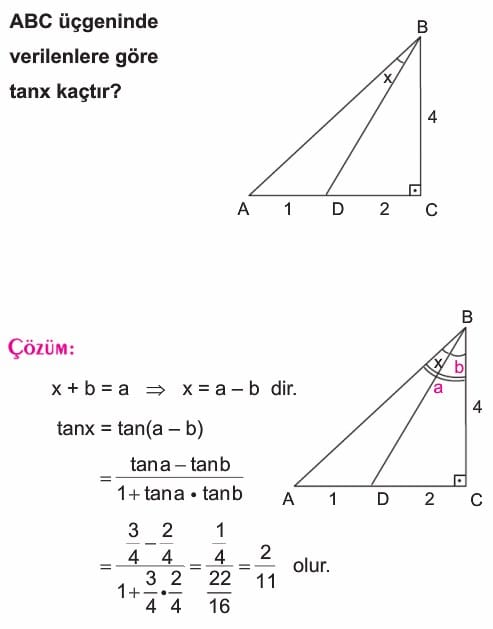
Örnek: Şekilde BCA açısı dik olan ACB üçgeni ve üçgenin B köşesinden karşı AC kenarına çizilen BD doğru parçası verilmiştir. AD eşittir 1, DC uzunluğu eşittir 2, BC uzunluğu eşittir 4 ve ABD açısı x olmak üzere tanjant x değerini bulunuz.
Çözüm: ABC açısına a ve DBC açısına b dersek x eşittir a – b olur. Buradan tanjant x eşittir tanjant a – b bulunur. Tanjantın fark formülü uygulanırsa tanjant x 2 bölü 11 olarak bulunur.