Arcsin Fonksiyonu

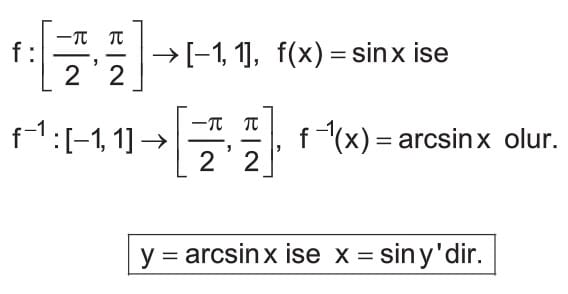
Arccos Fonksiyonu

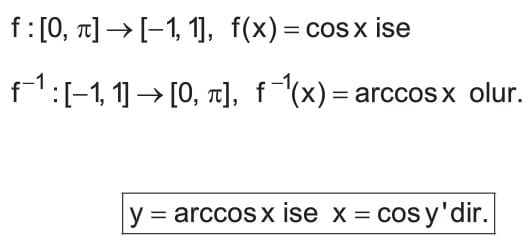
Arctan Fonksiyonu

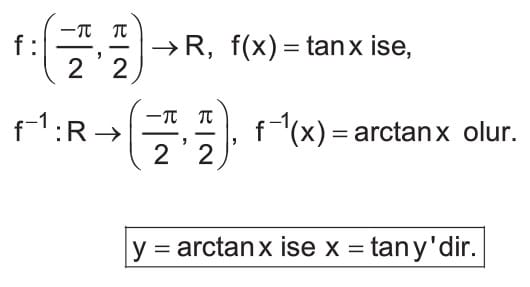
Arccot Fonksiyonu

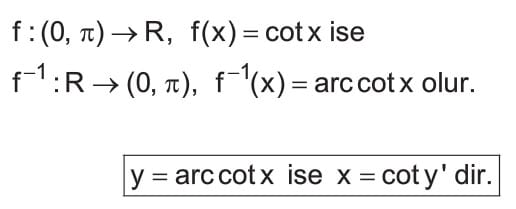
Ters Trigonometrik Fonksiyonlar Çözümlü Sorular

Çözümlü Örnek Test Soruları: Ters Trigonometrik Fonksiyonlar

Soru 1
arcsin(0.5) ifadesinin değeri kaçtır?
A) π/6
B) π/4
C) π/3
D) π/2

Çözüm
arcsin(0.5) ifadesi, sinüs değeri 0.5 olan açıyı temsil eder. Bu açı π/6’dır.
Doğru cevap: A

Soru 2
arccos(-1) ifadesinin değeri kaçtır?
A) 0
B) π/2
C) π
D) 2π

Çözüm
arccos(-1), kosinüs değeri -1 olan açıyı ifade eder. Bu açı π’dir.
Doğru cevap: C

Soru 3
arctan(1) ifadesinin değeri nedir?
A) 0
B) π/4
C) π/3
D) π/2

Çözüm
arctan(1), tanjant değeri 1 olan açıyı ifade eder. Bu açı π/4’tür.
Doğru cevap: B

Soru 4
arcsin(-√3/2) ifadesinin değeri nedir?
A) -π/3
B) -π/4
C) -π/6
D) π/3

Çözüm
arcsin(-√3/2), sinüs değeri -√3/2 olan açı -π/3’tür.
Doğru cevap: A

Soru 5
arccos(1/2) ifadesinin değeri nedir?
A) π/6
B) π/4
C) π/3
D) π/2

Çözüm
arccos(1/2), kosinüs değeri 1/2 olan açı π/3’tür.
Doğru cevap: C

Soru 6
arctan(-√3) ifadesinin değeri nedir?
A) -π/3
B) -π/4
C) -π/6
D) π/3

Çözüm
arctan(-√3), tanjant değeri -√3 olan açı -π/3’tür.
Doğru cevap: A

Soru 7
Eğer arcsin(x) = π/4 ise, x kaçtır?
A) √2/2
B) √3/2
C) 1/2
D) 0

Çözüm
arcsin(x) = π/4 ifadesi, sinüsün π/4 açısındaki değerine eşittir. Bu değer √2/2’dir.
Doğru cevap: A

Soru 8
Eğer arccos(x) = π/6 ise, x kaçtır?
A) 1/2
B) √3/2
C) √3
D) -√3/2

Çözüm
arccos(x) = π/6 ifadesi, kosinüsün π/6 açısındaki değerine eşittir. Bu değer √3/2’dir.
Doğru cevap: B

Arcsin: f fonksiyonu eksi pi bölü iki virgül pi bölü iki den eksi bir virgül bir kapalı aralığına tanımlı f(x) eşittir sinx fonksiyonu birebir ve örten bir fonksiyon olduğundan f üzeri eksi bir fonksiyonuna sinx fonksiyonunun ters fonksiyonu denir. sinx in ters fonksiyonu arcsinx  ile gösterilir.
Arccos: f fonksiyonu sıfır virgül pi den eksi bir virgül bir kapalı aralığına tanımlı f(x) eşittir cos x fonksiyonu birebir ve örten bir fonksiyon olduğundan f üzeri eksi bir fonksiyonuna cosx fonksiyonunun ters fonksiyonu denir. cosx in ters fonksiyonu arccosx  ile gösterilir.
Örnek: arcsin bir bölü iki nin değerini bulalım.
Çözüm: arcsin bir bölü iki eşittir x ise elemanların yerini değiştirirsek sinx eşittir bir bölü iki bulunur. sinüs değeri bir bölü iki olan eksi pi bölü ile pi bölü iki arasında olan açı pi bölü 6 yani 30 derecedir.
Örnek:  tan (90 + arcsin iki bölü kök beş ifadesinin değerini bulalım.
Çözüm: arcsin iki bölü kök beş eşittir alfa dersek tanjant doksan artı alfa eksi kotanjant alfaya eşit olur. Buradan alfa açısına özel dik üçgen çizersek pisagor teoreminden kenarlar bir, iki ve kök beş bulunur. Buradan eksi kotanjant alfa eksi bir bölü iki bulunur.
Arctan: f eksi pi bölü 2 virgül pi bölü iki açık aralığından gerçek sayılara tanımlı bir fonksiyondur. Bu f(x) eşittir tanjant x fonksiyonu birebir ve örtendir. R den eksi pi bölü 2 virgül pi bölü iki açık aralığına tanımlı f fonksiyonuna tanjant fonksiyonunun ters trigonometrik fonksiyonu denir ve arctanx ile gösterilir.