Temel Orantı Teoremi 9. Sınıf Matematik (Yeni Müfredat) Ders Notu
Temel Orantı Teoremi, bir üçgende paralel doğrular ve bu doğruların kesiştiği kenarlar arasında oluşan oranları inceleyen önemli bir geometrik kuraldır. Bu teorem, paralel doğruların oluşturduğu parçaların oranlarının eşit olduğunu ifade eder ve bu sayede benzerlik, oran ve orantı kavramlarının anlaşılmasını sağlar. Günlük hayatta harita ölçeklendirme, mimari tasarım ve mühendislik projelerinde sıkça kullanılan bu teorem, üçgenlerde orantılılık kurallarını anlamayı kolaylaştırır. Yeni nesil matematik soruları, bu teoremi gerçek hayattan alınan hikayelerle ilişkilendirerek öğrencilerin analitik düşünme becerilerini geliştirmeyi amaçlamaktadır.
Tales, Öklid ve Pisagor Teoremleri Testleri
Temel Orantı Teoremi Ders Notu (Yeni Müfredat)
Bir üçgenin bir kenarına paralel olan ve diğer iki kenarını kesen bir doğru, kestiği kenarları orantılı parçalara ayırır. Bu teoreme temel orantı teoremi denir.
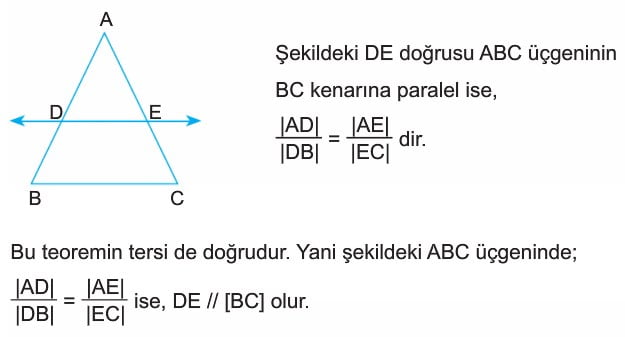
Örnek:
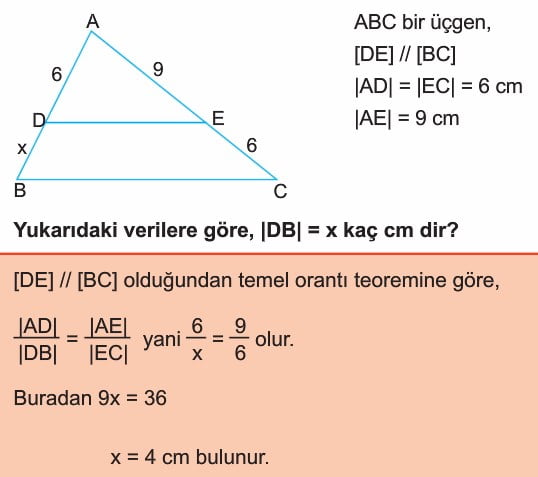
Örnek:
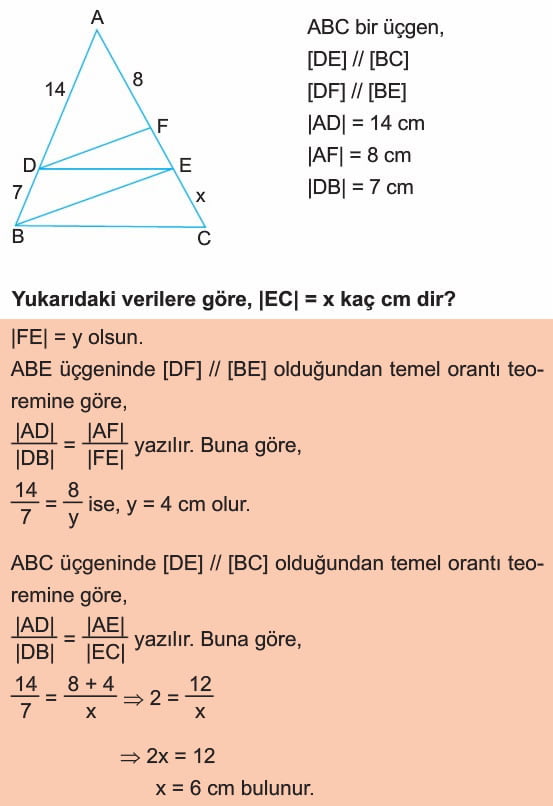
Çözümlü Örnek Test Soruları
1. Soru
Bir üçgenin bir kenarı 8 cm uzunluğundadır ve paralel doğrular bu kenarı 3 cm ve 5 cm uzunluklarında iki parçaya ayırmıştır. Diğer kenarda bu doğrulara karşılık gelen parçalar sırasıyla 6 cm ve x cm’dir. x kaçtır?
a) 7
b) 8
c) 9
d) 10
e) 12
Çözüm:
Orantı denklemi:
3 × x = 5 × 6
3x = 30
x = 30 ÷ 3
x = 10
Cevap: d) 10
2. Soru
Bir üçgende bir kenar 12 cm uzunluğundadır ve paralel doğrular bu kenarı 4 cm ve 8 cm olarak iki parçaya bölmüştür. Diğer kenarın parçaları 6 cm ve x cm ise x kaçtır?
a) 10
b) 11
c) 12
d) 13
e) 14
Çözüm:
Orantı denklemi:
4 × x = 8 × 6
4x = 48
x = 48 ÷ 4
x = 12
Cevap: c) 12
3. Soru
Bir üçgende bir kenar 15 cm uzunluğundadır ve paralel doğrular bu kenarı 5 cm ve 10 cm olarak iki parçaya ayırmıştır. Diğer kenarın parçaları 9 cm ve x cm ise x kaçtır?
a) 15
b) 16
c) 17
d) 18
e) 20
Çözüm:
Orantı denklemi:
5 × x = 10 × 9
5x = 90
x = 90 ÷ 5
x = 18
Cevap: d) 18
4. Soru
Bir üçgenin bir kenarı 20 cm uzunluğundadır ve paralel doğrular bu kenarı 8 cm ve 12 cm olarak iki parçaya ayırmıştır. Diğer kenarın parçaları 10 cm ve x cm ise x kaçtır?
a) 12
b) 14
c) 15
d) 16
e) 18
Çözüm:
Orantı denklemi:
8 × x = 12 × 10
8x = 120
x = 120 ÷ 8
x = 15
Cevap: c) 15
5. Soru
Bir üçgenin bir kenarının uzunluğu 9 cm’dir ve paralel doğrular bu kenarı 3 cm ve 6 cm olarak iki parçaya bölmüştür. Diğer kenarın parçaları 4 cm ve x cm ise x kaçtır?
a) 6
b) 8
c) 9
d) 10
e) 12
Çözüm:
Orantı denklemi:
3 × x = 6 × 4
3x = 24
x = 24 ÷ 3
x = 8
Cevap: b) 8
6. Soru
Bir üçgende bir kenarın uzunluğu 24 cm’dir ve paralel doğrular bu kenarı 6 cm ve 18 cm olarak iki parçaya ayırmıştır. Diğer kenarın parçaları 8 cm ve x cm ise x kaçtır?
a) 20
b) 21
c) 22
d) 24
e) 25
Çözüm:
Orantı denklemi:
6 × x = 18 × 8
6x = 144
x = 144 ÷ 6
x = 24
Cevap: d) 24
7. Soru
Bir üçgenin bir kenarının uzunluğu 30 cm’dir ve paralel doğrular bu kenarı 10 cm ve 20 cm olarak iki parçaya ayırmıştır. Diğer kenarın parçaları 12 cm ve x cm ise x kaçtır?
a) 20
b) 24
c) 26
d) 30
e) 36
Çözüm:
Orantı denklemi:
10 × x = 20 × 12
10x = 240
x = 240 ÷ 10
x = 24
Cevap: b) 24
8. Soru
Bir üçgende paralel doğruların oluşturduğu parçalar 7 cm ve 14 cm’dir. Bu doğruların diğer kenarda oluşturduğu parçalar 10 cm ve x cm ise x kaçtır?
a) 18
b) 19
c) 20
d) 21
e) 22
Çözüm:
Orantı denklemi:
7 × x = 14 × 10
7x = 140
x = 140 ÷ 7
x = 20
Cevap: c) 20
9. Soru
Bir üçgenin kenar uzunlukları 12 cm ve 18 cm’dir. Paralel doğrular bu kenarlarda sırasıyla 4 cm ve x cm uzunluğunda parçalar oluşturmuştur. x kaçtır?
a) 5
b) 6
c) 7
d) 8
e) 9
Çözüm:
Orantı denklemi:
4 × 18 = 12 × x
72 = 12x
x = 72 ÷ 12
x = 6
Cevap: b) 6





