Temel kavramlar Tyt
Matematikte en temel iki kavram rakam ve sayıdır. Bu iki kavram, öğreneceğimiz tüm bilgi ve formüller için bir bakıma yapı taşı niteliğindedir. Rakam ve sayıyı öğrendikten sonra her biri birer küme olan sayıların sınıflandırılmasını öğreneceğiz. Sayıları; sayma sayıları, doğal sayılar, tam sayılar, rasyonel sayılar, irrasyonel sayılar ve reel (gerçel) sayılar şeklinde sınıflandıracağız.
RAKAM VE SAYI
Sayıları ifade etmek için kullanılan sembollere rakam denir. {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} kümesinin elemanları onluk sayma sisteminde birer rakamdır.
- Onluk sayma sisteminde en küçük rakam 0, en büyük rakam 9 dur.
- Rakamların bir araya getirilmesiyle oluşturulan ifadelere sayı denir.
Bilgi: Her rakam sayıdır, fakat her sayı rakam değildir.
Örnek:
- 0, hem bir rakam hem de bir sayıdır.
- 5, hem bir rakam hem de bir sayıdır.
- 13, bir sayıdır, fakat onluk sayma sisteminde bir rakam değildir.
- 346, bir sayıdır.
Örnek: a ve b birer rakam olmak üzere,
a + b = 7
olduğuna göre, a – b farkı en çok kaçtır?
A) 1 B) 2 C) 4 D) 7 E) 8
Çözüm: a – b farkı en çok olacağına göre, a en büyük ve b en küçük değerini almalıdır.
a + b = 7 toplamında;
a nın en büyük değeri 7, b nin en küçük değeri 0 dır.
Buna göre, a – b = 7 – 0 = 7 olur.
Cevap D
Örnek: a, b ve c sıfırdan farklı birer rakam olmak üzere,
a = 2b ve b = 3c
olduğuna göre, a + b + c toplamı kaçtır?
Çözüm: a, b ve c sıfırdan farklı birer rakamdır.
c = 3 ise b = 9 ve a = 18 olur. Bu durumda, a rakam olmaz.
c = 2 ise b = 6 ve a = 12 dir. Bu durumda, a yine rakam olmaz.
c = 1 ise b = 3 ve a = 6 dır.
Öyleyse, a + b + c = 6 + 3 + 1 = 10 olur.
SAYILARIN SINIFLANDIRILMASI
Sayıları; sayma sayıları, doğal sayılar, tam sayılar, rasyonel sayılar, irrasyonel sayılar ve reel (gerçel) sayılar olarak sınıflara ayırabiliriz.
Sayma Sayıları
Nesnelerin adedini saymak için kullandığımız sayılara sayma sayıları denir. Sayma sayıları kümesi N+ ile gösterilir.
N+ = (1, 2, 3, 4, …} kümesinin elemanları sayma sayılarıdır.
Doğal Sayılar
{0, 1, 2, 3, 4, …} kümesine doğal sayılar kümesi denir ve N ile gösterilir.
N = {0, 1, 2, 3, 4, …} kümesinin her bir elemanına doğal sayı denir.
Bilgi: Doğal sayılar kümesinin en küçük elemanı 0 dır. Doğal sayılar kümesinin en büyük elemanı bilinemez.
Tam Sayılar
Doğal sayılar kümesine 0 dan farklı doğal sayıların negatiflerinin eklenmesi ile elde edilen küme tam sayılar kümesidir.
Z = {…, -3, -2, -1, 0, 1, 2, 3, …} kümesi tam sayılar kümesidir ve bu kümesinin her bir elemanına tam sayı denir.
Pozitif Tam Sayılar, Negatif Tam Sayılar
Pozitif tam sayılar kümesi Z+ = {1, 2, 3, …} biçiminde gösterilir.
Negatif tam sayılar kümesi Z– = {…, -3, -2, -1) biçiminde gösterilir.
Tam sayılar kümesi
Z = Z+ ∪ {0} ∪ Z– şeklinde gösterilir. Öyleyse, tam sayılar kümesi, pozitif tam sayılar, negatif tam sayılar ve sıfırın birleşiminden oluşur.Bilgi: Soru çözümlerinde hangi sayı kümesinde işlem yapıldığını bilmek çok önemlidir. Bu durum genellikle sorunun başlangıcında ifade edilir. Örneğin; x, y ve z birer tam sayı olmak üzere, … gibi
Tam sayılar kümesinde işlem yaparken aşağıdaki bilgiler büyük önem taşır.
- En büyük negatif tam sayı -1 dir.
- En küçük pozitif tam sayı 1 dir.
- 0 (sıfır) hem doğal sayı hem de tam sayıdır.
- 0 (sıfır) pozitif veya negatif değildir. Yani, işaretsizdir.
Bilgi: Bir değişkenin diğer bir değişken türünden ifade edilebilmesi problem çözümlerinde kolaylık sağlar. Bir denklemde, değişkenin değerlerinin birer birer yazılıp diğerinin bulunması yorucu olabilir ve uzun süre alabilir.
Tam Sayılarda İşlemler
Tam Sayılarda İşlem Önceliği
Tam sayılarda dört işlemden bir kısmı birlikte verildiğinde öncelikli olarak aşağıdaki sıralamayı takip edebiliriz:
- Parantezler
- Çarpma ya da bölme
- Toplama ya da çıkarma
Rasyonel Sayılar
a ve b tam sayılar ve b ≠ 0 olmak üzere şeklinde yazılabilen sayılara rasyonel sayılar denir. Rasyonel sayılar kümesi Q ile gösterilir ve
biçiminde yazılır.
rasyonel sayısında a ya payi b ye payda denir.
İrrasyonel Sayılar
Reel (Gerçek) Sayılar
Örnek
I. Rasyonel sayılar kümesi ile irrasyonel sayılar kümesi ayrık kümelerdir.
II. İki irrasyonel sayının çarpımı bir irrasyonel sayıdır.
III. Bir pozitif ve bir negatif reel sayının toplamı pozitif olamaz.
IV. Her tam sayı bir rasyonel sayıdır.
ifadelerden kaç tanesi daima doğrudur?
A) 0 B) 1 C) 2 D) 3 E) 4
Çözüm: Ayrık kümelerin ortak elemanı yoktur.
I. ve IV. ifadeleri daima doğrudur.
II. ve III. ifadeleri doğru olmayabilir.
II. ifadenin yanlışlığı göstermek için = 2 alabiliriz.
III. ifadenin yanlışlığı göstermek için 7 + (-3) = 4 alabiliriz. Cevap C
Bilgi: Bir tam sayının karesi olan sayılara tam kare sayı denir.
Örneğin; 0, 1, 4, 9, 16, 25 birer tam karedir. (-3)2 = 32 = 9 dur.
Çift Sayı, Tek Sayı
2 ile tam bölünebilen tam sayılara çift sayılar, tam bölünemeyen tam sayılara tek sayılar denir.
Örnek
-6, -2, 0, 2, 4, 8, 12, 24, 102 birer çift sayı;
-9, -3, 1, 7, 11 ,45, 87 birer tek sayıdır.
- Tek sayı ve çift sayı sadece tam sayılarda geçerlidir.
- 0 çift sayıdır.
- Negatif sayılarda da tek sayı ya da çift sayı kavramı vardır.
Pozitif Sayı, Negatif Sayı
Ardışık Sayılar
Ardışık Sayıların Sonlu Toplamları
Asal Sayılar
1 ve kendisinden başka pozitif bölenleri olmayan 1 den büyük doğal sayıya asal sayı denir.
2 nin pozitif bölenleri 1 ve 2 olduğundan 2 asal sayıdır.
4 ün pozitif bölenleri 1, 2 ve 4 olduğundan 4 asal sayı değildir.
Asal sayılar kümesinin bazı elemanları aşağıda verilmiştir.
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103
- 1 asal sayı değildir. En küçük asal sayı 2 dir.
- Çift asal sayı sadece 2 dir. 2 dışındaki tüm asal sayılar tek sayıdır.
Sonraki Konu: BASAMAK KAVRAMI
TEMEL KAVRAMLAR SORULARI VE ÇÖZÜMLERİ
Benim Hocam: İlyas Güneş Temel Kavramlar 1
Benim Hocam: İlyas Güneş Temel Kavramlar 1
Şenol Hoca: Temel Kavramlar 1
Şenol Hoca: Temel Kavramlar 2
Temel kavramlar Konu Anlatımı Test Soruları Çözümleri Tyt Matematik
Örnek: x, y ve z pozitif tam sayılar olmak üzere,
x - y = 4
z = 6y
olduğuna göre, y nin alabileceği değer için x + y + z toplamı kaçtır?
A) 25 B) 26 C) 27 D) 29 E) 32
Çözüm: x, y ve z nin birer pozitif tam sayı olduğuna dikkat ediniz. z = 6y eşitliğinde y çok büyük değerler alabilir diye düşünülebilir.
Oysa, x - y = 4 olduğundan y en çok 4 tür.
y = 4 ise x = 1 ve z = 24 tür. Bu durumda, x + y + z = 1 + 4 + 24 = 29 dur. Cevap D
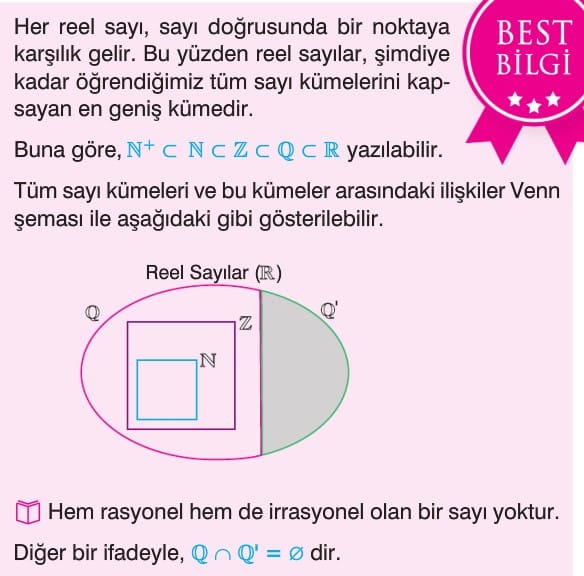
Bilgi: Her reel sayı, sayı doğrusunda bir noktaya karşılık gelir. Bu yüzden reel sayılar, şimdiye kadar öğrendiğimiz tüm sayı kümelerini kapsayan en geniş kümedir.
Her reel sayı, sayı doğrusunda bir noktaya karşılık gelir. Bu yüzden reel sayılar, şimdiye kadar öğrendiğimiz tüm sayı kümelerini kapsayan en geniş kümedir. Buna göre, N+ c N c Z c Q c R yazılabilir. Tüm sayı kümeleri ve bu kümeler arasındaki ilişkiler Venn şeması ile aşağıdaki gibi gösterilebilir.
Örnek: Bir sürücü kursuna kayıt yaptıran 80 öğrenciden her birine birer öğrenci numarası verilmiştir. Öğrenciler aşağıdaki bilgilere göre A ve B sınıflarına ayrılıyor. Numaralarındaki rakamların çarpımı; tek sayı olanlar A sınıfında ve çift sayı olanlar ise B sınıfındadır.
- B sınıfındaki öğrenci sayısı 52 dir.
- Numarasındaki rakamların an az biri tek sayı olan tam 68 öğrenci bulunmaktadır.
Buna göre, bu kursta numarasındaki rakamların biri tek diğeri çift sayı olan toplam öğrenci sayısı kaçtır?
A) 26 B) 23 C) 30 D) 32 E) 40
Çözüm: Tek sayıları (T) ile çift sayıları (Ç) ile gösterelim. İki tek sayısının çarpımı tek sayıdır. En az biri çift olan iki sayının çarpımı çift sayıdır. Buradan, numaralarındaki rakamların çarpımı T - Ç, Ç - T ve Ç - Ç biçiminde olan 52 öğrenci, T - Ç, Ç - T ve T - T biçiminde olan 68 öğrenci vardır. Öyleyse; Ç - Ç biçiminde olan 80 - 68 = 12 öğrenci vardır. Buna göre, T - Ç ve Ç - T biçiminde olan öğrenci sayısı 52 - 12 = 40 olur. Cevap E
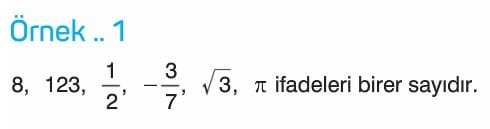







































































































Mükemmel 😍 tek kelimeyle bayıldım