Her bilim dalının kendine özgü anlamlar içeren sözcükleri dolayısıyla kendine özgü bir dili vardır. Bu dil, günlük yaşamımızda kullandığımız dilden ayrılır. Bu özel anlam içeren sözcüklere terim denir. Terim, tanımlı ve tanımsız terimler olmak üzere iki türlüdür. Biz bu kısımda matematik dilinin önemli kavramlarından tanım, aksiyon, teorem ve ispat kavramlarına değineceğiz.
Tanım: Bir terimi anlamları daha önceden bilinen terimler yardımıyla ifade etmeye tanım denir. İyi bir tanım, tanımlı ve tanımsız terimlerden yararlanmalı, herkes için açık, anlaşılır ve tutarlı olmalı, aynı türden kavramları kapsamalı, aynı türden olmayan kavramları dışarıda bırakmalıdır.
Örnek: Aşağıdaki terimlerin tanımlarını yapıp inceleyelim.
a. Işın b. Çember c. Rakam
Çözüm:
a. “Işın: Başlangıç noktası belli olan ve o noktadan sonsuza doğru uzanan noktalar kümesidir.” Bu tanımda geçen nokta, sonsuz ve küme kavramları yine birer terimdir.
b. “Çember: Düzlemde bir noktaya eşit uzaklıktaki noktalar kümesidir.” Burada da düzlem, nokta, eşitlik, uzaklık ve küme kavramları birer terimdir.
c. “Rakam: Sayıları ifade etmeye yarayan sembollere denir.” Bu tanımda geçen sayı, sembol yine birer terimdir.
Aksiyom: Mantık ve matematikte teorem ispatında öncül işlevi gören, doğruluğu açık ve seçik olarak belirli olan ve bu nedenle ispatına gerek duyulmayan önermelere aksiyom denir.
Örnek: Aşağıda aksiyom örnekleri verilmiştir. İnceleyiniz.
a. İki farklı noktadan yalnız bir doğru geçer.
b. Tüm dik açıların ölçüleri birbirine eşittir.
c. Aynı düzlemde kesişmeyen doğrular paraleldir.
ç. Bir doğal sayının ardışığı da doğal sayıdır.
Teorem: Doğruluğu ispatlanması gereken önermelere teorem denir. Bir teoremin verilen kısmına hipotez (varsayım), ispatlanacak olan kısmına hüküm (yargı) denir. Bir teoremin hipotezinden hareketle hükmünün doğru olduğunu göstermeye teoremi ispatlamak denir.
p ⇒ q, bir teorem ise p, teoremin hipotezi, q ise hükmüdür.
Örnek: “İki tek sayının çarpımı tek sayıdır.” teoreminin hipotez ve hükmünü belirtip ifade edelim.
Çözüm: Teoremler p⇒q biçiminde olmalıdır. O hâlde hipotez p: “a ve b tek sayıdır.”
Hüküm q: “a · b tek sayıdır.” olur. Buradan teorem p⇒q: ” a ve b tek sayı ise a · b tek sayıdır.”
şeklinde ifade edilir.
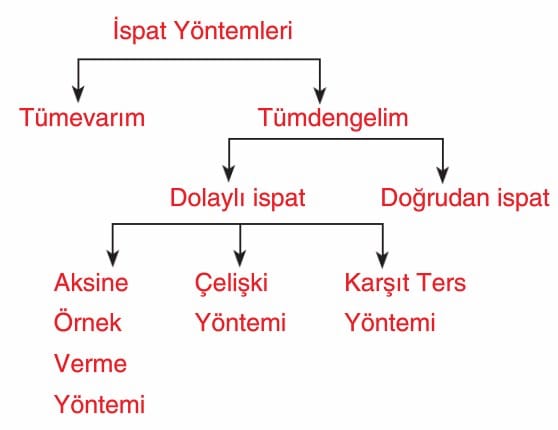
Tümevarım Yöntemi
p(n) açık önermesi için
1. adım: p(1) önermesinin doğru olduğu gösterilir.
2. adım: p(k) önermesinin doğru olduğu kabul edilir. (k ∈ N+)
3. adım: p(k + 1) önermesinin doğru olduğu gösterilir.
Doğrudan İspat Yöntemi: p ⇒ q teoreminde p nin doğru olduğu kabul edilerek q nun da doğru olduğu adım adım gösteriliyorsa buna doğrudan ispat yöntemi denir.
Olmayana Ergi Yöntemi (Karşıt Ters): Bir teoremin karşıt tersinin ispatlanması yöntemine olmayana ergi yöntemi denir.
Aksine Örnek Yöntemi: Önermenin doğru olmadığını gösteren en az bir değer bularak önermenin yanlış olduğunu ispatlamaya aksine örnek yöntemi
denir.
Çelişki Yöntemi: Bir teoremde hükmün olumsuzundan hareket edilerek çelişki elde etme yöntemine çelişki yöntemi denir.
teşekkurlr