Üslü sayılar, sayıların üst üste kaç kez çarpılacağını ifade eden önemli bir matematiksel kavramdır. Tam sayıların tam sayı kuvvetleri, bir sayının kendisiyle kaç kez çarpılacağını veya bölüneceğini ifade eder. Bu konu, LGS sınavında sıkça karşımıza çıkan bir konudur ve bu kavramı anlamak matematikte önemli beceriler kazandırır. Üslü sayılar, bilimsel gösterimler, hesaplamalar ve günlük hayatta sıkça kullanılır. Bu ders notunda, tam sayıların tam sayı kuvvetlerini öğrenirken örneklerle konuyu pekiştireceğiz.

Tam Sayıların Tam Sayı Kuvvetleri Testleri

Lgs 8. Sınıf Tam Sayıların Tam Sayı Kuvvetleri Konu Anlatımı

• Pozitif tam sayıların tüm kuvvetleri pozitiftir.
• Negatif tam sayıların çift kuvvetleri pozitif, tek kuvvetleri negatiftir.
• Çift kuvvet alınırken (-) işareti parantezin içinde ise sonuç pozitif, değilse negatiftir.
• a ve n birer tam sayı olmak üzere
  1ⁿ = 1, a¹ = a‘dır.

Tam Sayıların Negatif Tam Sayı Kuvvetleri

a ≠ 0 ve n bir doğal sayı olmak üzere,

Örnek Sorular

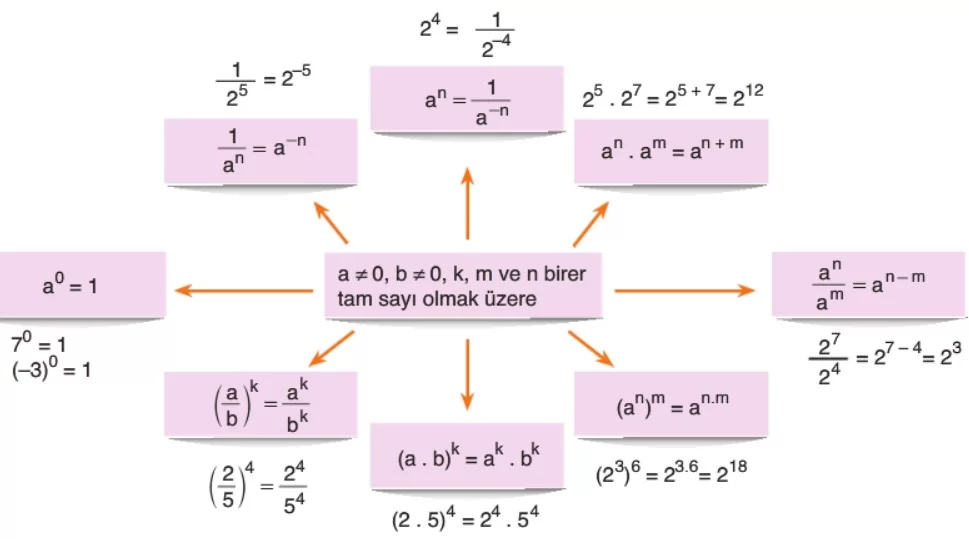
Üslü İfadelerle İlgili Temel Kurallar

Çözümlü Sorular

Örnek Çözümlü Sorular

Örnek 1:

Bir Bilim İnsanı ve Hücre Bölünmesi

Bir laboratuvarda çalışan bilim insanı, bir bakterinin her saatte ikiye bölündüğünü fark eder. Deney başladığında 1 bakteri olan ortamda, 6 saat sonunda kaç bakteri olacaktır?

Çözüm: Hücre her saat ikiye bölündüğü için her saatte bakteri sayısı iki katına çıkacaktır. Bu durumu üslü sayılarla ifade edebiliriz:

• Başlangıçta 1 bakteri var.
• 1. saat: 2⁰ × 2¹ = 2 bakteridir.
• 6 saat sonra: 2⁶ = 64

Sonuç olarak, 6 saat sonunda 64 bakteri olacaktır.

Sonuç: 6 saat sonunda 64 bakteri olur.

Örnek 2:

Robotların Üretimi

Bir teknoloji şirketi, her gün üretilen robot sayısını iki katına çıkararak bir deney yapmaktadır. İlk gün 5 robot üretilmişse, 4. günün sonunda toplam kaç robot üretilmiş olur?

Çözüm: Her gün üretilen robot sayısı iki katına çıkıyorsa, bu artışı üslü sayılarla ifade edebiliriz. İlk gün 5 robot üretilmişse:

• 1. gün: 5 robot
• 2. gün: 5 × 2¹ = 10 robot
• 3. gün: 5 × 2² = 20 robot
• 4. gün: 5 × 2³ = 40 robot

Toplam üretilen robot sayısı:

• 5 + 10 + 20 + 40 = 75 robot

Sonuç: 4 gün sonunda toplam 75 robot üretilmiştir.

Örnek 3:

Dünyanın En Hızlı Arabası

Bir araba yarışı düzenlenmiştir ve bu yarıştaki bir arabaya, her turda hızını iki katına çıkarma yeteneği verilmiştir. İlk turda hız 10 km/saattir. Üçüncü tur sonunda bu arabanın hızı kaç km/saattir?

Çözüm: Her turda araba hızını iki katına çıkarıyor, bu durumu üslü sayılarla ifade edebiliriz:

• 1. tur: 10 km/saat
• 2. tur: 10 × 2¹ = 20 km/saat
• 3. tur: 10 × 2² = 40 km/saat

Sonuç: Üçüncü tur sonunda arabanın hızı 40 km/saattir.

Örnek 4:

Mars’a Yolculuk

Bir uzay araştırma şirketi, her geçen gün Mars’a yaklaşan bir uzay aracını gözlemlemektedir. Aracın hızı her gün %50 azalıyor. İlk gün hızı 1000 km/saattir. 3 gün sonra aracın hızı kaç km/saate düşer?

Çözüm: Hız her gün yarı yarıya azaldığı için bu azalmayı negatif üslü sayılarla ifade edebiliriz:

• 1. gün: 1000 km/saat
• 2. gün: 1000 × (1/2) = 500 km/saat
• 3. gün: 1000 × (1/2)² = 250 km/saat

Sonuç: Üçüncü günün sonunda aracın hızı 250 km/saattir.

Örnek 5:

Bir Köyde Tavukların Çoğalması

Bir köyde her hafta tavuk sayısı 3 katına çıkmaktadır. İlk hafta 4 tavuk olan bu köyde, 3 hafta sonra kaç tavuk olur?

Çözüm: Her hafta tavuk sayısı 3 katına çıkıyorsa bu çoğalmayı üslü sayılarla ifade edebiliriz:

• 1. hafta: 4 tavuk
• 2. hafta: 4 × 3 = 12 tavuk
• 3. hafta: 4 × 3² = 36 tavuk

Sonuç: 3 hafta sonra 36 tavuk olacaktır.