9.sınıf Bölme ve Bölünebilme Kuralları konu anlatımı Çözümlü Sorular

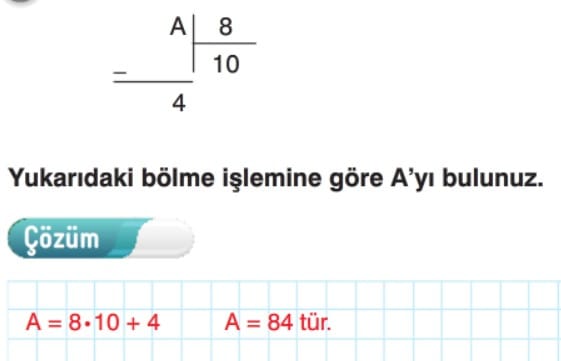
A, B, C, K birer doğal sayı ve B eşit değildir 0 olmak üzere, Bölme işleminde; A: bölünen, B: bölen, C: bölüm, K: kalan diye adlandırılır. Bölme işleminde; A= B . C + K Bölünen sayı; bölen ile bölümün çarpımının, kalan ile toplamına eşittir. K < B Kalan, bölenden küçüktür. Kalan, bölümden küçük ise bölen ile bölümün yerlerinin değiştirilmesi kalanı değiştirmez.
Örnek: Bir bölme işleminde; bölen 12, bölüm 5 ve kalan 2 dir. Buna göre, bölünen sayıyı bulalım.
Çözüm: Bölünen sayı, bölen ile bölümün çarpımına kalanın eklenmesiyle bulunur. Bir bölme işleminde; bölen 12, bölüm 5 ve kalan 2 olduğuna göre, bölünen sayı, 12-5+ 2:60 +2:62 dir.
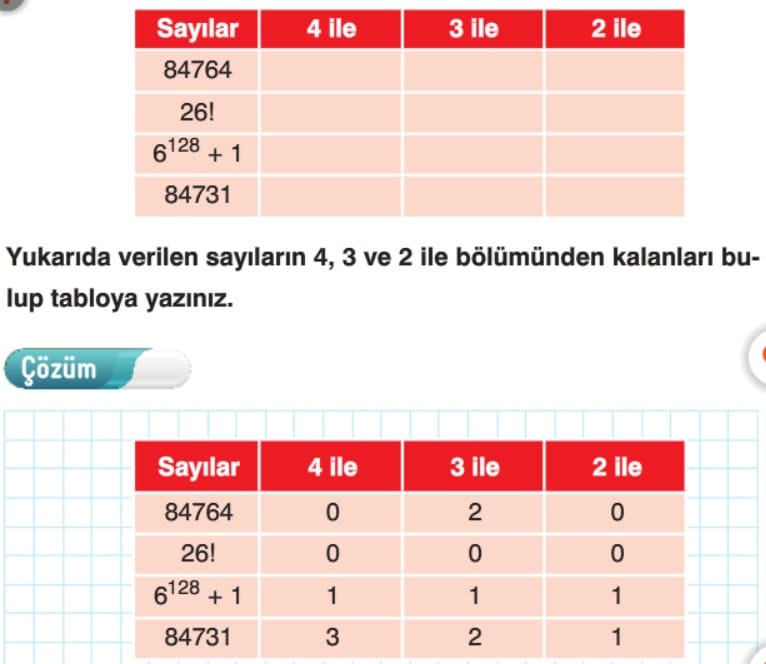
Çift sayılar 2 ile tam bölünür. Tek sayıların 2 ile bölümünden elde edilen kalan 1 dir.
Örnek: 100, 402, 146, 24, 7778 sayıları çift olduğu için 2 ile tam olarak bölünebilir.
Örnek: 41, 143, 215, 1317, 99 sayıları tek olduğu için 2 ile tam olarak bölünemez. Bu sayıların 2 ile bölümlerinden kalan 1 dir.
Örnek: 651 sayısı 3 ile tam bölünür. Çünkü, bu sayının rakamlarının toplamı olan 6 + 5 + 1 = 12 sayısı 3 ün tam katıdır.
Örnek: 708325 sayısının 3 ile bölümünden kalanı bulalım: 7 + 0 + 8 + 3 + 2 + 5 z 25 sayısının 3 ile bölümünden kalan 1 olduğu için, 708325 sayısının 3 ile bölümünden kalan da 1 dir.
Örnek: Dört basamaklı 347A doğal sayısı 3 ile tam bölünebildiğine göre, A nın alabileceği değerleri bulalım.
Onlar basamağındaki rakamı ile birler basamağındaki rakamının (son iki rakam) belirttiği sayı, 4 ün katı olan sayılar, 4 ile tam bölünebilir.
Örnek: 9327 sayısının 4 ile bölümünden kalanı bulalım: 9327 sayısının onlar basamağındaki rakam ile birler basamağındaki rakamın belirttiği sayı 27 dir. 27 nin 4 ile bölümünden kalan 3 olduğu için, 9327 sayısının 4 ile bölümünden kalan da 3 tür.
Örnek: Beş basamaklı 179A6 sayısı 4 ile tam bölünebilen bir sayı olduğuna göre, A nın kaç farklı değer alacağını bulalım.
Çözüm: 179A6 sayısı 4 ile bölünebildiğine göre, A6 sayısı 4 ün katıdır. Buna göre, A6 = 4-k, k e N olmalıdır.
k=4 için A=1
k=9 için A=3
k=14 için A=5
k=19 için A=7
k=24 için A=9 olur.
k nın diğer değerleri için A bulunamayacağından, A rakamı 5 farklı değer alabilir.
Birler basamağında 0 veya 5 rakamı bulunan sayılar 5 ile tam bölünürler. Bir sayının 5 ile bölümünden kalan, 0 sayının birler basamağındaki rakamın 5 ile bölümünden kalandır.
Örnek: Dört basamaklı 73mn sayısı 5 ile tam olarak bölünebilmektedir. Buna göre, m + n toplamının en çok kaç olacağını bulalım.
Çözüm: 73mn sayısı 5 ile tam olarak bölünebildiğine göre, n rakamı 0 veya 5 tir. m + n nin en büyük değeri istendiğine göre, m = 9 ve n = 5 olmalıdır. Buna göre, m + n :9 + 5= 14 olur.
Yüzler, onlar ve birler basamağındaki rakamların (son üç rakam) belirttiği sayı, 8 in katı olan sayılar, 8 ile tam bölünebilir. Bir sayının 8 ile bölümünden kalan, sağdaki son üç rakamın belirttiği sayının 8 ile bölümünden kalana eşittir.
Örnek: 9024 sayısının son üç rakamının belirttiği 24 sayısı 8 ile tam bölünebildiği için, 9024 sayısı da 8 ile tam olarak bölünebilir.
Örnek: 11 019 sayısının son üç rakamının belirttiği 19 sayısı 8 ile bölündüğünde 3 kaldığı için 11 019 sayısı da 8 ile bölündüğünde 3 kalır.
Rakamlarının toplamı 9 un katı olan sayılar 9 ile tam bölünür. Bir sayının 9 ile bölümünden kalan, o sayının rakamlarının toplamının 9 ile bölümünden kalandır.
Örnek: 280 sayısının rakamlarının toplamı olan 10 sayısı 9 ile bölündüğünde 1 kaldığı için 280 sayısı da 9 ile bölündüğünde 1 kalır.
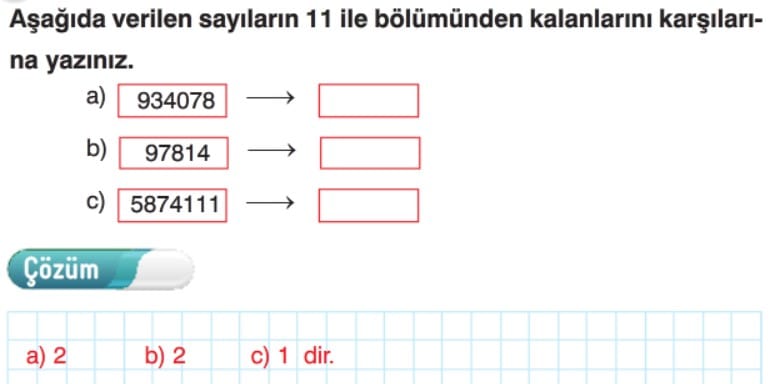
Sayının rakamları, birler basamağından (sağdan sola) başlayarak +, - olarak işaretlenir. + işaretli sayıların toplamından - işaretli sayıların toplamı çıkarılır. Sonuç 11 in katı ise o sayı 11 ile tam bölünür. Bir sayının rakamları, sağdan sola doğru +, - olarak işaretlenir. + işaretli sayıların toplamından - işaretli sayıların toplamı çıkarılır. Sonucun 11 ile bölümünden kalan o sayının 11 ile bölümünden kalandır.