Tales Teoremi 9. Sınıf Matematik (Yeni Müfredat)
Tales Teoremi, geometri dünyasının temel taşlarından biridir ve bir üçgende paralel doğruların oluşturduğu oranları açıklamaktadır. Bu teorem, bir üçgen içinde veya üçgenin bir uzantısında, paralel doğrular arasında oluşan benzer üçgenlerin kenarları arasındaki orantıyı ifade eder. Tales, üçgenlerde benzerlik ilkesini açıklayarak, birçok geometrik problemin çözümüne ışık tutmuştur. Günlük hayatta bu teorem; mühendislik, harita ölçeklendirme ve mimari tasarımlarda kullanılır. Yeni nesil sorular, bu teoremi hikayeler ve gerçek hayat problemleri ile ilişkilendirerek öğrencilerin analitik düşünme becerilerini geliştirmeyi hedefler.
Tales, Öklid ve Pisagor Teoremleri Testleri
TALES TEOREMİ KONU ANLATIMI
Birinci Tales Teoremi
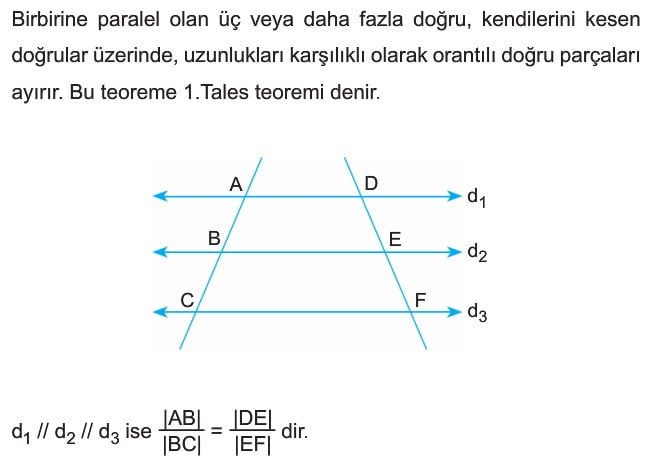
Örnek:
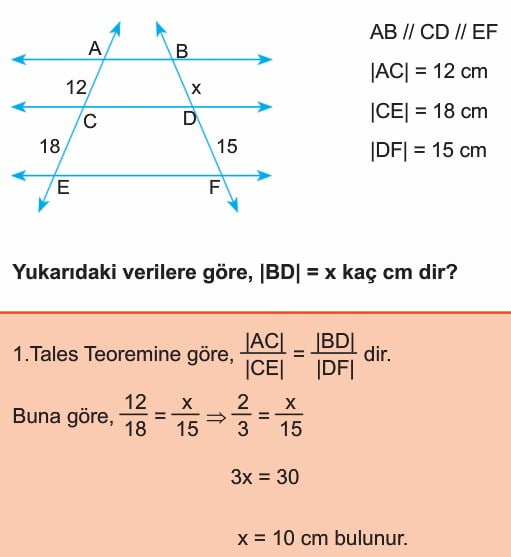
İkinci Tales Teoremi
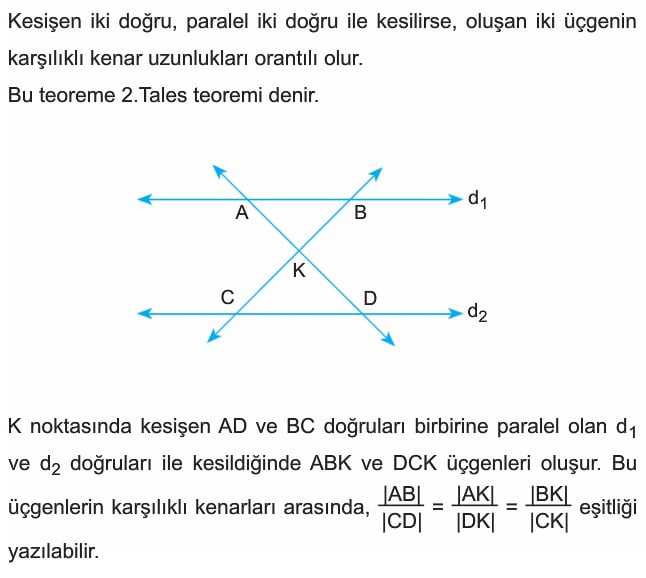
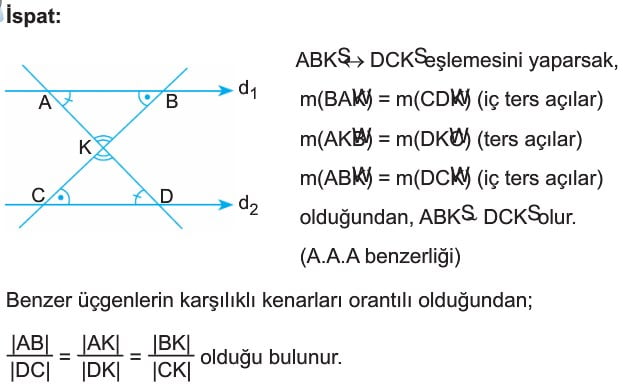

Örnek:
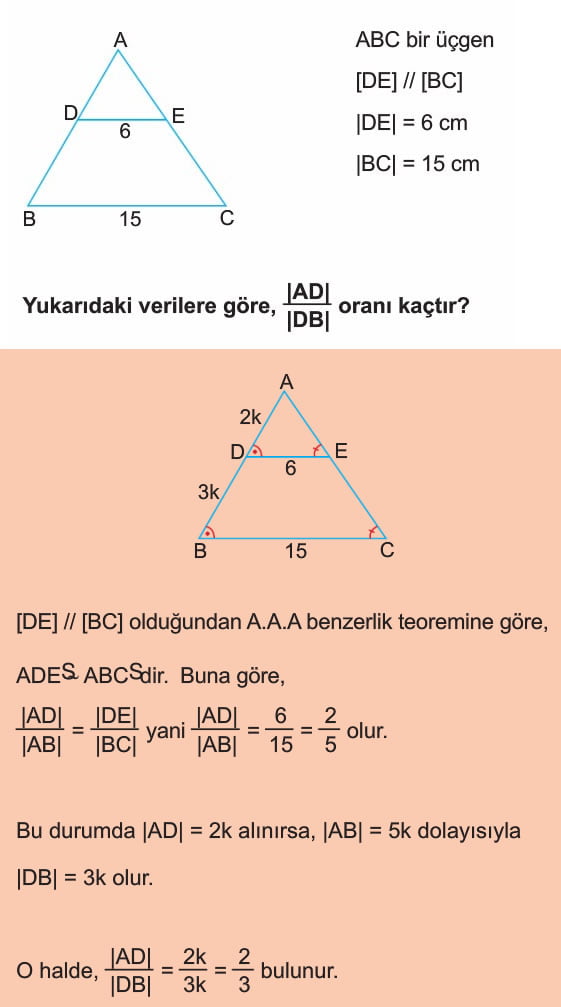
Örnek:
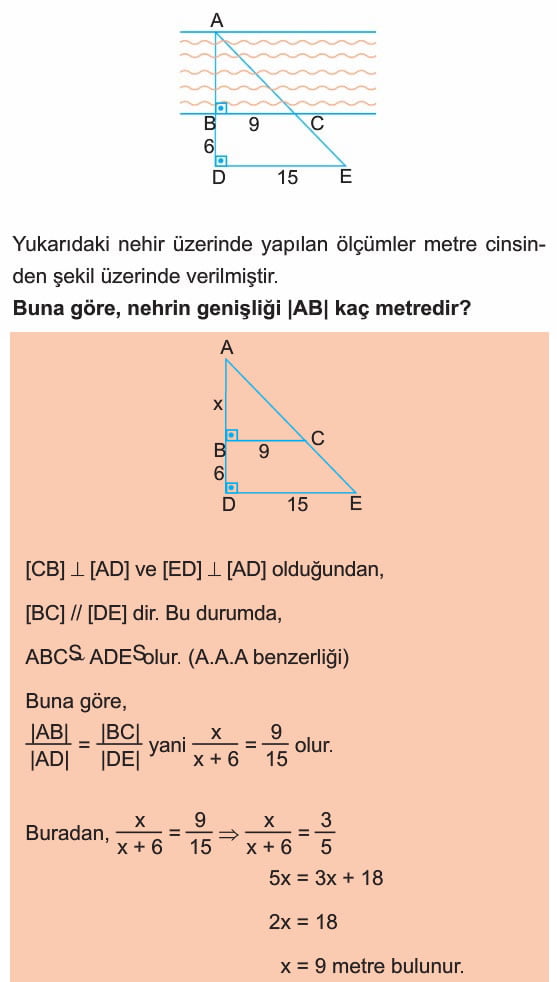
Örnek:
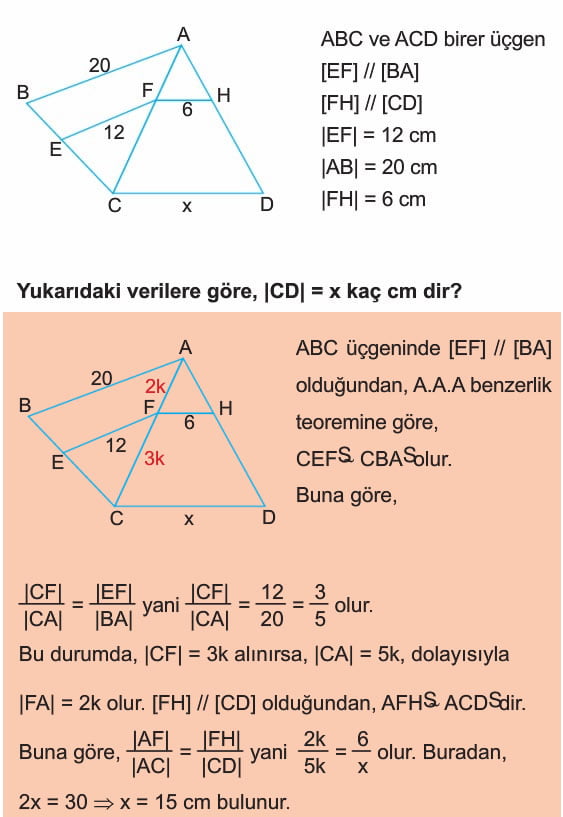
Sonraki Konu: Temel Orantı Teoremi
Çözümlü Örnek Test Soruları
1. Soru:
Bir üçgende paralel iki kenar arasındaki uzunluklar 4 cm ve 8 cm’dir. Küçük üçgende hipotenüs 10 cm olduğuna göre, büyük üçgende hipotenüs kaç cm’dir?
A) 15
B) 18
C) 20
D) 24
E) 30
Çözüm:
Benzer üçgenlerde kenar oranları eşittir:
4/8 = 10/x
1/2 = 10/x
x = 20 cm
Cevap: C
2. Soru:
Bir üçgende [DE] // [BC] olmak üzere, |AD|=6 cm, |AB|=18 cm ve |DE|=8 cm ise |BC| kaç cm’dir?
A) 16
B) 20
C) 24
D) 28
E) 32
Çözüm:
AD/AB = DE/BC
6/18 = 8/|BC|
1/3 = 8/|BC|
|BC| = 24 cm
Cevap: C
3. Soru:
Bir üçgende paralel iki doğru arasındaki uzunluklar 5 cm ve 15 cm’dir. Küçük üçgende bir kenar 7 cm olduğuna göre, büyük üçgende karşılık gelen kenar kaç cm’dir?
A) 14
B) 18
C) 21
D) 24
E) 28
Çözüm:
5/15 = 7/x
1/3 = 7/x
x = 21 cm
Cevap: C
4. Soru:
[KL] // [MN] olan bir üçgende |AK|=9 cm, |KM|=3 cm ve |AN|=15 cm ise |NL| kaç cm’dir?
A) 4
B) 5
C) 6
D) 7
E) 8
Çözüm:
AK/KM = AN/NL
9/3 = 15/|NL|
3 = 15/|NL|
|NL| = 5 cm
Cevap: B
5. Soru:
Bir üçgende paralel iki kenar arasındaki oran 2:5’tir. Küçük üçgende bir kenar 6 cm olduğuna göre, büyük üçgende karşılık gelen kenar kaç cm’dir?
A) 12
B) 15
C) 18
D) 20
E) 25
Çözüm:
2/5 = 6/x
2x = 30
x = 15 cm
Cevap: B
6. Soru:
[PQ] // [RS] olan bir üçgende |XP|=4 cm, |PR|=6 cm ve |XQ|=8 cm ise |QS| kaç cm’dir?
A) 10
B) 12
C) 14
D) 16
E) 18
Çözüm:
XP/PR = XQ/QS
4/6 = 8/|QS|
2/3 = 8/|QS|
|QS| = 12 cm
Cevap: B
7. Soru:
Bir üçgende paralel iki doğru arasındaki uzunluklar 3 cm ve 12 cm’dir. Küçük üçgende hipotenüs 5 cm olduğuna göre, büyük üçgende hipotenüs kaç cm’dir?
A) 15
B) 18
C) 20
D) 24
E) 25
Çözüm:
3/12 = 5/x
1/4 = 5/x
x = 20 cm
Cevap: C
8. Soru:
[DE] // [BC] olan bir üçgende |AD|=7 cm, |DB|=14 cm ve |DE|=9 cm ise |BC| kaç cm’dir?
A) 18
B) 21
C) 24
D) 27
E) 30
Çözüm:
AD/AB = DE/BC
7/(7+14) = 9/|BC|
7/21 = 9/|BC|
1/3 = 9/|BC|
|BC| = 27 cm
Cevap: D
9. Soru:
Bir üçgende paralel iki kenar arasındaki oran 3:7’dir. Küçük üçgende bir kenar 12 cm olduğuna göre, büyük üçgende karşılık gelen kenar kaç cm’dir?
A) 24
B) 26
C) 28
D) 30
E) 32
Çözüm:
3/7 = 12/x
3x = 84
x = 28 cm
Cevap: C
10. Soru:
[KL] // [MN] olan bir üçgende |AK|=10 cm, |KM|=5 cm ve |AN|=18 cm ise |NL| kaç cm’dir?
A) 6
B) 7
C) 8
D) 9
E) 10
Çözüm:
AK/KM = AN/NL
10/5 = 18/|NL|
2 = 18/|NL|
|NL| = 9 cm
Cevap: D
11. Soru:
Bir üçgende paralel iki doğru arasındaki uzunluklar 6 cm ve 24 cm’dir. Küçük üçgende bir kenar 8 cm olduğuna göre, büyük üçgende karşılık gelen kenar kaç cm’dir?
A) 28
B) 30
C) 32
D) 36
E) 40
Çözüm:
6/24 = 8/x
1/4 = 8/x
x = 32 cm
Cevap: C
12. Soru:
[PQ] // [RS] olan bir üçgende |XP|=6 cm, |PR|=9 cm ve |XQ|=14 cm ise |QS| kaç cm’dir?
A) 18
B) 20
C) 21
D) 24
E) 28
Çözüm:
XP/PR = XQ/QS
6/9 = 14/|QS|
2/3 = 14/|QS|
|QS| = 21 cm
Cevap: C
13. Soru:
Bir üçgende paralel iki kenar arasındaki oran 4:9’dur. Küçük üçgende bir kenar 16 cm olduğuna göre, büyük üçgende karşılık gelen kenar kaç cm’dir?
A) 32
B) 34
C) 36
D) 38
E) 40
Çözüm:
4/9 = 16/x
4x = 144
x = 36 cm
Cevap: C
14. Soru:
[DE] // [BC] olan bir üçgende |AD|=8 cm, |AB|=24 cm ve |DE|=10 cm ise |BC| kaç cm’dir?
A) 25
B) 28
C) 30
D) 32
E) 36
Çözüm:
AD/AB = DE/BC
8/24 = 10/|BC|
1/3 = 10/|BC|
|BC| = 30 cm
Cevap: C
15. Soru:
Bir üçgende paralel iki doğru arasındaki uzunluklar 5 cm ve 20 cm’dir. Küçük üçgende hipotenüs 13 cm olduğuna göre, büyük üçgende hipotenüs kaç cm’dir?
A) 39
B) 42
C) 45
D) 48
E) 52
Çözüm:
5/20 = 13/x
1/4 = 13/x
x = 52 cm
Cevap: E
16. Soru
Bir üçgenin kenar uzunlukları 4 cm, 6 cm ve 8 cm’dir. Bu üçgene paralel doğrularla oluşturulan benzer üçgende en kısa kenar 8 cm ise, diğer kenarlar kaç cm’dir?
a) 12 ve 16
b) 10 ve 14
c) 16 ve 20
d) 18 ve 24
e) 20 ve 25
Çözüm:
Oran: 8 ÷ 4 = 2
Diğer kenarlar:
6 × 2 = 12, 8 × 2 = 16
Cevap: a) 12 ve 16
17. Soru
Bir üçgende paralel doğrular arasındaki uzunluklar 3 cm ve 6 cm’dir. Küçük üçgende hipotenüs 9 cm olduğuna göre, büyük üçgende hipotenüs kaç cm’dir?
a) 12
b) 15
c) 18
d) 20
e) 24
Çözüm:
Oran: 6 ÷ 3 = 2
Büyük üçgenin hipotenüsü:
9 × 2 = 18
Cevap: c) 18
18. Soru
Tales Teoremine göre, bir üçgende kenar uzunlukları 5 cm, 8 cm ve 10 cm’dir. Bu üçgene paralel doğrularla oluşturulan büyük üçgende en uzun kenar 20 cm ise, diğer kenarlar kaç cm’dir?
a) 10 ve 16
b) 15 ve 24
c) 14 ve 18
d) 20 ve 25
e) 12 ve 19
Çözüm:
Oran: 20 ÷ 10 = 2
Diğer kenarlar:
5 × 2 = 10, 8 × 2 = 16
Cevap: a) 10 ve 16
19. Soru
Bir üçgenin kenar uzunlukları 7 cm, 10 cm ve 14 cm’dir. Bu üçgene paralel doğrularla oluşturulan büyük üçgende orta kenar 20 cm ise, diğer kenarlar kaç cm’dir?
a) 10 ve 28
b) 14 ve 28
c) 21 ve 42
d) 12 ve 18
e) 16 ve 24
Çözüm:
Oran: 20 ÷ 10 = 2
Diğer kenarlar:
7 × 2 = 14, 14 × 2 = 28
Cevap: b) 14 ve 28
20. Soru
Bir üçgenin küçük üçgen kısmında paralel doğrularla oluşturulan kenarlar 3 cm ve 6 cm’dir. Büyük üçgenin hipotenüsü 15 cm ise, küçük üçgenin hipotenüsü kaç cm’dir?
a) 5
b) 7
c) 9
d) 10
e) 12
Çözüm:
Oran: 6 ÷ 3 = 2
Küçük üçgenin hipotenüsü:
15 ÷ 2 = 7.5 (Yuvarlanmış bir değer bulunursa daha ayrıntı verebiliriz.)
Cevap: b)





Good
20 tane cevaplı thales benzerliği sorusu nasıl bulabilirim ?