Fizikte büyüklükler iki ana gruba ayrılır: skaler ve vektörel nicelikler. Skaler nicelikler, yalnızca büyüklük bilgisi taşıyan değerlerdir ve yön belirtmezler. Örneğin, uzunluk, sıcaklık, kütle gibi nicelikler skalerdir. Vektörel nicelikler ise hem büyüklük hem de yön bilgisi içerir; kuvvet, hız, ve ivme gibi nicelikler bu kategoriye girer. Vektörel nicelikler yönleriyle birlikte ifade edildiğinde anlam kazanır. Bu nedenle, günlük hayatta ve bilimsel hesaplamalarda skaler ve vektörel niceliklerin doğru tanımlanması ve anlaşılması önemlidir.

9. Sınıf Skaler ve Vektörel Nicelikler Testleri

9.Sınıf Skaler ve Vektörel Nicelikler Ders Notu (Yeni Müfredat)

Kuvvet, hız gibi bazı büyüklükleri belirtmek için yön de gereklidir. Oysa kütle, uzunluk gibi büyüklükler için böyle bir koşul yoktur. Bu nedenle fizikte büyüklükler skaler ve vektörel olmak üzere ikiye ayrılmıştır.
Belirtirken yön gerektirmeyen, yalnızca bir sayı ve birimle belirtilebilen büyüklüklere skaler büyüklük, sayı ve birimin yanında bir de yöne sahip olan büyüklüklere vektörel büyüklükler denir.

Skaler Büyüklükler

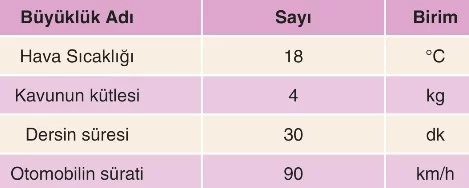
Aşağıda skaler niceliklere bazı örnekler verilmiştir.

Sıcaklık , Zaman , Kütle , Özkütle , Sürat , Uzunluk , Hacim

Vektörel Büyüklükler

Fizikte bazı büyüklüklerin ifade edilmesi sırasında büyüklüğün sayısal değeri ve biriminin yazılması yeterli olur. Bu tür büyüklüklere skaler büyüklükler denir. Skaler büyüklüklerde yön yoktur.

Odanın sıcaklığı 24°C dir.
Sınav süresi 45 dakikadır.
Onur’un kütlesi 44 kg dır.
Motorun gücü 100 watt tır.

Verdiğimiz örneklerde ölçü sayısını ve birimini belirtmek büyüklüğün tam olarak ifade edilmesi anlamına gelir. çünkü sıcaklık, zaman, kütle, güç, skaler büyüklüklerdir.

Bazı büyüklükler ise yalnızca ölçü sayıları ve birimlerinin verilmesi ile tam olarak ifade edilememiş olur. Bu tür büyüklüklerde sayı ve birime ilave olarak yön de belirtilmelidir. Bu tür yönlü büyüklüklere vektörel büyüklükler denir.

Vektörel işlemlerde sonucun fiziksel bir nicelik olabilmesi için:

• İki vektör toplanabilir veya çıkarılabilir.
• Bir vektör bir skaler sayıyla çarpılabilir.
• Bir vektör bir skaler sayıya bölünebilir.
• Bir vektör bir vektöre bölünemez. Bölümü fiziksel bir nicelik olamaz.

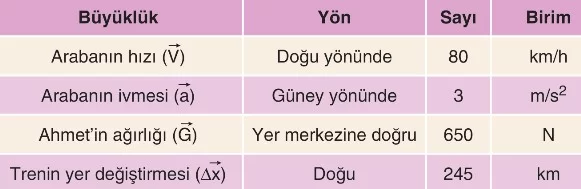
Vektörel büyüklüklere hız, ivme, yer değiştirme, ağırlık, kuvvet örnek olarak verilebilir. Vektörel büyüklükler vektör adı verilen yönlü doğru parçaları ile gösterilirler.

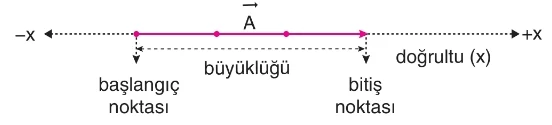
Her vektörün,

1) Doğrultu
2) Yön
3) Büyüklük
4) Başlangıç Noktası olmak üzere dört özelliği vardır.

Doğrultu ve yön aynı kavramlar değildir. Her doğrultuda iki yön vardır. Örneğin kuzey güney bir doğrultu, kuzey bir yön, güney başka bir yöndür.

Aşağıda vektörel niceliklere bazı örnekler verilmiştir.

Hız , Kuvvet , İvme , Ağırlık , Yer değiştirme , Konum

Skaler ve Vektörel Büyüklükler Tonguç

Çözümlü Örnek Test Soruları

Soru 1:
Ahmet, düz bir yol boyunca yürüyüş yapmaktadır. İlk olarak 4 km kuzey yönünde ilerledikten sonra 3 km doğuya doğru yol alır. Bu durumda Ahmet’in toplam aldığı yol ve yer değiştirmesi nedir?

A) Yol: 7 km, Yer değiştirme: 5 km
B) Yol: 5 km, Yer değiştirme: 4 km
C) Yol: 4 km, Yer değiştirme: 3 km
D) Yol: 7 km, Yer değiştirme: 4 km

Çözüm:
Ahmet’in toplam aldığı yol skaler bir büyüklük olup, gittiği mesafelerin toplamıdır: 4 km + 3 km = 7 km. Yer değiştirme ise başlangıç noktasından bitiş noktasına olan doğrusal mesafedir. Bu durumda, yer değiştirme formülü uygulanır:
Yer Değiştirme = √(4² + 3²) = √(16 + 9) = √25 = 5 km.
Cevap: A

Soru 2:
Bir cisim sabit bir hızla doğu yönünde 60 m ilerliyor, ardından güney yönüne dönerek 80 m daha hareket ediyor. Cismin aldığı toplam yol ve yer değiştirme mesafesi ne olur?

A) Yol: 140 m, Yer değiştirme: 100 m
B) Yol: 140 m, Yer değiştirme: 80 m
C) Yol: 80 m, Yer değiştirme: 60 m
D) Yol: 100 m, Yer değiştirme: 140 m

Çözüm:
Toplam yol, cismin hareket ettiği mesafelerin toplamıdır: 60 m + 80 m = 140 m. Yer değiştirme ise başlangıç noktasından bitiş noktasına olan doğrusal mesafedir:
Yer Değiştirme = √(60² + 80²) = √(3600 + 6400) = √10000 = 100 m.
Cevap: A

Soru 3:
Bir öğrenci, okuldan evine doğru 5 km doğuya, ardından 2 km kuzeye doğru hareket ediyor. Bu durumda öğrencinin aldığı toplam yol ve yer değiştirme nedir?

A) Yol: 5 km, Yer değiştirme: 2 km
B) Yol: 2 km, Yer değiştirme: 5 km
C) Yol: 7 km, Yer değiştirme: 5.39 km
D) Yol: 7 km, Yer değiştirme: 7 km

Çözüm:
Toplam yol, skaler olarak 5 km + 2 km = 7 km. Yer değiştirme ise iki mesafe arasındaki doğrusal uzaklıktır:
Yer Değiştirme = √(5² + 2²) = √(25 + 4) = √29 ≈ 5.39 km.
Cevap: C

Soru 4:
Bir arabanın saatte 50 km hızla doğuya doğru ilerlediğini düşünelim. Bu hız ifadesi hangi tür niceliktir?

A) Skaler
B) Vektörel
C) Hem skaler hem vektörel
D) Belirtilmemiş

Çözüm:
Hız, büyüklük ve yön içerdiği için vektörel bir niceliktir.
Cevap: B

Soru 5:
Bir öğrenci sırasıyla 3 km batıya, 4 km güneye ve 5 km doğuya doğru hareket ediyor. Bu durumda öğrencinin toplam aldığı yol ve yer değiştirme mesafesi nedir?

A) Yol: 12 km, Yer değiştirme: 6.4 km
B) Yol: 12 km, Yer değiştirme: 5 km
C) Yol: 8 km, Yer değiştirme: 12 km
D) Yol: 7 km, Yer değiştirme: 8 km

Çözüm:
Toplam yol skaler olup tüm adımların toplamıdır: 3 km + 4 km + 5 km = 12 km. Yer değiştirme ise net olarak hesaplanır:
Batı ve doğu yönleri birbirini dengeler ve yer değiştirme güney yönünde kalır:
Yer Değiştirme = √(0² + 4²) = 4 km.
Cevap: A