Sayı kümeleri, matematiğin temel yapı taşlarıdır ve bu kümeler belirli özelliklere sahip olarak sınıflandırılır. 9. sınıf matematik müfredatında, sayı kümelerinin sıralı olma ve dört işlemle ilgili kapalı olma özellikleri üzerinde durulur. Bu özellikler, sayı kümeleri arasındaki ilişkileri anlamak ve bu ilişkileri matematiksel işlemlerle ifade edebilmek için büyük önem taşır. Öğrencilerin bu kavramları anlaması, matematiksel düşünme becerilerini geliştirmelerine ve daha karmaşık matematiksel problemlerde başarılı olmalarına yardımcı olur.

9. Sınıf Sayı Kümelerinin Özellikleri Testleri

9. SINIF SAYI KÜMELERİNİN ÖZELLİKLERİ DERS NOTU (YENİ MÜFREDAT)

• Sayı Kümelerinin Sıralı Olması ve Herhangi İki Sayı Arasındaki Sayıları Belirleme
• Sayı Kümelerinin Dört İşleme Göre Kapalılığı

Sayı Kümelerinin Sıralı Olması ve Herhangi İki Sayı Arasındaki Sayıları Belirleme

• Bir sayı kümesindeki herhangi iki sayı arasında, aynı sayı kümesinden başka bir sayının yer alması o kümenin “arada olma” özelliğine sahip olduğunu gösterir. Örneğin, bir okul müdürü sınıf kapasitesini belirlerken sınıfın alabileceği maksimum ve minimum öğrenci sayısını belirler ve sınıfları buna göre yerleştirir.
• Doğal sayılar, tam sayılar, rasyonel sayılar ve gerçek sayılar sıralı kümelerdir. Ancak, doğal sayılar ve tam sayılar kümelerinde “arada olma” özelliği yoktur.
  2 ile 3 doğal sayıları arasında bir doğal sayı bulunmaz.
  -3 ile -2 tam sayıları arasında bir tam sayı yoktur.
• Buna karşın, rasyonel sayılar ve gerçek sayılar kümelerinde “arada olma” özelliği vardır. Herhangi iki rasyonel sayı veya gerçek sayı arasında istenilen sayıda rasyonel ya da gerçek sayı bulunabilir.

a, b, c, d ∈ R – {0} olmak üzere

1. a < b ⇔ a + c < b + c

2.
a < b ve c > 0 ise a·c < b·c
a < b ve c < 0 ise a·c > b·c

3.

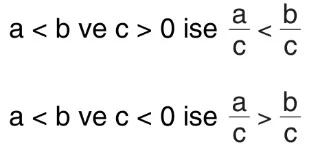
4. a < b ve b < c ise a < c

5.

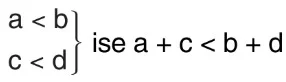
6. 

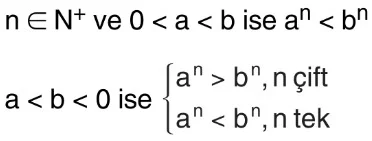
7.
a ve b aynı işaretli ve a < b ise

8. n > 1, n ∈ N⁺ ve 0 < a < 1 ise aⁿ < a

Karşıt örnek sunma, bir genellemenin her durumda geçerli olmadığını ispatlamak için kullanılan bir matematiksel yöntemdir. Bir önermenin doğru olmadığını kanıtlamak için, o önermeye uymayan tek bir örnek bulmak yeterlidir. Bu karşıt örnek, genellemenin tüm durumları kapsamadığını gösterir ve önermeyi çürütür.

Doğal sayılar, tam sayılar, rasyonel sayılar ve gerçek sayılar sıralı kümelerdir. Ancak bu kümeler arasında arada olma özelliği açısından farklılıklar bulunur:

• Doğal sayılar (N): Ardışık iki doğal sayı arasında başka bir doğal sayı yer almaz. Yani, bir doğal sayıdan sonra gelen bir sonraki doğal sayı arasında başka bir doğal sayı bulunmaz. Bu nedenle doğal sayılar kümesinde arada olma özelliği mevcut değildir.
• Tam sayılar (Z): Benzer şekilde, ardışık iki tam sayı arasında da başka bir tam sayı yer almaz. Örneğin, -3 ile -2 arasında herhangi bir tam sayı yoktur. Bu nedenle tam sayılar kümesinde arada olma özelliği yoktur.
• Rasyonel sayılar: Herhangi iki rasyonel sayı arasında, ne kadar küçük veya büyük olursa olsun, istenildiği kadar rasyonel sayı bulunabilir. Yani, bu kümede arada olma özelliği vardır.
• Gerçek sayılar: Rasyonel sayılarda olduğu gibi, iki gerçek sayı arasında sonsuz sayıda gerçek sayı bulunabilir. Bu da R kümesinin arada olma özelliğine sahip olduğunu gösterir.

Sonuç olarak, Q (rasyonel sayılar) ve R (gerçek sayılar) kümeleri arada olma özelliğine sahiptir, ancak N (doğal sayılar) ve Z (tam sayılar) kümeleri bu özelliğe sahip değildir.

Sayı Kümelerinin Sıralı Olması ve Herhangi İki Sayı Arasındaki Sayıları Belirleme Çözümlü Sorular

Sayı Kümelerinin Dört İşleme Göre Kapalılığı

Bir sayı kümesinde yapılan dört işlem sonucunda elde edilen değerlerin yine o küme içinde kalması, algoritmaların ve formüllerin geliştirilmesi sırasında tutarlılığı sağlar. Bu özellik, sayı kümeleri ile ilgili işlemlerin yapısal özelliklerinin anlaşılmasında önemli bir role sahiptir ve çeşitli matematiksel yapıların temelini oluşturur.

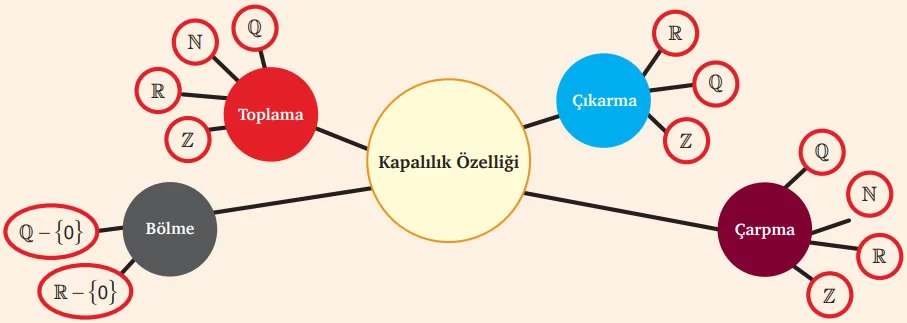
Kapalılık Özelliği

Bir kümedeki herhangi bir eleman bir işleme girdiğinde elde edilen sonuç yine aynı kümenin elemanı ise, bu küme o işleme göre kapalıdır. Kapalılık özelliğini kanıtlamak için “doğrudan ispat metodu” kullanılır. Eğer kapalılık özelliği sağlanmıyorsa, bunun ispatı için en basit yöntem “karşıt örnek verme” metodudur.

Örnek:
N = {0, 1, 2, 3, …} üzerinde dört işlem için kapalılık özelliğini inceleyelim:

1. Toplama: a ve b ∈ N olsun. İki doğal sayının toplamı yine bir doğal sayıdır, yani a + b ∈ N. Dolayısıyla, N kümesi toplama işlemine göre kapalıdır. Bu şekilde, dört işlem için kapalılık özelliği değerlendirilir ve sayılar kümeleri üzerinde hangi işlemlerin kapalı olduğu belirlenir.

2. Çıkarma: 1 ve 4 doğal sayıları için, 1 – 4 = -3 olur. Ancak -3 doğal sayılar kümesine (N) ait değildir. Bu durumda, N kümesi çıkarma işlemine göre kapalı değildir.

3. Çarpma: a ve b ∈ N olsun. İki doğal sayının çarpımı da yine bir doğal sayı olacaktır. Yani a · b ∈ N’dir. Bu durumda, N kümesi çarpma işlemine göre kapalıdır.

4. Bölme: 1 ve 4 doğal sayıları için, 1 ÷ 4 = 1/4 olur. Fakat 1/4 bir doğal sayı değildir. Bu nedenle, N kümesi bölme işlemine göre kapalı değildir.

Bir sayı kümesi ve bir işlem verildiğinde, kapalılık özelliğinin sağlanıp sağlanmadığını ispatlamak için Doğrudan İspat Metodu sıkça kullanılır.

Örnek: A = {x | x = 5k, k ∈ N} = {0, 5, 10, …} kümesinin toplama işlemine göre kapalılığını inceleyelim.
İspat: x₁ ve x₂ ∈ A alalım.
x₁ = 5k₁
x₂ = 5k₂ olsun.
x₁ + x₂ = 5k₁ + 5k₂ = 5(k₁ + k₂) ∈ A olur. Bu durumda A kümesi toplama işlemine göre kapalıdır.

NOT: Bir kümenin bir işleme göre kapalı olmadığını “Aksi Örnek Verme” yöntemiyle inceleyebiliriz.

Örnek: A = {x | x = 5k, k ∈ N} = {0, 5, 10, …} kümesinin bölme işlemine göre kapalılığını inceleyelim.
5 ve 10 ∈ A alalım:
5 ÷ 10 = 1/2 ∉ A.
Bu durumda A kümesi bölme işlemine göre kapalı değildir.

Sayı Kümelerinin Dört İşleme Göre Kapalılığı Çözümlü Sorular

Çözümlü Test Soruları

Soru 1:
Aşağıdakilerden hangisi irrasyonel sayı değildir?
A) √2
B) π
C) 0,333…
D) √5

Çözüm:
Doğru cevap C) 0,333…‘dür. Bu sayı 1/3’e eşittir ve rasyonel sayıdır. Diğer seçeneklerdeki sayılar irrasyoneldir.

Soru 2:
Tam sayılar kümesi (ℤ) ile ilgili aşağıdaki ifadelerden hangisi yanlıştır?
A) Toplama işlemine göre kapalıdır
B) Çarpma işlemine göre kapalıdır
C) Bölme işlemine göre kapalıdır
D) Çıkarma işlemine göre kapalıdır

Çözüm:
Doğru cevap C) Bölme işlemine göre kapalıdır‘dır. Tam sayılar bölme işlemine göre kapalı değildir (örneğin 3 ÷ 2 = 1,5 tam sayı değildir).

Soru 3:
Aşağıdaki sayı kümelerinden hangisi diğerlerini kapsar?
A) Doğal sayılar (ℕ)
B) Tam sayılar (ℤ)
C) Rasyonel sayılar (ℚ)
D) Gerçek sayılar (ℝ)

Çözüm:
Doğru cevap D) Gerçek sayılar (ℝ)‘dır. Gerçek sayılar kümesi diğer tüm sayı kümelerini kapsar.

Soru 4:
I. Her rasyonel sayı gerçek sayıdır
II. Her irrasyonel sayı tam sayıdır
III. Her doğal sayı tam sayıdır
Yukarıdaki ifadelerden hangileri doğrudur?

A) Yalnız I
B) I ve II
C) I ve III
D) I, II ve III

Çözüm:
Doğru cevap C) I ve III‘tür. II. ifade yanlıştır çünkü irrasyonel sayılar tam sayı değildir.

Soru 5:
Aşağıdaki işlemlerden hangisinin sonucu bir irrasyonel sayıdır?
A) √9 + √16
B) √2 × √8
C) π + 1
D) 0,5 ÷ 2

Çözüm:
Doğru cevap C) π + 1‘dir. π irrasyonel olduğu için π + 1 de irrasyoneldir. Diğer seçenekler:
A) 3 + 4 = 7 (tam sayı)
B) √16 = 4 (tam sayı)
D) 0,25 (rasyonel)

Soru 6:
Reel sayılarla ilgili aşağıdaki ifadelerden hangisi doğrudur?
A) Sayı doğrusunda boşluklar vardır
B) Rasyonel ve irrasyonel sayıların birleşimidir
C) Sonlu elemanlı bir kümedir
D) Yalnızca kesirli sayılardan oluşur

Çözüm:
Doğru cevap B) Rasyonel ve irrasyonel sayıların birleşimidir‘dir. Reel sayılar kümesi bu iki kümenin birleşimidir.