Sayı kümeleri ve sayı kümelerinin gösterimi, 9. sınıf matematik müfredatında önemli bir yere sahip olan temel kavramlardır. Bu konular, öğrencilerin matematiksel düşünme becerilerini geliştirmeleri, sayıları sınıflandırmayı öğrenmeleri ve farklı sayı kümeleri arasındaki ilişkileri anlamaları açısından kritik öneme sahiptir. Bu makalede, sayı kümeleri ve bu kümelerin sembollerle nasıl ifade edildiğini ayrıntılarıyla ele alacağız.

9. Sınıf Sayı Kümeleri ve Sayı Kümelerinin Gösterimi Testleri

9. Sınıf Sayı Kümeleri Ders Notu (Yeni Müfredat)

Matematiksel sembolleri kullandığımızda matematiksel ifadeler daha net ve anlaşılır şekilde ifade edilebilir. Küme gösteriminde de kümenin elemanlarını tanımlamak veya elemanların özelliklerini daha anlaşılır bir şekilde ifade etmek için matematiksel semboller kullanılır.

KÜME NEDİR?

İyi tanımlanmış (elemanları belli olan) birbirinden farklı nesneler topluluğuna (yığınına) küme denir. Kümeyi oluşturan her nesneye o kümenin elemanı denir.

• Elemandır sembolü ∈ ile gösterilir.
• Elemanı değildir sembolü ∉ ile gösterilir.
• Bir A kümesinin eleman sayısı s(A) şeklinde gösterilir.

SAYI KÜMELERİNİN GÖSTERİMİ

Kümeler genel olarak üç farklı yolla gösterilir:

Liste Yöntemi: Kümeyi oluşturan bütün elemanların { } parantezinin içinde aralarında virgül kullanılarak gösterilmesidir.

Venn Şeması: Kümeyi oluşturan bütün elemanların genel olarak geometrik bir şekil içerisinde önüne “∈” konularak gösterilmesidir.

Ortak Özellik Yöntemi: Kümenin bütün elemanlarının sahip olduğu ortak özelliğin matematiksel veya sözel bir ifade ile gösterilmesidir.

A = {x | …. } kümesinde;
“x |”, x öyleki şeklinde okunur.

Küme Tanımı ve Küme Gösterim Yöntemleri Çözümlü Sorular

BOŞ KÜME

• Elemanı olmayan kümeye boş küme denir. Boş kümenin gösterimi “∅” şeklinde olup liste yöntemi ile gösterimi { } biçimindedir. Boş kümenin eleman sayısı sıfırdır.
• Tanımlanan kümenin herhangi bir elemanı bulunamıyor ise o küme, boş kümedir.
  Örnek: {Ğ ile başlayan günler} = ∅ dir

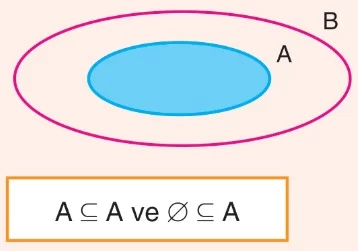
ALT KÜME

• A ve B herhangi iki küme olmak üzere, A kümesinin her elemanı aynı zamanda B kümesinin elemanı oluyor ise A kümesine B kümesinin alt kümesi denir.
  A ⊆ B ile gösterilir.
• n elemanlı bir kümenin 2ⁿ tane alt kümesi vardır.
  Bu kümeler B’yi kapsar A şeklinde de söylenir.
  B ⊇ A şeklinde gösterilir.

SONLU VE SONSUZ KÜME

• Eleman sayısı sayılabilir çoklukta olan kümelere sonlu küme denir.
• Sonlu olmayan kümelere sonsuz küme denir.

Örneğin rakamlar kümesi sonlu bir küme iken doğal sayılar kümesi sonsuz kümedir.

Boş Küme, Sonlu ve Sonsuz Küme, Alt Küme Çözümlü Sorular

Gerçek Sayılar Kümesi (ℝ)

• Üzerinde çalışılan kümelere ait tüm elemanları kapsayan kümeye evrensel küme denir ve E harfi ile gösterilir.
• Gerçek sayılar kümesi (ℝ); doğal sayılar (ℕ), tam sayılar (ℤ), rasyonel sayılar (ℚ) ve irrasyonel sayılar (ℚ’) kümelerini kapsayan en geniş kümedir. Gerçek sayılar kümesi, evrensel küme olarak ifade edilebilir.

Örnek: A = {1, 2, 3} ve B = {3, 4, 5, 6} olmak üzere,
I. { x ∣ x < 6, x ∈ N }
II. { x ∣ x < 10, x ∈ Z⁺ }
III. { x ∣ x² < 40, x ∈ N }

kümelerinden hangileri A ve B kümeleri için bir evrensel küme belirtir?

Çözüm:

• I. küme: {x ∣ x < 6, x ∈ N} = {1, 2, 3, 4, 5}
  6 sayısı bu kümede yok. Bu nedenle evrensel küme olamaz.
• II. küme: {x ∣ x < 10, x ∈ Z⁺} = {1, 2, 3, 4, 5, 6, 7, 8, 9}
  A ve B kümelerinin tüm elemanlarını kapsar. Evrensel küme olabilir.
• III. küme: { x ∣ x² < 40, x ∈ N } = { 1, 2, 3, 4, 5, 6 }
  A ve B kümelerinin tüm elemanlarını kapsar. Evrensel küme olabilir.

Sonuç: II ve III kümeleri A ve B kümeleri için evrensel küme belirtir.

KÜMELERDE İŞLEMLER

Kümelerde Birleşim ve Kesişim İşlemi

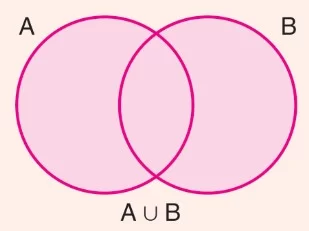
• A ve B iki küme olsun. A ve B kümelerinin tüm elemanlarının oluşturduğu kümeye, A ve B kümelerinin birleşim kümesi denir.
  A ∪ B ile gösterilir.
  A ∪ B = {x | x ∈ A veya x ∈ B}’dir.

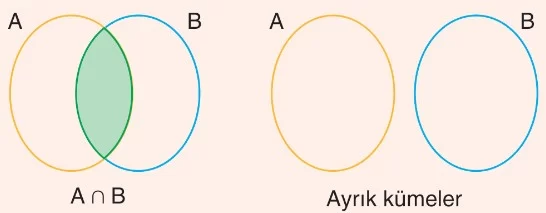
• A ve B iki küme olsun. A ve B kümelerinin ortak elemanlarının oluşturduğu kümeye, A ve B kümelerinin kesişim kümesi denir.
  A ∩ B ile gösterilir.
  A ∩ B = {x | x ∈ A ve x ∈ B}’dir.
• A ∩ B = Ø ise A ve B kümelerinin ortak elemanı yoktur. Bu durumda A ve B kümelerine ayrık kümeler denir.

Evrensel Küme ve Bir Kümeyi Tümleyeni

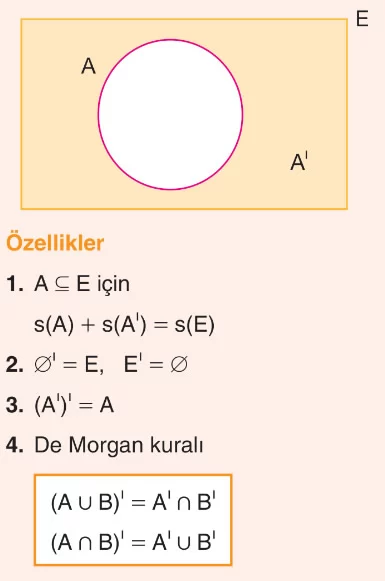
• Belirli bir konuda üzerinde işlem yapılan, bütün kümeleri içine alan, boş kümeden farklı en geniş kümeye evrensel küme denir. E harfi ile gösterilir.
• A ⊆ E olmak üzere, evrensel kümeye dahil olup da A kümesinde olmayan elemanların kümesine A kümesinin tümleyeni denir. A’ ile gösterilir.

Kümelerde Fark İşlemi

• A ve B iki küme olsun. A kümesinde olup B kümesinde olmayan elemanların oluşturduğu kümeye, A fark B kümesi denir.
• A − B veya A \ B ile gösterilir.

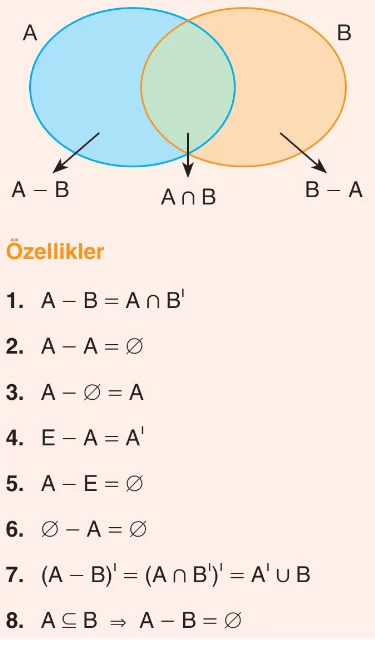
Kümelerde İşlemler Çözümlü Sorular