Rakam: Sayıları ifade etmeye yarayan sembollere rakam denir.
Rakamlar kümesi {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} dur.

Sayı: Rakamların bir çokluk belirtecek şekilde bir araya gelmesiyle oluşturulan ifadelere sayı denir.

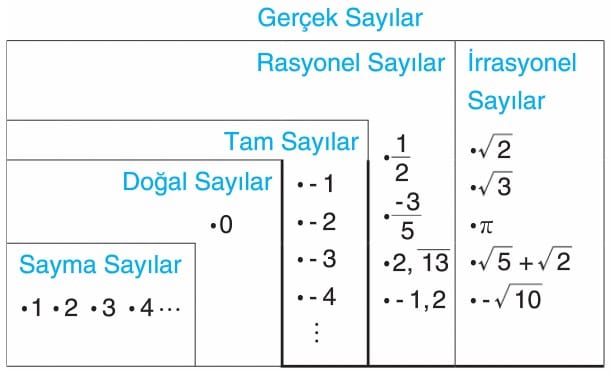
Sayı Kümeleri

1. Doğal Sayılar
N = {0, 1, 2, 3, …} kümesinin her bir elemanına doğal sayı denir.

2. Sayma Sayıları
N⁺ = {1, 2, 3, 4, …} kümesinin her bir elemanına sayma sayısı denir.

3. Tam Sayılar
Z = {…, -3, -2, -1, 0, 1, 2, 3, …} kümesinin her bir elemanına tam sayı denir.
Z⁺ = {1, 2, 3, …} kümesinin elemanlarına pozitif tam sayılar denir.
Z^– = {…, -3, -2, -1} kümesinin elemanlarına negatif tam sayılar denir.

Not: Sıfır tam sayıdır ancak pozitif veya negatif değildir.

4. Rasyonel Sayılar

a, b ∈ Z, b ≠ 0 olmak üzere, a/b şeklinde yazılabilen sayılara rasyonel sayılar denir ve Q ile gösterilir.
Q = {a/b; a, b ∈ Z, b ≠ 0}

Not: Her tam sayı aynı zamanda rasyonel sayıdır.

5. İrrasyonel Sayılar
Rasyonel olmayan sayılara irrasyonel sayılar denir. Q’ ile gösterilir.

6. Gerçek (Reel) Sayılar
Rasyonel sayılar kümesi ile İrrasyonel sayılar kümesinin birleşiminden oluşan kümeye gerçek sayılar denir ve R ile gösterilir.

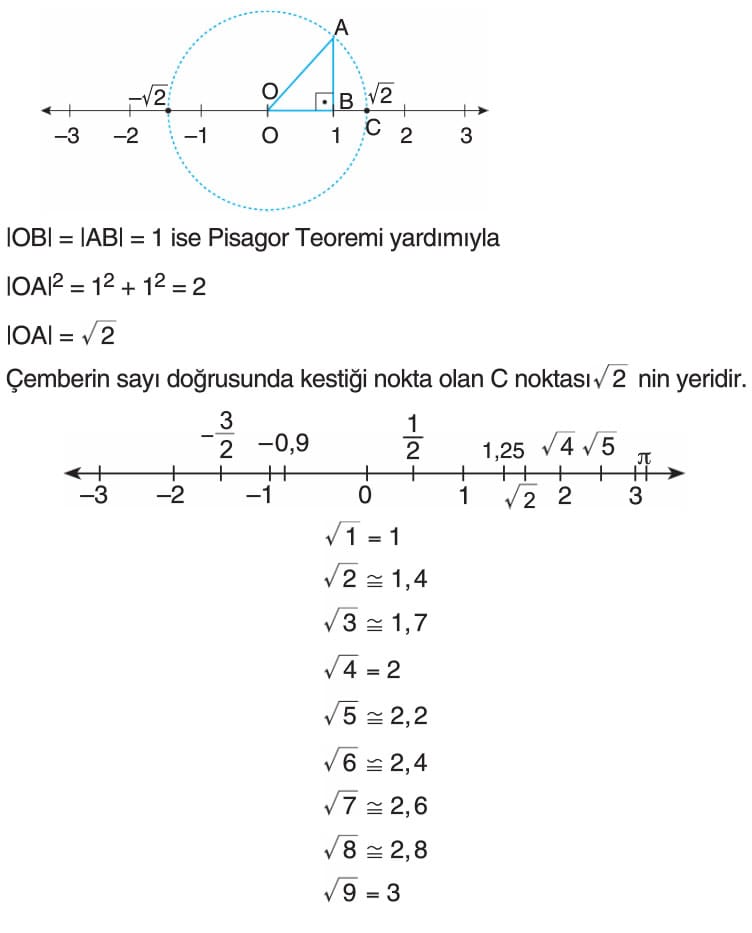
Sayı Doğrusu: Bir sayı doğrusu sonsuz noktanın birleşiminden oluşur ve her nokta bir gerçek sayıya karşılık gelir. Sayı doğrusu gerçek sayıların geometrik gösterimidir.

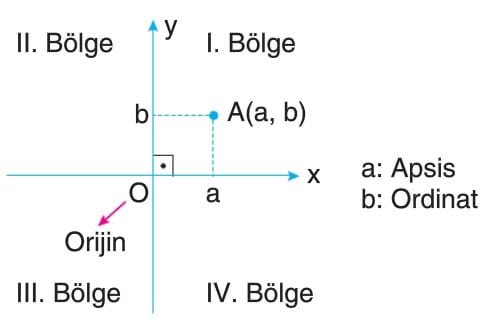
Koordinat Düzlemi

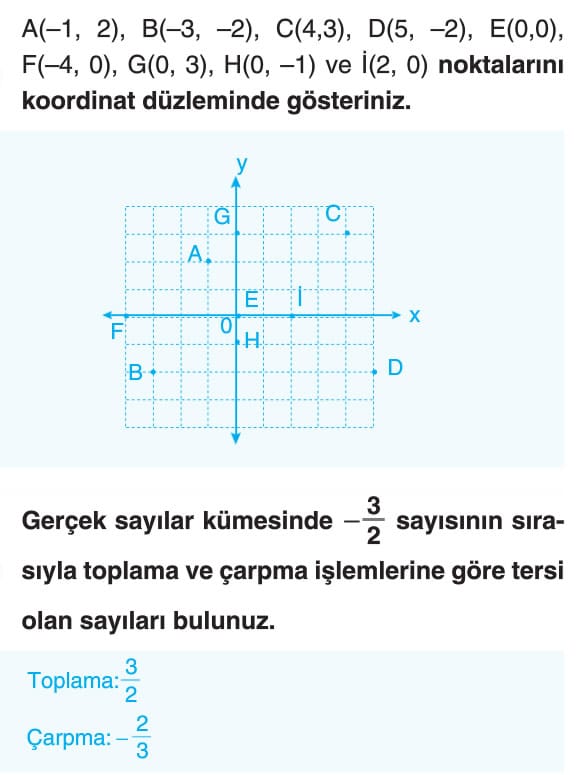
İki tane gerçek sayı doğrusunun 0 (sıfır) noktasında birbirine dik olacak şekilde kesiştirilmesiyle elde edilen düzleme koordinat düzlemi (analitik düzlem) denir. Reel sayılar kümesinin elemanlarıyla gösterilen her sıralı ikili, analitik düzlemde bir nokta belirtir.

Gerçek Sayılar Kümesinde Toplama ve Çarpma işleminin Özellikleri

Toplama İşleminin Özellikleri

1. Kapalılık özelliği: Her a, b ∈ R için a + b ∈ R dir.
9 ve 3 gerçek sayılardır ve 9 + 3 = 12 de bir gerçek sayıdır.

2. Değişme özelliği: Her a, b ∈ R için a + b = b + a dır.
9 + 3 = 3 + 9

3. Birleşme özelliği: Her a, b, c ∈ R için a + (b + c) = (a + b) + c dir.
9 + (3 + 5) = (9 + 3) + 5

4. Etkisiz (Birim) Eleman Özelliği: Her a ∈ R için a + 0 = 0 + a = a ise “0” toplama işleminin etkisiz (birim) elemanıdır.
9 + 0 = 0 + 9 = 9

5. Ters Eleman özelliği: Her a ∈ R için a + (-a) =(-a) + a = 0 olduğu için a nın toplama işlemine göre tersi -a dır.
9 + (-9) = (-9) + 9= 0

Çarpma İşleminin Özellikleri

1. Kapalılık özelliği: Her a, b ∈ R için a . b ∈ R dir.
9 ve 3 gerçek sayılardır ve 9 . 3 = 27 de bir gerçek sayıdır.

2. Değişme özelliği: Her a, b ∈ R için a . b = b . a dır.
9 . 3 = 3 . 9

3. Birleşme özelliği: Her a, b, c ∈ R için a . (b . c) = (a . b) . c dir.
9 . (3 . 5) = (9 . 3) . 5

4. Etkisiz (Birim) Eleman Özelliği: Her a ∈ R için a . 1 = 1 . a = a ise “1” çarpma işleminin etkisiz (birim) elemanıdır.
9 . 1 = 1 . 9 = 9

5. Ters Eleman Özelliği: Her a ∈ R için ve a ≠ 0 için a . 1/a = 1/a . a = 1 ise a nın çarpma işlemine göre tersi 1/a dır. 0 sayısının çarpma işlemine göre tersi yoktur.
9 . 1/9 = 1/9 . 9 = 1

6. Yutan Eleman özelliği: Her a ∈ R için a . 0 = 0 . a  = 0 ise çarpma işleminin yutan elemanı “0” dır.
9 . 0 = 0 . 9 = 0

7. Çarpma işleminin Toplama İşlemi Üzerine Dağılma Özelliği: Her a, b, c ∈ R için
a . (b + c) = a . b + a . c ve
(a + b) . c = a . c + b . c dir.
Bu özelliğe çarpma işleminin toplama işlemi üzerinde soldan ve sağdan dağılma özelliği denir.

Örneğin; 9 . (3 + 5) = 9 . 3 + 9 . 5
9 . 8 = 27 + 45
72 = 72

(9 + 3) . 5 =9 . 5 + 3 . 5
12 . 5 = 45 + 15
60 = 60

Sayı Kümeleri Arasındaki İlişki Soruları ve Çözümleri

Çözümlü Test Soruları 

Soru 1:

Aşağıdaki sayı kümelerinden hangisi diğerlerini kapsar?
A) Doğal sayılar
B) Tam sayılar
C) Rasyonel sayılar
D) İrrasyonel sayılar

Çözüm:
Rasyonel sayılar kümesi, doğal sayılar ve tam sayılar kümelerini kapsar.
Cevap: C

---

Soru 2:

√2 sayısı için aşağıdakilerden hangisi doğrudur?
A) Rasyonel sayıdır
B) Tam sayıdır
C) İrrasyonel sayıdır
D) Doğal sayıdır

Çözüm:
√2 virgülden sonra sonsuza kadar devam eden ve tekrar etmeyen bir sayı olduğu için irrasyonel sayıdır.
Cevap: C

---

Soru 3:

A = {x | x ∈ Z ve -3 ≤ x < 2} kümesinin eleman sayısı kaçtır?
A) 4
B) 5
C) 6
D) 7

Çözüm:
Kümedeki tam sayılar: -3, -2, -1, 0, 1 → 5 eleman
Cevap: B

---

Soru 4:

Aşağıdakilerden hangisi hem rasyonel hem de tam sayıdır?
A) 0,5
B) -4
C) √9
D) π

Çözüm:

• -4 tam sayıdır.

• √9 = 3 hem tam sayı hem de rasyonel sayıdır.
  Cevap: C

---

Soru 5:

Q ∩ I = ? (Q: Rasyonel sayılar, I: İrrasyonel sayılar)
A) Q
B) I
C) ∅ (Boş küme)
D) R

Çözüm:
Rasyonel ve irrasyonel sayıların kesişimi boş kümedir, çünkü bir sayı aynı anda hem rasyonel hem de irrasyonel olamaz.
Cevap: C