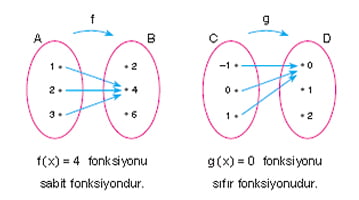
Sabit fonksiyon nedir?
f : A → B ve c ∈ B olsun. ∀x ∈ A için f(x) = c ise f fonksiyonuna sabit fonksiyon denir.
∀x ∈ A için f(x) = 0 ise f fonksiyonuna sıfır fonksiyonu denir. Sıfır fonksiyonu da özel bir sabit fonksiyondur.
Tanımlı olduğu bölgede f (x) = ax + b / cx + d sabit fonksiyon ise a / c = b / d dir.
Sabit Fonksiyon ve Sıfır Fonksiyonu Çözümlü Sorular
Çözümlü Örnek Test Soruları
1. Aşağıdaki fonksiyonlardan hangisi sabit fonksiyondur?
A) f(x) = 3x + 5
B) f(x) = x² – 4
C) f(x) = 7
D) f(x) = 2x – 1
Çözüm:
Sabit fonksiyon, tüm x değerleri için aynı sabit değeri veren fonksiyondur. Yani fonksiyonun içinde değişken (x) bulunmaz.
f(x) = 7 fonksiyonu her x değeri için 7 sonucunu verir, yani sabit fonksiyondur.
Doğru cevap: C
2. Aşağıdaki ifadelerden hangisi sıfır fonksiyonunu tanımlar?
A) f(x) = 0 fonksiyonu tüm x değerleri için 0 değerini alır.
B) f(x) = x fonksiyonu sıfır fonksiyonudur.
C) Sıfır fonksiyonunda her x için farklı değerler alınır.
D) Sıfır fonksiyonu yalnızca negatif sayılar için tanımlıdır.
Çözüm:
Sıfır fonksiyonu, tüm x değerleri için sonuç olarak sıfır veren fonksiyondur. Yani f(x) = 0 fonksiyonu her zaman sıfır değerini alır.
Doğru cevap: A
3. Aşağıdakilerden hangisi sabit fonksiyonun genel gösterimidir?
A) f(x) = mx + b
B) f(x) = c
C) f(x) = ax² + bx + c
D) f(x) = x³ – x
Çözüm:
Sabit fonksiyonun genel gösterimi f(x) = c şeklindedir. Burada c bir sabit sayıdır ve x değişse bile fonksiyonun değeri değişmez.
Doğru cevap: B
4. f(x) = 0 fonksiyonu hangi fonksiyon türüne örnektir?
A) Doğrusal fonksiyon
B) Sabit fonksiyon
C) Sıfır fonksiyonu
D) Hepsi
Çözüm:
Sıfır fonksiyonu, her x için 0 değerini veren bir fonksiyondur, yani f(x) = 0’dır. Aynı zamanda tüm sabit fonksiyonlar doğrusal fonksiyonlardır.
Bu nedenle f(x) = 0 fonksiyonu hem sabit hem doğrusal hem de sıfır fonksiyonudur.
Doğru cevap: D
5. Aşağıdakilerden hangisi sabit fonksiyonun grafiği hakkında doğru bir ifadedir?
A) x eksenini kestiği nokta fonksiyonun sabit değeridir.
B) Yatay bir doğru şeklindedir.
C) Orijinden geçer ve sabit bir eğime sahiptir.
D) Grafiği bir parabol oluşturur.
Çözüm:
Sabit fonksiyonların grafiği y = c biçiminde yatay bir doğrudur. Yani x eksenine paralel bir doğru şeklindedir.
Doğru cevap: B