Rasyonel Sayılarla İşlemler 7. Sınıf Matematik Ders Notu
Rasyonel sayılar, bir tam sayının başka bir tam sayıya bölünmesiyle oluşan sayılardır. Bu sayılarla toplama, çıkarma, çarpma ve bölme işlemleri, özellikle oranlar, kesirler ve paylaşım problemlerinde kullanılır. Rasyonel sayılarla çalışmak, günlük yaşamda oranlama ve hesaplamalar yaparken sıkça karşımıza çıkar. Bu ders notunda, rasyonel sayılarla işlemler üzerine paragraflı problemler çözecek ve bu kavramları pekiştireceksiniz.
Rasyonel Sayılar ve Rasyonel Sayılarla İşlemler Testleri
RASYONEL SAYILARLA TOPLAMA VE ÇIKARMA İŞLEMİ
İki rasyonel sayı toplanırken paydalar eşit değilse eşitlenir. Daha sonra paylar toplanır sonucun payına yazılır. Eşitlenen payda sonucun paydası aynen sonuca yazılır.
Uyarı: Birden fazla rasyonel sayı toplanırken önce aynı işaretli sayılar toplanır. Daha sonra ters işaretli sayılar toplanır.
Uyarı
- Tam sayılı kesirler toplanırken tam sayılar toplanıp tam sayı olarak; kesirler toplanıp kesir olarak yazılır.
- Tam sayılı kesirler toplanırken tam sayılı kesir bileşik kesre çevrilerek de toplanabilir.


Uyarı: Paydaları eşit aynı işaretli iki rasyonel sayı toplanırken ortak işaret sonuca yazılır. Ters işaretli iki sayı toplanırken mutlak değeri büyük olan paydan; mutlak değeri küçük olan pay çıkarılır, mutlak değeri büyük olan sayının işareti sonuca yazılır.

Uyarı: Doğal sayılarda ve tam sayılarda toplama-çıkarma işlemlerinde olduğu gibi rasyonel sayılarda da önce parantez içindeki işlemler yapılır. Ancak parantez kaldırıldığında paydaları ortak rasyonel sayılar varsa onlara işlem önceliği tanınabilir.



Uyarı: Rasyonel sayılarda çıkarma işleminin değişme, birleşme, etkisiz eleman ve ters eleman özellikleri yoktur.
RASYONEL SAYILARLA ÇARPMA VE BÖLME İŞLEMLERİ
Rasyonel Sayılarla Çarpma İşlemi
Uyarı:
- İki rasyonel sayı çarpılırken paylar çarpılarak paya, paydalar çarpılarak paydaya yazılır.
- Rasyonel sayılar, çarpılırken tam sayılı kesir varsa bileşik kesre çevrilir.
Rasyonel Sayıların Pozitif Tam Sayı Kuvvetleri
Uyarı: Rasyonel sayıların pozitif tam sayı kuvvetini hesaplama tam sayıların kuvvetini hesaplama ile aynıdır.
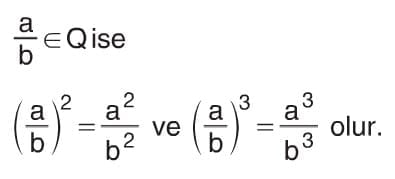
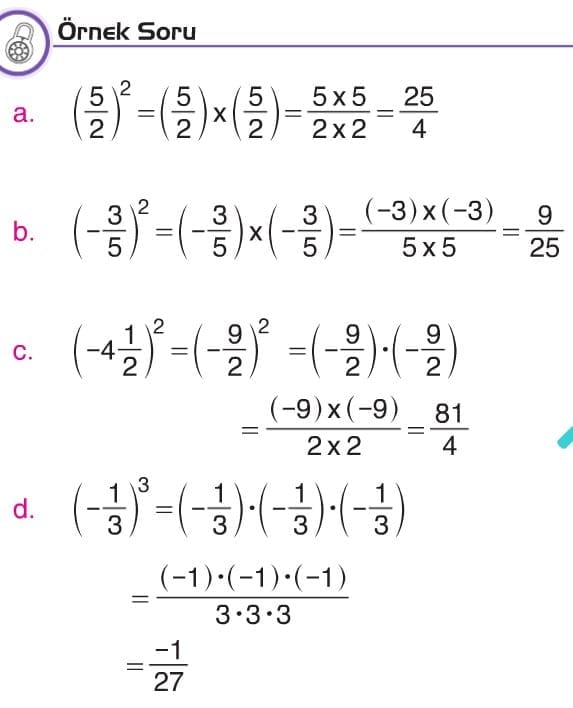
Çarpma işleminin Özellikleri






6. Çarpma İşleminin Toplama ve Çıkarma İşlemi Üzerine Dağılma Özelliği
Çarpma işleminin toplama – çıkarma işlemi üzerindeki dağılma özelliği kullanılırken parantezin dışındaki sayı, parantezin içindeki her sayı ile çarpılır ve bulunan sonuçlar toplanır ya da çıkarılır.
a, b, c rasyonel sayıları içi
a . (b + c) = a . b + a . c
a . (b – c) = a . b – a . c dir.

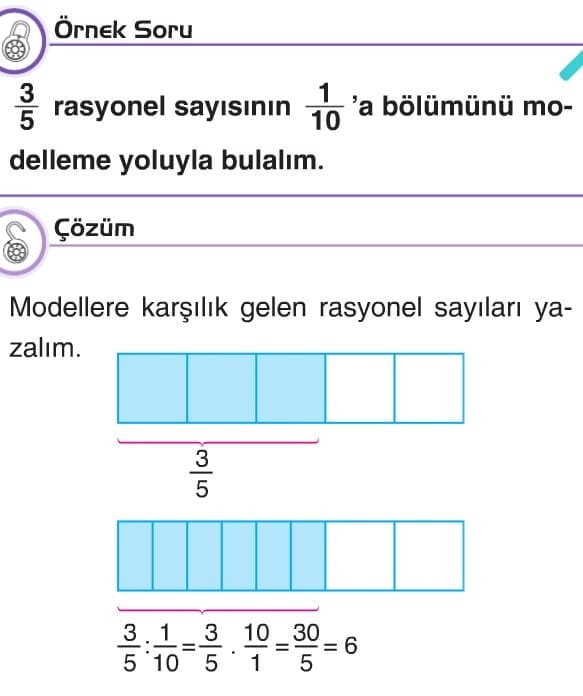
Rasyonel Sayılarla Bölme İşlemi
Uyarı: İki rasyonel sayıyı bölerken birincisi aynen yazılır, diğeri ters çevrilerek çarpılır.
Sıfırın Bölme İşlemine Etkisi
Sıfırın sıfırdan farklı bir sayının bölümü sıfırdır.


(+1) ve (-1)’in Bölme İşlemine Etkisi



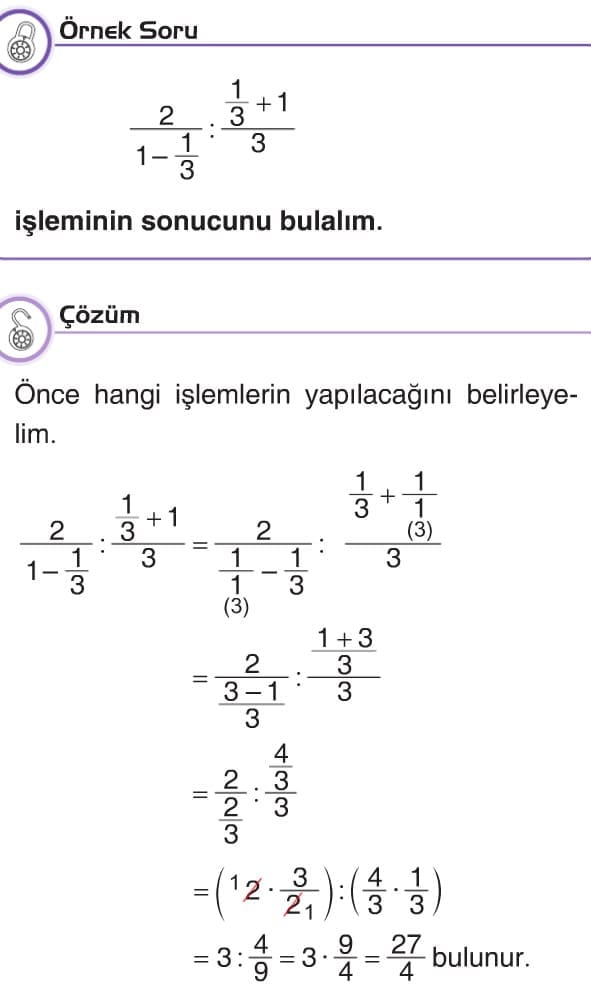
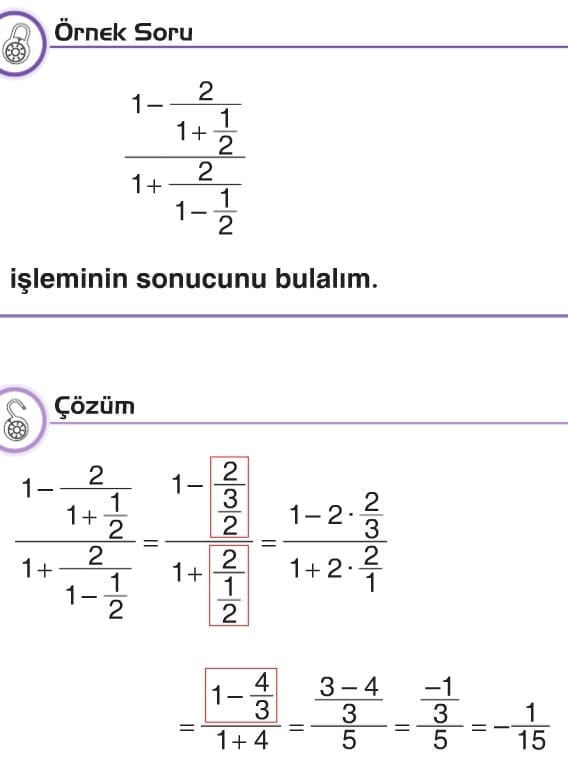
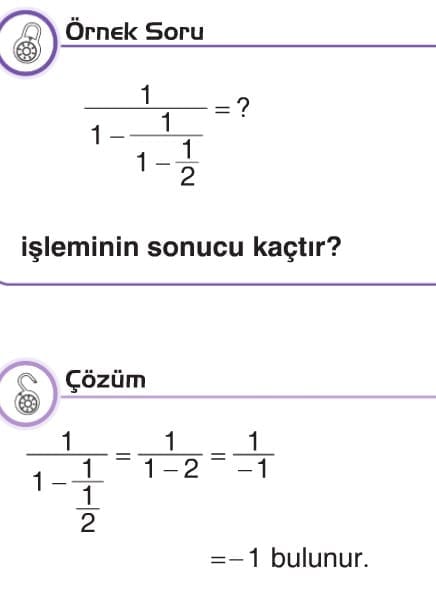
ÇOK ADIMLI İŞLEMLER VE PROBLEMLER
Bilgi Kutusu:
- Eğer işlemde büyük kesir çizgisi varsa büyük kesir çizgisinin altındaki ve üstündeki işlemler yapılır.
- İç içe parantezli işlemlerde en içtekinden en dışa doğru parantezli işlemler yapılır.
- Diğer işlemler yapılırken önce çarpma ve bölme, sonra toplama ve çıkarma işlemleri yapılır.
Rasyonel Sayılarla Problemler
Çözümlü Örnek Test Soruları
Soru 1:
Bir tarla sahibi, tarlasının 3/7’sine buğday, 2/7’sine arpa ekmiştir. Geri kalan kısma ise sebze ekmiştir. Eğer sebze ekilen kısım 60 dönümse, tarla sahibinin toplam tarlası kaç dönümdür?
A) 100 dönüm
B) 120 dönüm
C) 140 dönüm
D) 150 dönüm
Çözüm:
Tarla sahibinin tarlasının 3/7’sine buğday, 2/7’sine arpa ekilmiştir. Geriye kalan kısım sebze ekilen kısımdır ve bu 60 dönümdür. Bu durumda sebze ekili alan, toplam tarlanın:
1 – 3/7 – 2/7 = 2/7 oranında.
Bu bilgiye göre toplam tarlayı x ile gösterelim:
2/7x = 60
x = 60 x 7/2 = 210 dönüm.
Tarla sahibinin toplam tarlası 210 dönümdür.
Doğru cevap: C) 210 dönüm
Soru 2:
Bir otobüs, yolculuğun 4/9’luk kısmını tamamlamış ve kalan 5/9’luk kısmı da yakıt bitmeden tamamlamayı planlamaktadır. Eğer yolculuğun tamamı 180 kilometre ise, otobüsün kalan kaç kilometrelik yolu vardır?
A) 80 km
B) 90 km
C) 100 km
D) 110 km
Çözüm:
Yolculuğun tamamı 180 kilometredir. Otobüs, bu yolun 4/9’luk kısmını tamamlamıştır, bu yüzden kalan 5/9’luk kısmı hesaplamamız gerekir:
5/9 x 180 = 100 kilometre.
Otobüsün kalan yolu 100 kilometredir.
Doğru cevap: C) 100 km
Soru 3:
Bir marangoz, elindeki tahtaların 2/5’ini masa yapmak için kullanmış, 1/3’ünü ise dolap yapımında harcamıştır. Geri kalan 12 metrekare tahta ise başka bir projede kullanılmak üzere saklanmıştır. Marangozun başlangıçta kaç metrekare tahtası vardı?
A) 30 m²
B) 36 m²
C) 40 m²
D) 45 m²
Çözüm:
Başlangıçtaki toplam tahta miktarını x ile gösterelim. Marangoz tahtaların 2/5’ini masa yapımında, 1/3’ünü ise dolap yapımında kullanmıştır. Geriye kalan tahta ise 12 metrekaredir:
1 – 2/5 – 1/3 = 4/15’lik kısmı tahta olarak saklanmıştır.
4/15x = 12 olduğuna göre:
x = 12 x 15/4 = 45 m².
Marangozun başlangıçta 45 metrekare tahtası vardı.
Doğru cevap: D) 45 m²
Soru 4:
Bir havuzun 2/3’ü doludur. Havuzun geri kalanına su doldurulmaya başlanmış ve 1/4’ü doldurulmuştur. Bu işlemden sonra havuzun 30 metreküpü boş kaldığına göre, havuzun toplam kapasitesi kaç metreküptür?
A) 120 m³
B) 150 m³
C) 180 m³
D) 200 m³
Çözüm:
Havuzun 2/3’ü doludur ve 1/3’ü boş kalmıştır. Bu boş kısmın da 1/4’ü doldurulduktan sonra 30 metreküp su boşta kalmıştır. Başlangıçtaki toplam havuz kapasitesini x ile gösterelim:
Boş kısmın 1/4’ü doldurulmuş ve 3/4’ü boş kalmıştır.
3/4 x 1/3x = 30 olduğuna göre:
1/4x = 30
x = 120 m³.
Havuzun toplam kapasitesi 120 metreküptür.
Doğru cevap: A) 120 m³
Soru 5:
Bir market sahibi, aldığı ürünlerin 3/4’ünü sattıktan sonra geri kalan ürünlerin 1/3’ünü indirimli olarak satmıştır. İndirimli olarak satılan ürünler 20 taneyse, market sahibi başlangıçta kaç ürün almıştır?
A) 60
B) 80
C) 90
D) 120
Çözüm:
Başlangıçta alınan ürün sayısını x ile gösterelim. Market sahibi ürünlerin 3/4’ünü sattıktan sonra 1/4’ü kalmıştır. Bu kalan ürünlerin de 1/3’ü indirimli satılmıştır:
1/3 x 1/4x = 20 olduğuna göre:
1/12x = 20
x = 20 x 12 = 240 ürün.
Market sahibi başlangıçta 240 ürün almıştır.
Doğru cevap: D) 240