Dik Prizmalar

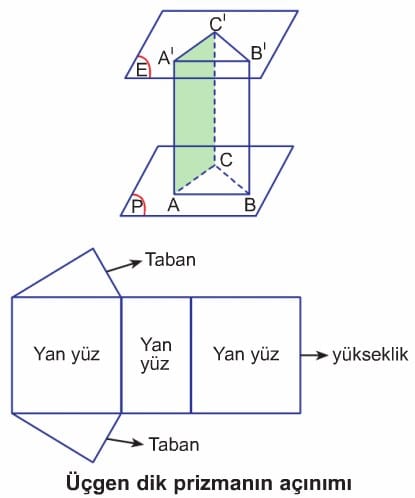
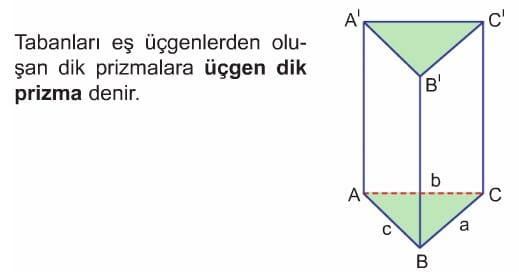
E // P olsun. P ve E düzlemleri içinde yer alan eş iki çokgenin köşeleri karşılıklı olarak birleştirilirse elde edilen cisme prizma denir,

• Çokgenlerin her birine prizmanın tabanları,
• Çokgenlerin kenarlarına taban ayrıtları,
• Çokgenlerin köşelerine prizmanın köşeleri,
• Taralı dikdörtgene prizmanın yanal yüzü,
• İki taban arasındaki dik uzaklığa ise prizmanın yüksekliği denir.

Özellikleri:

• Yan yüzleri tabanlara diktir.
• Yan yüzleri dikdörtgensel bölgedir.
• Tabanları eş çokgensel bölgeler olup birbirine paraleldir.
• Köşe sayısı taban çokgeninin kenar sayısının 2 katıdır.
• Ayrıt sayısı taban çokgeninin kenar sayısının 3 katıdır.
• Taban ayrıtlarının sayısı yaz

Özetle

n kenarlı bir çokgen olan dik prizmanın;
1) 2.n tane köşesi vardır.
2) n+2 tane yüzü vardır.
3) 3.n tane ayrıtı vardır.
4) 2 tane tabanı vardır.

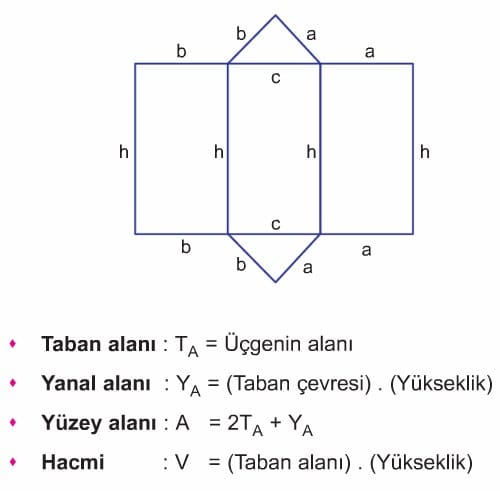
Prizmanın Alanı ve Hacmi

Bütün prizmaların alan ve hacimleri aynı şekilde hesaplanır.

Hacim: V = (Taban alanı) . (Yükseklik)
Yanal alan: Y_A = (Taban çevresi) . (Yükseklik)
Yüzey alanı: A = (Yanal alan) + 2.(Taban alanı)

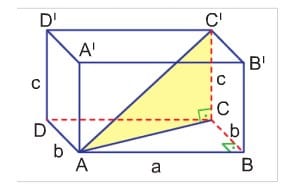
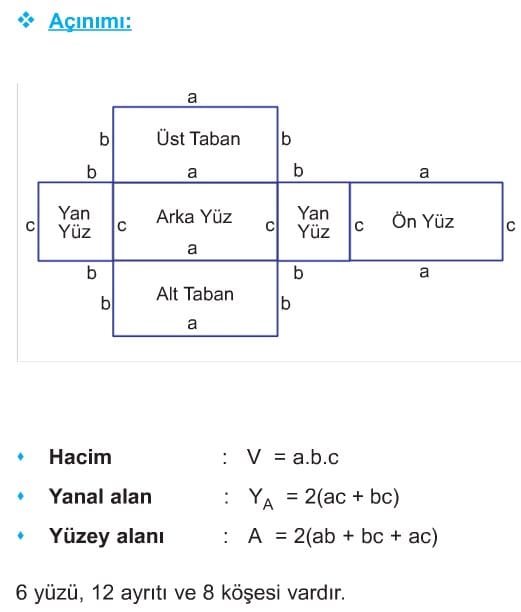
DİKDÖRTGENLER PRİZMASI

Bütün yüzleri dikdörtgen olan dik prizmaya dikdörtgenler prizması denir.

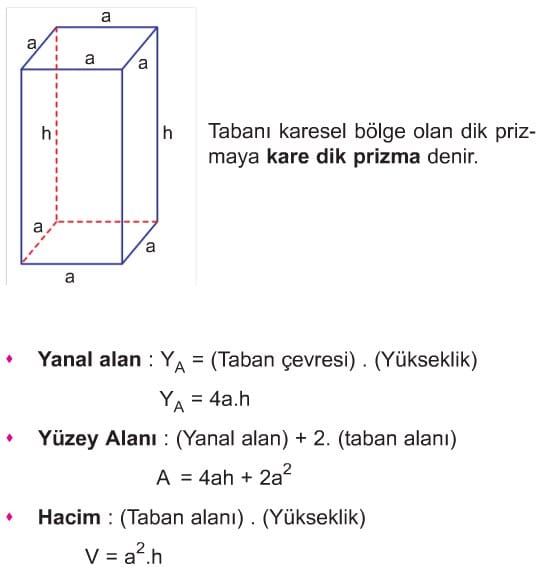
KARE DİK PRİZMA

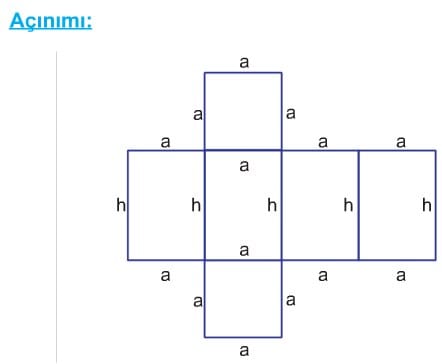
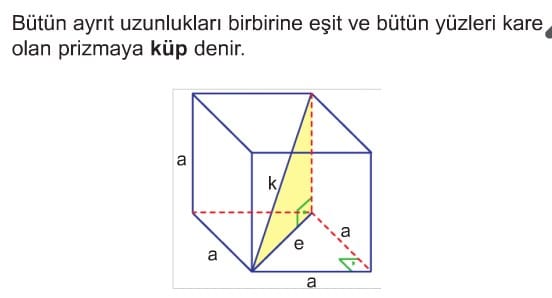
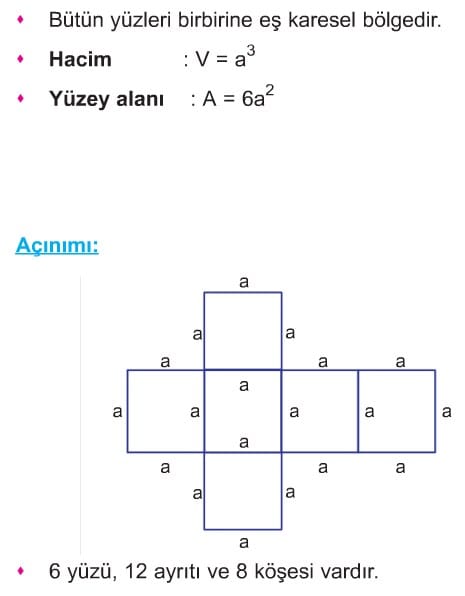
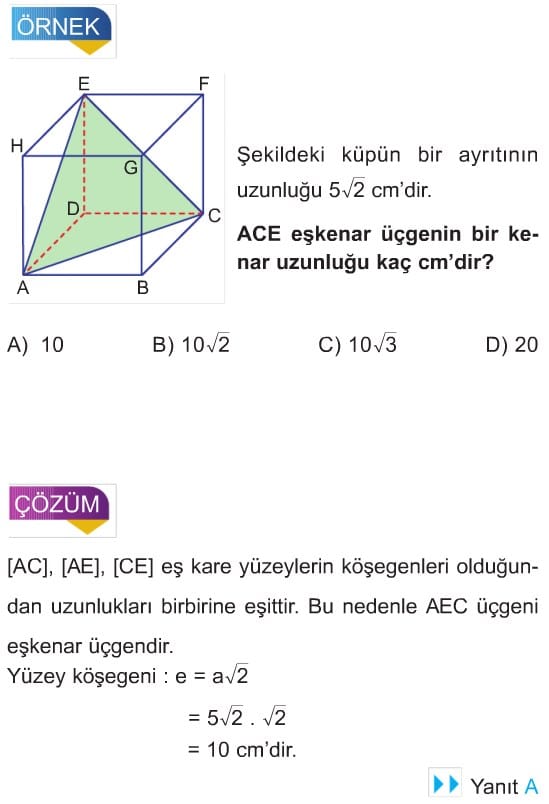
KÜP

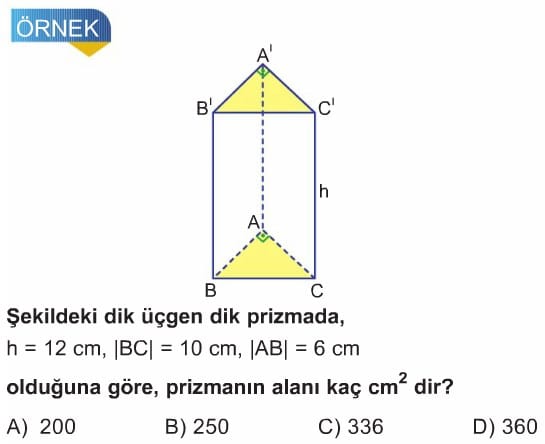
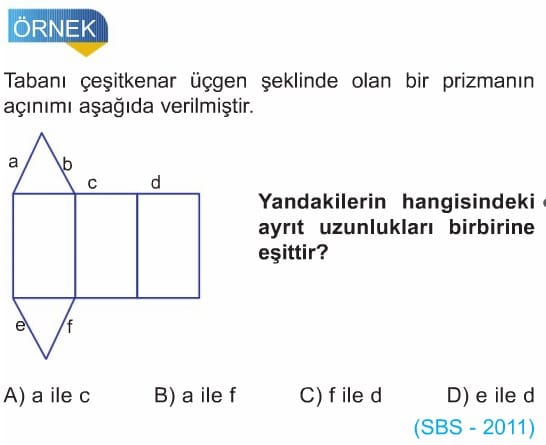
ÜÇGEN DİK PRİZMA

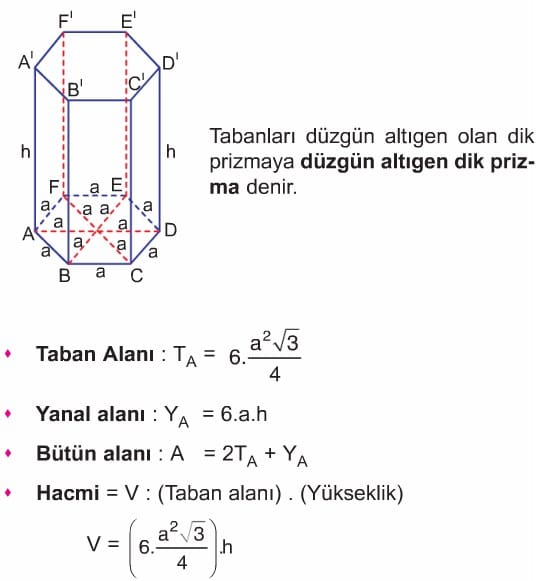
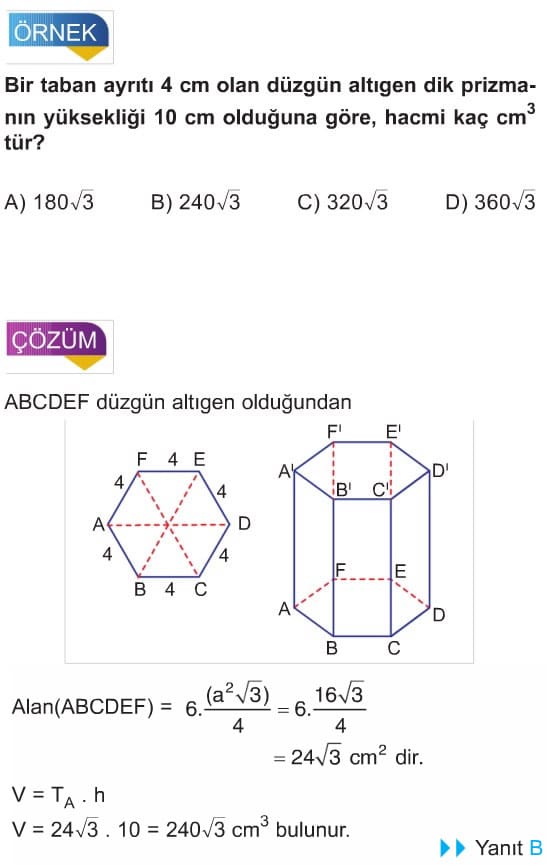
DÜZGÜN ALTIGEN DİK PRİZMA

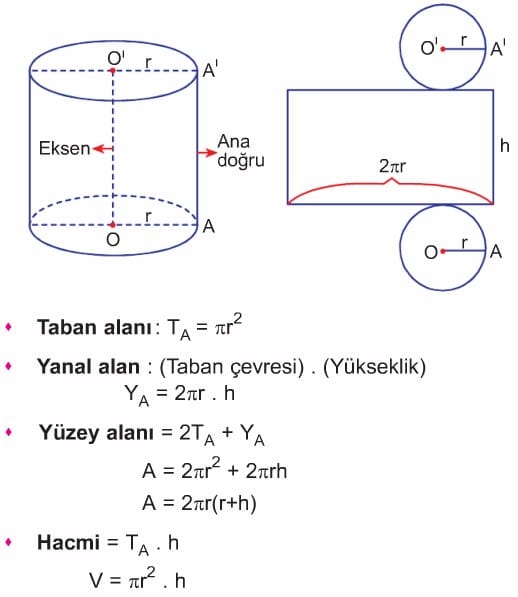
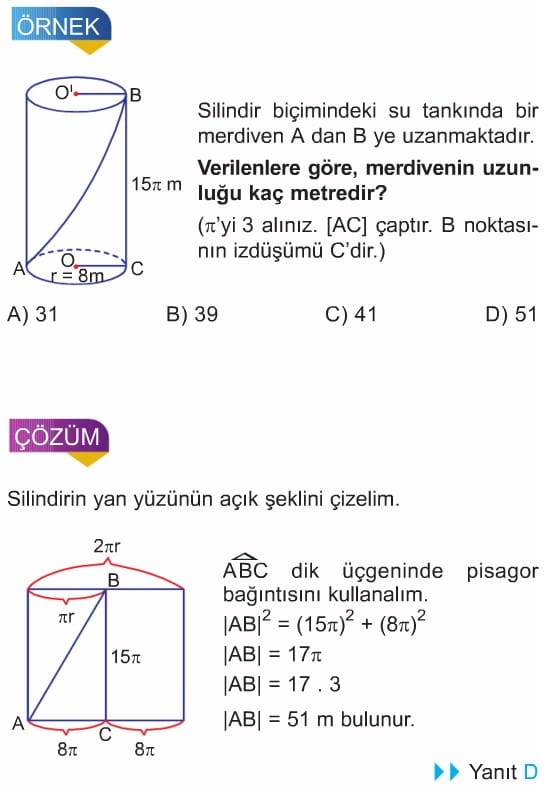
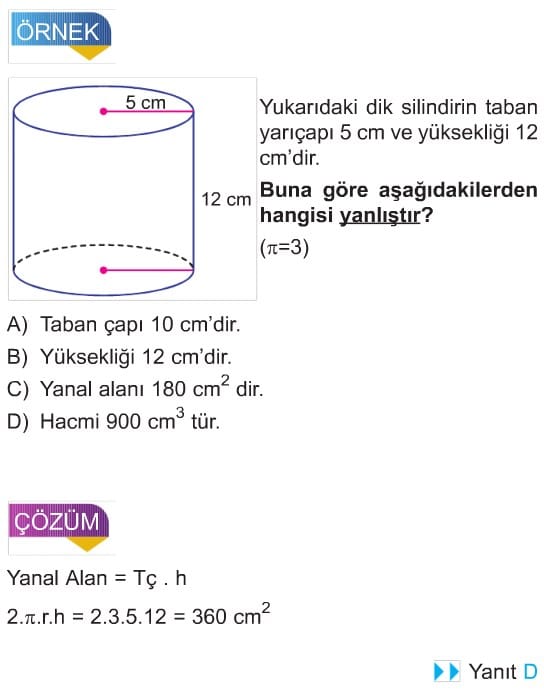
DİK SİLİNDİR

• Tabanı daire olan dik prizmaya silindir denir.
• Bir dikdörtgenin bir kenarı etrafında 360° döndürülmesiyle dik (dönel) silindir elde edilir. 180° döndürülmesiyle yarım silindir oluşur.
• Dikdörtgen hangi kenar etrafında döndürülürse o kenar yükseklik, diğer kenar taban dairesinin yarıçapı olur.