Pozitif tam sayıların çarpanları konusu, LGS matematik müfredatının önemli bir parçasıdır. Bu konuda, bir sayıyı tam bölen sayıları yani çarpanları öğreniriz. Çarpanlar konusunu anlamak, asal sayıları, EBOB-EKOK hesaplamalarını ve sayıların bölünebilme kurallarını anlamak açısından kritik öneme sahiptir. Bu konu ile sayıları daha iyi analiz etme yeteneği kazanır, problem çözme becerilerinizi geliştirirsiniz. Pozitif tam sayıların çarpanları, hem sayıların yapısını anlamaya yardımcı olur hem de ileride daha karmaşık matematiksel işlemler için temel oluşturur.
Lgs 8. Sınıf Pozitif Tam Sayıların Pozitif Tam Sayı Çarpanları Testleri
LGS 8. SINIF POZİTİF TAM SAYILARIN POZİTİF TAM SAYI ÇARPANLARI DERS NOTU
Pozitif tam sayılar iki tam sayının çarpımı şeklinde yazılabilir. Elde edilen çarpanların her birine pozitif tam sayının çarpanları denir.
Not: Pozitif tam sayıların çarpanlarını bulurken çarpan ağacı yönteminden faydalanabiliriz.
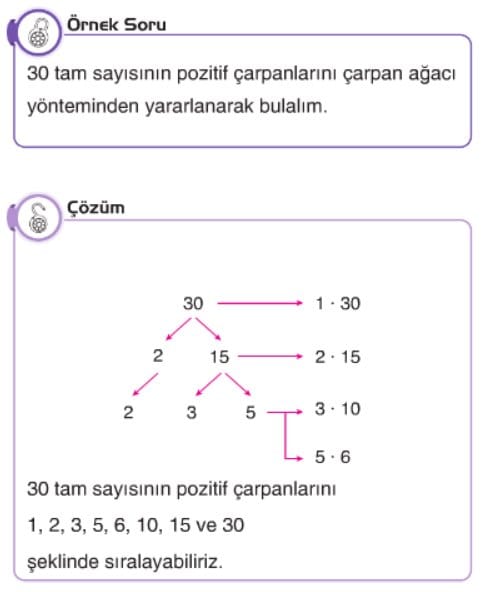
Not: 1 sayısından ve kendisinden başka böleni olmayan sayılara asal sayı denir. Asal sayılar 2, 3, 5, 7, şeklinde devam ederek gider. En küçük asal sayı 2 olup asal sayılar arasında çift sayı olan tek sayıdır.
Not: Pozitif tam sayıların asal çarpanlarını bulurken asal çarpanlar algoritmasından faydalanabiliriz.
Not: Pozitif tam sayılar üslü ifade veya üslü ifadelerin çarpımı şeklinde yazılabilir.
Aralarında Asal Sayılar
Pozitif Tam Sayıların Pozitif Tam Sayı Çarpanları Çözümlü Sorular
Soru 1: Bir Sayının Çarpanları
Verilen 36 sayısının kaç tane pozitif tam sayı çarpanı vardır?
Çözüm: Öncelikle 36 sayısını asal çarpanlarına ayıralım:
36 = 2² × 3²
Bir sayının çarpan sayısını bulmak için, asal çarpanların kuvvetlerinin her birine 1 ekleyip çarpıyoruz:
(2 + 1) × (2 + 1) = 3 × 3 = 9
Sonuç olarak, 36 sayısının 9 tane pozitif tam sayı çarpanı vardır.
Soru 2: Verilen Bir Aralıkta Çarpan Sayısı
Aşağıdaki sayılardan hangisinin çarpan sayısı 10’dan fazladır?
a) 30
b) 18
c) 24
d) 36
Çözüm: Her bir sayının çarpan sayısını bulmak için asal çarpanlarına ayıracağız ve formülü uygulayacağız.
- 30‘un asal çarpanları:
30 = 2¹ × 3¹ × 5¹
Çarpan sayısı: (1 + 1) × (1 + 1) × (1 + 1) = 2 × 2 × 2 = 8 - 18‘in asal çarpanları:
18 = 2¹ × 3²
Çarpan sayısı: (1 + 1) × (2 + 1) = 2 × 3 = 6 - 24‘ün asal çarpanları:
24 = 2³ × 3¹
Çarpan sayısı: (3 + 1) × (1 + 1) = 4 × 2 = 8 - 36‘nın asal çarpanları:
36 = 2² × 3²
Çarpan sayısı: (2 + 1) × (2 + 1) = 3 × 3 = 9
Bu sayılardan hiçbiri 10’dan fazla çarpana sahip değil. Yanıt olarak en yakın olan 36’dır ve 9 çarpanı vardır.
Soru 3: Çarpanlar Arasındaki Fark
48 sayısının pozitif tam sayı çarpanlarının kaç tanesi 8’in katıdır?
Çözüm: Önce 48 sayısının çarpanlarını bulalım. 48’in asal çarpanları:
48 = 2⁴ × 3¹
Çarpan sayısı: (4 + 1) × (1 + 1) = 5 × 2 = 10
48’in çarpanları: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
Şimdi, bu çarpanlardan 8’in katı olanları bulalım:
8, 16, 24, 48
8’in katı olan çarpanlar: 4 tanedir.
Soru 4: Çarpan Sayısı ve Ortak Bölenler
18 ve 24 sayılarının ortak pozitif tam sayı çarpanlarının sayısı kaçtır?
Çözüm: Öncelikle her iki sayının asal çarpanlarını bulalım:
- 18 = 2¹ × 3²
- 24 = 2³ × 3¹
İki sayının ortak çarpanlarını bulmak için her iki sayıdaki ortak asal çarpanların en küçük kuvvetlerini alacağız:
- Ortak çarpanlar: 2¹ × 3¹ = 6
Ortak bölenlerin çarpan sayısını bulmak için asal çarpanların kuvvetlerine 1 ekleyip çarparız:
- (1 + 1) × (1 + 1) = 2 × 2 = 4
Sonuç: 18 ve 24 sayılarının 4 ortak pozitif tam sayı çarpanı vardır.
