Gerçek Katsayılı Bir Polinomun Çarpanlara Ayrılması

• P(x) = Q(x) .R(x) ise Q(x) ve R(x) polinomlarına P(x) polinomunun çarpanları denir.
• Bir polinomu iki ya da daha çok polinomun çarpımı biçiminde yazma işlemine bu polinomu çarpanlarına ayırma işlemi denir.
• En az birinci dereceden iki polinomun çarpımı biçiminde yazılamayan ve sabit olmayan polinomlara indirgenmeyen polinom denir.
• Başkatsayısı 1 olan ve indirgenmeyen polinomlara asal polinom denir.

→ P(x) = x² + 1, Q(x) = 5x, R(x) = 3x + 2 indirgenemeyen polinomlardır.
→ P(x) = x + 4 , Q(x) = x – 1, R(x) = x – 3 asal polinomlardır.

Çarpanlara Ayırma Yöntemleri

1) Ortak çarpan Parantezine Alma

Bir polinomun ya da bir cebirsel ifadenin terimlerinde ortak çarpanlar varsa ortak çarpanların en küçük üstlerinin çarpımı, bu polinomun her teriminin ortak çarpanıdır. Şimdi örneklerle gösterelim.

Aşağıdaki ifadeleri çarpanlara ayıralım.

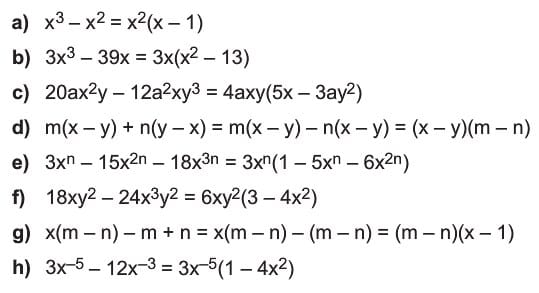
2) Gruplandırılarak Çarpanlara Ayırma

Verilen ifadenin her teriminde ortak çarpan yoksa ortak çarpanı olan terimler kendi aralarında gruplandırılarak ortak çarpan parantezine alınır.

Not:

3) Tam Kare Özdeşliği

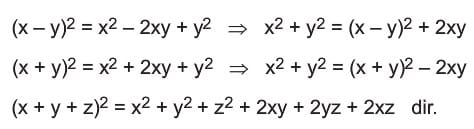
4) İki Kare Farkı Özdeşliği

İki terimin toplam ve farkının çarpımı ile elde edilen ifade, iki kare farkıdır.

x² – y² = (x – y).(x + y) ile gösterilir.

Aşağıdaki ifadeler iki kare farkı özdeşliğinden yararlanılarak çarpanlarına ayrılmıştır. İnceleyiniz.

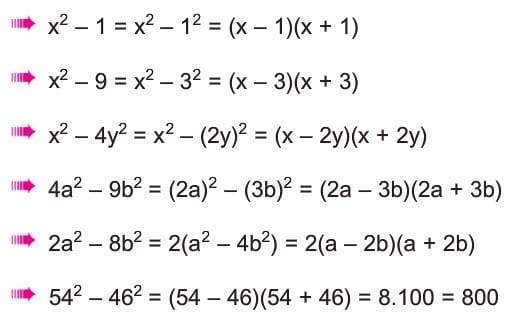
5) İki Terimin Toplam ve Farkının Küpü

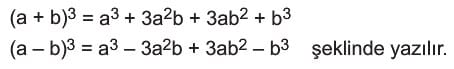
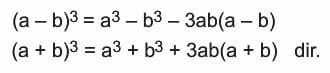
6) İki Küp Toplamı ve İki Küp Farkı

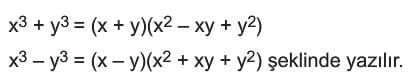
7) Bir Polinoma Terim Ekleyip çıkararak Çarpanlarına Ayırma

Bir polinoma terim ekleyip çıkararak çarpanlarına ayırmada, verilen polinomu iki kare farkına dönüştürebilecek uygun bir terim eklenir veya çıkarılır.

Aşağıdaki polinomları çarpanlarına ayıralım.

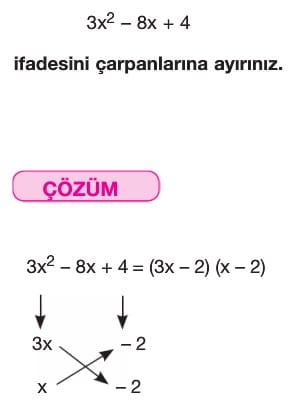
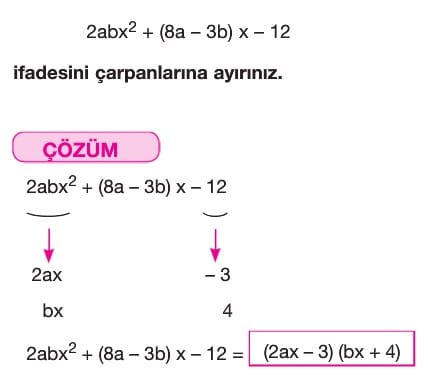
8) ax²+bx+c İfadesinin Çarpanlarına Ayrılması

9) Değişken Değiştirerek Çarpanlarına Ayırma

Değişken değiştirme yönteminde, verilen İfadedeki değişkenin ya da belli bir ifadenin yerine yeni bir değişken yazılarak verilen ifade sade hale getirilir. Sade hale gelmiş ifade çarpanlarına ayrılır.

NOT: Bir eşitlik, eşitlikte bulunan değişkenin her değeri için sağlanıyorsa bu eşitlik, bir ÖZDEŞLİKtir. Eşitlik değişkenin özel değeri ya da özel değerleri için sağlanıyorsa bu eşitlik bir DENKLEMdir.
(x – 2)2 = x2 – 4x + 4 eşitliği bir özdeşliktir.
x2 – 3x = 10 eşitliği bir denklemdir.

Polinomlarda Çarpanlara Ayırma – 10. Sınıf Çözümlü Test Soruları

Soru 1:
Aşağıdaki polinomu çarpanlarına ayırınız:
P(x) = x² – 9

A) (x + 3) . (x – 3)
B) (x + 9) . (x – 9)
C) (x – 3)²
D) (x + 3)²
E) x . (x – 9)

Çözüm:
Bu ifade iki kare farkıdır. İki kare farkı formülü şu şekildedir: a² – b² = (a + b) . (a – b)
Bu durumda a = x ve b = 3 olduğundan,
P(x) = (x + 3) . (x – 3) olur.

Cevap: A

Soru 2:
Aşağıdaki polinomu çarpanlarına ayırınız:
P(x) = x² + 5x + 6

A) (x + 2) . (x + 3)
B) (x – 2) . (x – 3)
C) (x + 6) . (x + 1)
D) (x + 3) . (x + 6)
E) (x – 1) . (x – 6)

Çözüm:
Verilen polinom iki çarpanın çarpımı şeklinde yazılabilir. Bu çarpanlar öyle seçilmelidir ki çarpımları sabit terimi, toplamları ise ortadaki katsayıyı versin. 6 sayısının çarpanları 2 ve 3 olduğundan,
P(x) = (x + 2) . (x + 3) olur.

Cevap: A

Soru 3:
Aşağıdaki polinomu çarpanlarına ayırınız:
P(x) = x² + 8x + 16

A) (x + 4) . (x + 4)
B) (x – 4) . (x + 4)
C) x . (x + 16)
D) x . (x + 8)
E) (x + 16) . (x + 1)

Çözüm:
Bu ifade tam kare üç terimlidir. Ortadaki terimin yarısının karesi, sabit terime eşittir. Bu nedenle,
P(x) = (x + 4) . (x + 4) şeklinde çarpanlarına ayrılır.

Cevap: A

Soru 4:
Aşağıdaki polinomu çarpanlarına ayırınız:
P(x) = 2x² + 8x

A) 2x . (x + 4)
B) x . (x + 4)
C) 2 . (x² + 4x)
D) 2x . (x – 4)
E) 2x . (x + 2)

Çözüm:
Bu ifade ortak çarpan parantezine alınabilir. 2x ortak çarpandır.
P(x) = 2x . (x + 4)

Cevap: A

Soru 5:
Aşağıdaki polinomu çarpanlarına ayırınız:
P(x) = x² – 4x + 4

A) (x – 2) . (x – 2)
B) (x + 2) . (x + 2)
C) x . (x + 4)
D) x . (x – 4)
E) (x – 4) . (x + 2)

Çözüm:
Bu ifade tam kare üç terimlidir. Ortadaki terimin yarısının karesi, sabit terime eşittir. Bu nedenle,
P(x) = (x – 2) . (x – 2)

Cevap: A