Polinomlarda Bölme ve Kalan Bulma 10. Sınıf
P(x) ve Q(x) polinomları verilsin. Q(x) ≠ 0 olmak üzere, P(x) polinomunun Q(x) polinomuna bölümü
Polinomlarda Bölme İşlemi Yapılırken
- Bölünen ve bölen polinomun terimleri azalan derecelerine göre yazılır.
- Bölünenin en büyük dereceli terimi, bölenin en büyük dereceli terimine bölünür.
- Bulunan bölüm bölenle çarpılır, elde edilen çarpım bölünenden çıkarılır.
- Kalanın derecesi, bölenin derecesinden küçük oluncaya kadar bölme işlemi aynı yöntemle devam eder.
Horner Metodu ile Bölme İşlemi
Horner metodu, bir P(x) polinomunun ax + b biçimindeki birinci dereceden bir polinoma bölünmesinden elde edilen bölüm ve kalanı bulmada kolaylık sağlar. Bu metodu bir örnekle açıklayalım.

P(x) Polinomunun x – a ile Bölümünden Kalanın Bulunması
P(x) polinomunun x – a ile bölünmesinden elde edilen kalan, P(x) polinomunda x yerine a yazılarak bulunan P(a) değeridir.
NOT: Polinomlarda bölme işlemini yapmadan kalanı bulmak için böleni sıfır yapan kökü polinomda yerine yazmalıyız.


P(x) Polinomunun (x – a).(x – b) İle Bölümünden Kalanın Bulunması


P(x) Polinomunun ax2+b İle Bölümünden Kalanın Bulunması


Polinomların Tam Sayı Sıfırları
Tam sayı, katsayılı ve başkatsayısı 1 olan polinomların tam sayı sıfırları varsa bu sıfırlar sabit terimin çarpanları arasındadır. Şimdi bir örneklerle gösterelim.

Polinomlarda Bölme ve Kalan Bulma Soruları ve Çözümleri
Çözümlü Örnek Test Soruları:
Soru 1:
Bir araştırma projesi kapsamında Ayşe, bir polinomun grafiğini incelemektedir. Verilen polinom P(x) = 2x³ – 3x² + x – 2 polinomunun x – 2 ile bölümünü ve kalanını hesaplayarak bu polinomun grafiğinin x = 2 noktasından geçip geçmediğini belirlemek istemektedir. Bu noktada grafiğin geçip geçmediğini belirleyebilmesi için hangi hesaplamayı yapması gerekmektedir? Ayşe’nin sorusunu çözün ve grafiğin bu noktadan geçip geçmediğini belirtin.
Çözüm:
Polinomun grafiği x = 2 noktasından geçiyorsa, P(2) = 0 olmalıdır. Şimdi P(2) hesaplayalım:
P(2) = 2(2)³ – 3(2)² + (2) – 2
P(2) = 2(8) – 3(4) + 2 – 2
P(2) = 16 – 12 + 2 – 2 = 4
P(2) = 4 olduğuna göre, polinomun grafiği x = 2 noktasından geçmez.
Cevap: Grafiğin x = 2 noktasından geçmesi için P(2) = 0 olmalıydı, ancak P(2) = 4 olduğundan grafiğin bu noktadan geçmediği sonucu çıkmaktadır.
Soru 2:
Bir öğretmen, öğrencilerine bir polinom sorusu soruyor: P(x) = x⁴ – 4x³ + 6x² – 4x + k polinomu, x – 1 ile tam bölünebildiğine göre k sabiti nedir? Öğretmenin sorusunu çözün ve k değerini bulun.
Çözüm:
Bir polinom, x – a ile tam bölünebiliyorsa, P(a) = 0 olmalıdır. Burada a = 1 olduğuna göre P(1) = 0 olmalıdır. Şimdi P(1)’i hesaplayarak k’yi bulalım:
P(1) = (1)⁴ – 4(1)³ + 6(1)² – 4(1) + k
P(1) = 1 – 4 + 6 – 4 + k
P(1) = -1 + k
Polinom x – 1 ile tam bölünebildiği için P(1) = 0 olmalıdır. Bu durumda:
-1 + k = 0
k = 1
Cevap: k = 1
Soru 3:
Bir mühendislik problemi için bir polinomun bölme işlemi yapılmaktadır. Verilen polinom P(x) = 5x⁵ – 3x³ + x² – 6x + 4, Q(x) = x – 2 ile bölünmek isteniyor. Bu bölme işleminde kalan nedir? Kalanı hesaplayın.
Çözüm:
Kalanı bulmak için, polinomu Q(x) = x – 2 ile böleceğiz. Bunun için x – 2 ifadesinde a = 2 olacaktır. Şimdi P(2)’yi hesaplayalım:
P(2) = 5(2)⁵ – 3(2)³ + (2)² – 6(2) + 4
P(2) = 5(32) – 3(8) + 4 – 12 + 4
P(2) = 160 – 24 + 4 – 12 + 4
P(2) = 132
Cevap: Kalan 132
Soru 4:
Bir fabrika, bir üretim modeline göre belirli bir polinomu analiz etmektedir. Polinom P(x) = 4x³ – 2x² + x + b, x – 3 ile bölündüğünde kalan 5 ise, b kaçtır? Fabrika üretim modelinin doğru sonuçlar verebilmesi için b’nin hangi değerde olduğunu bulun.
Çözüm:
Bir polinom x – a ile bölündüğünde, kalan P(a) ile bulunur. Burada a = 3 ve kalan 5 olduğuna göre, P(3) = 5 olmalıdır. Şimdi P(3)’ü hesaplayıp b’yi bulalım:
P(3) = 4(3)³ – 2(3)² + (3) + b
P(3) = 4(27) – 2(9) + 3 + b
P(3) = 108 – 18 + 3 + b
P(3) = 93 + b
Polinomun x – 3 ile bölümünden kalan 5 olduğuna göre:
93 + b = 5
b = 5 – 93
b = -88
Cevap: b = -88
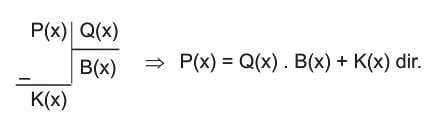
























sınav sorusu olsa keşke çok kolaylar.
PIRLANTA DÖVMESİ İSTEYEN…