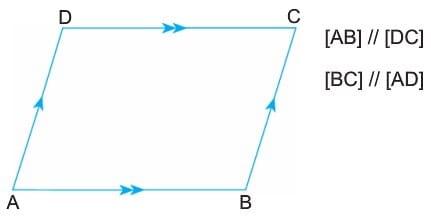
Karşılıklı kenarları paralel olan dörtgenlere paralelkenar denir.

Paralelkenarın Özellikleri

Özellik:

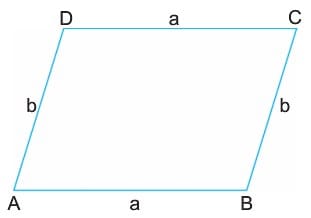
Paralelkenarda karşılıklı kenarların uzunlukları eşittir.
|AB|=|DC|=a, |AD|=|BC|=b

Özellik:

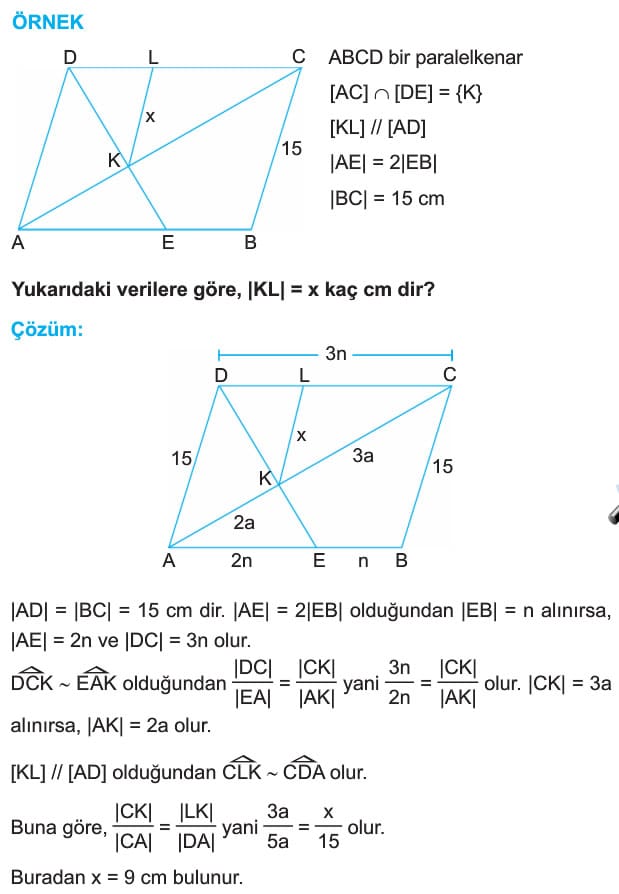
Çözümlü Sorular

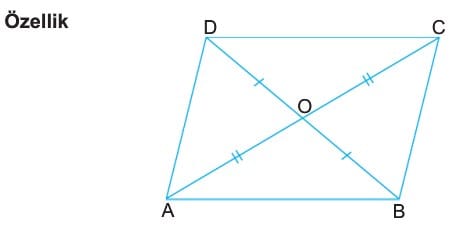
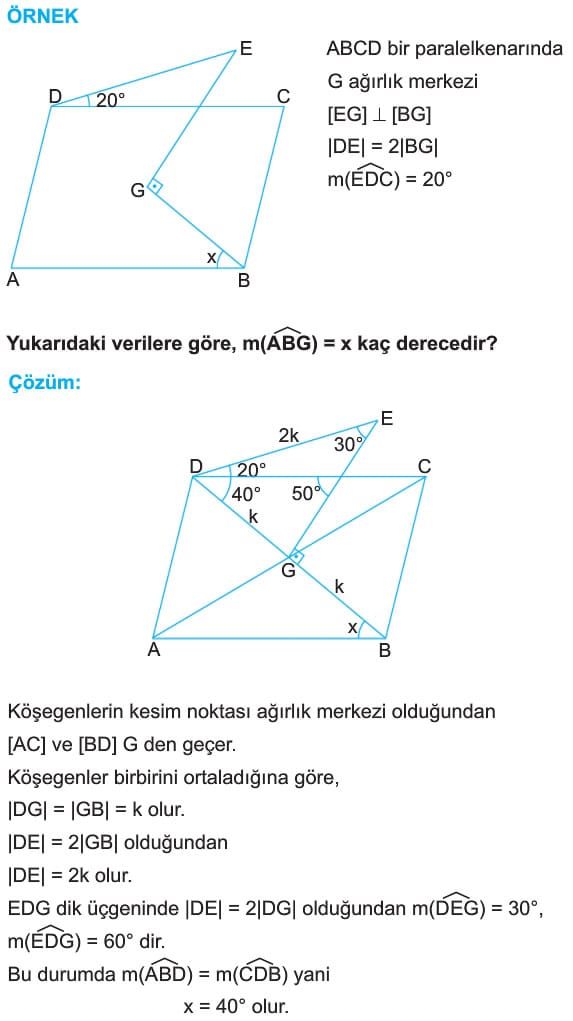
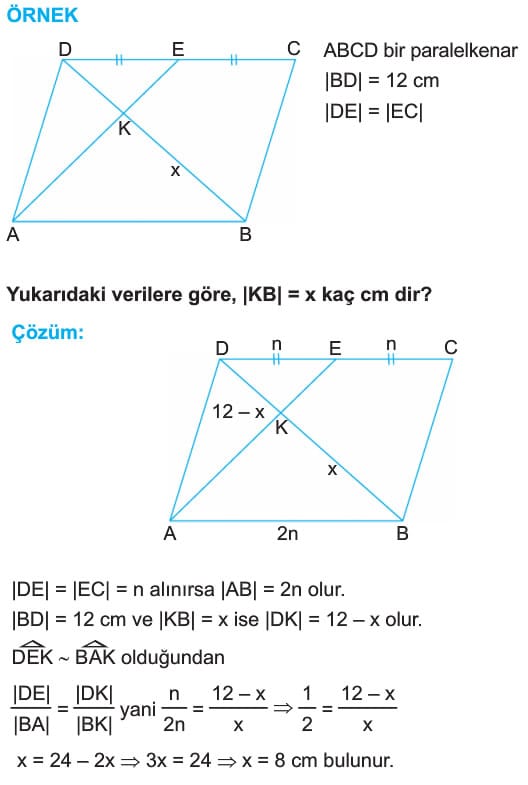
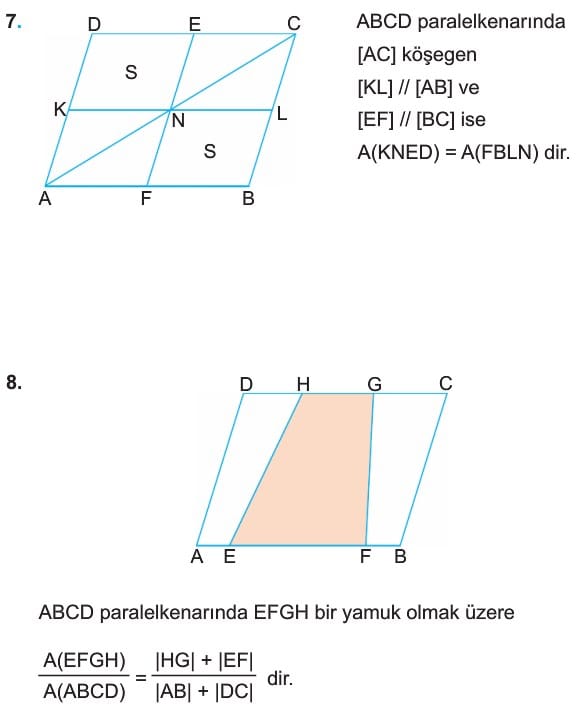
Paralelkenarlarda köşegenler birbirini ortalar. Buna göre, ABCD paralelkenarında
|AO| = |OC| ve |DO| = |OB| dir.

Paralelkenarda Uzunluk

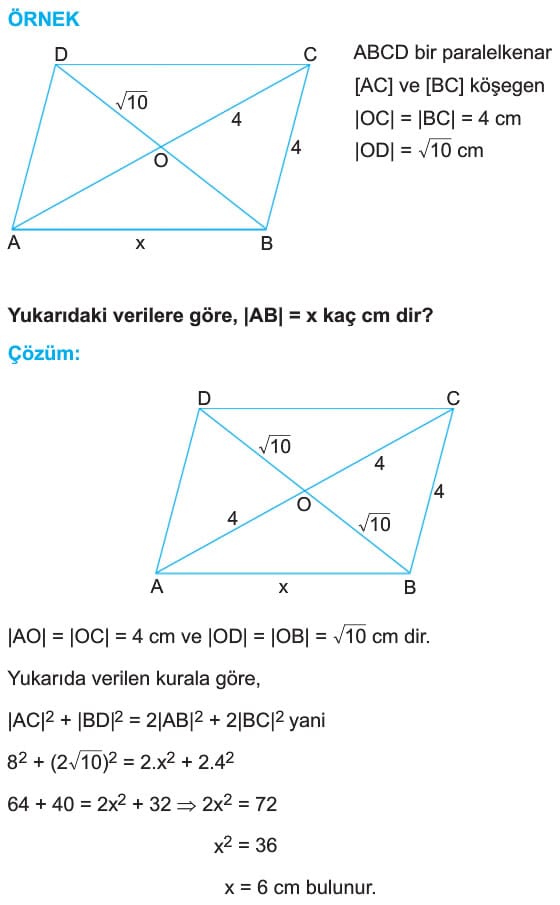
Paralelkenarda köşegenler birbirini ortalar ve köşegen uzunluklarının kareleri toplamı kenar uzunluklarının kareleri toplamına eşittir. Yani, ABCD paralelkenarında
|AC|² + |BD|² = 2a² + 2b² dir.

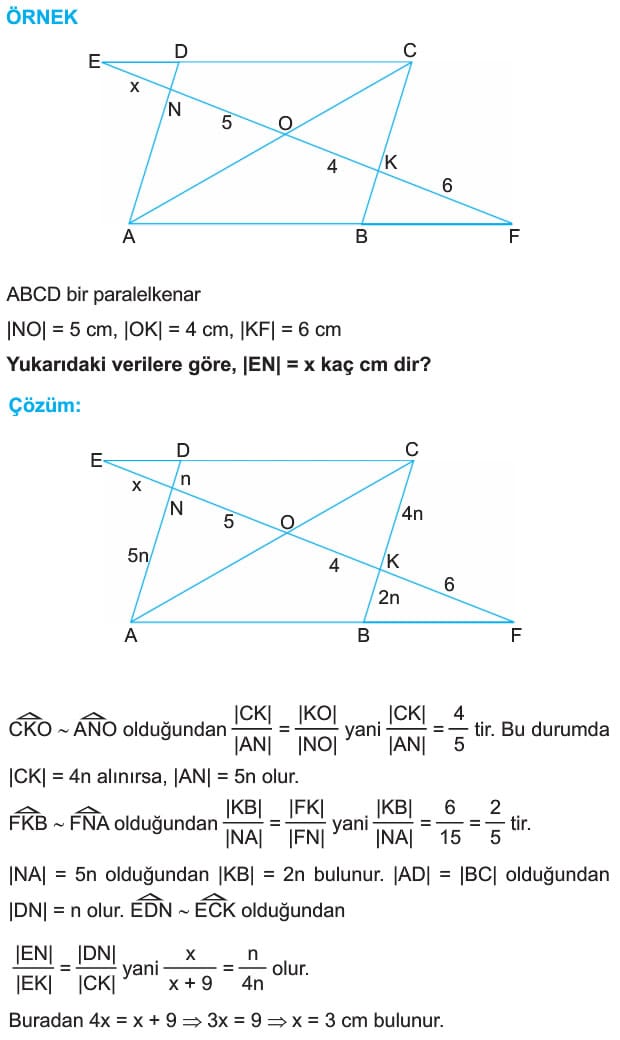
Çözümlü Sorular

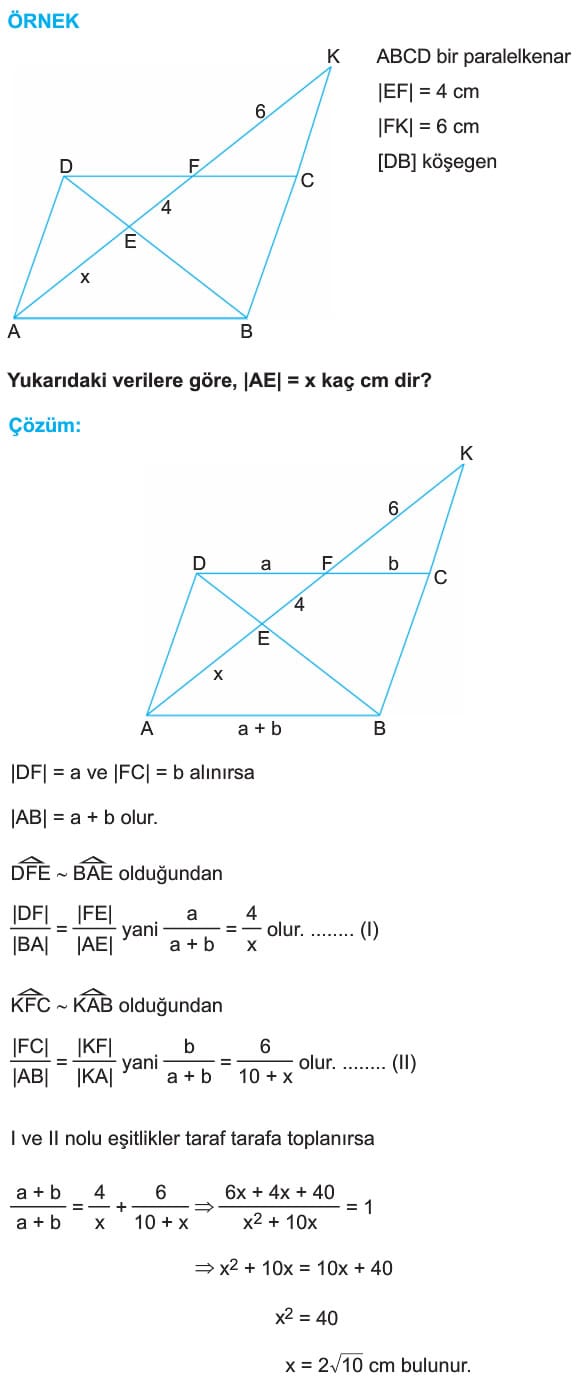
Çözümlü Sorular

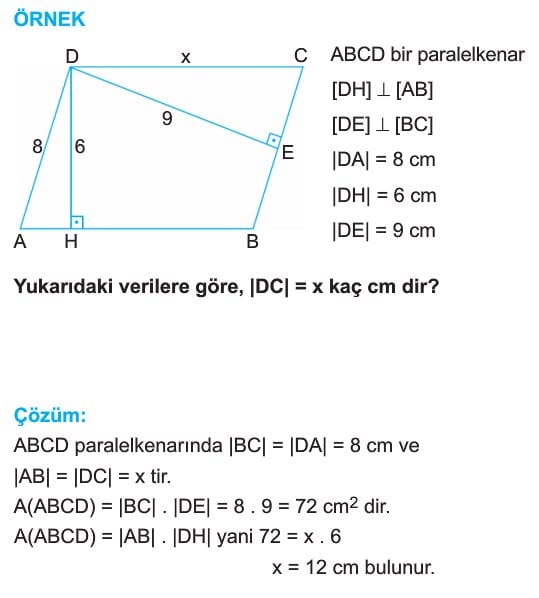
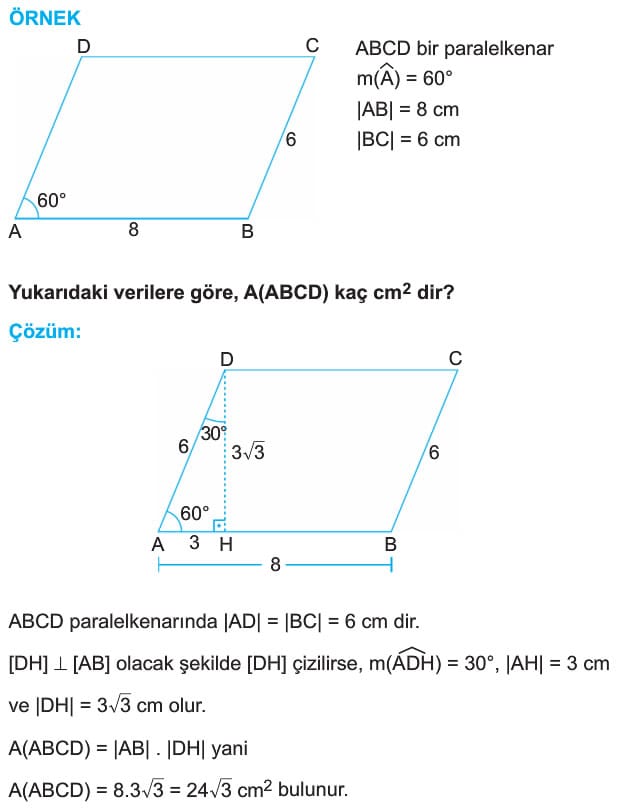
PARALELKENARDA ALAN

Paralelkenarın alanı, bir kenar uzunluğu ile o kenara ait yüksekliğin çarpımına eşittir.

A(ABCD) = a . h_a veya
A(ABCD) = b . h_b dir.

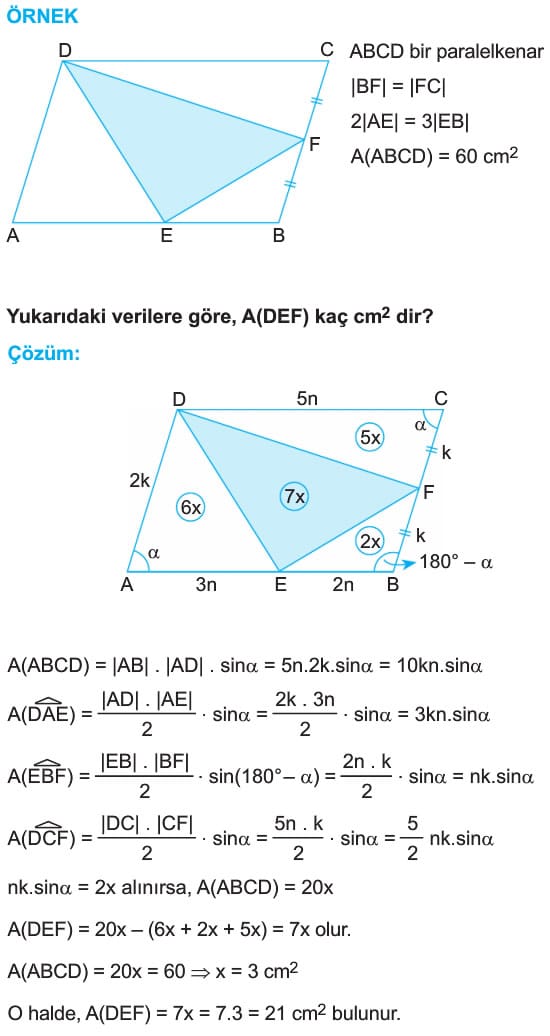
Çözümlü Sorular

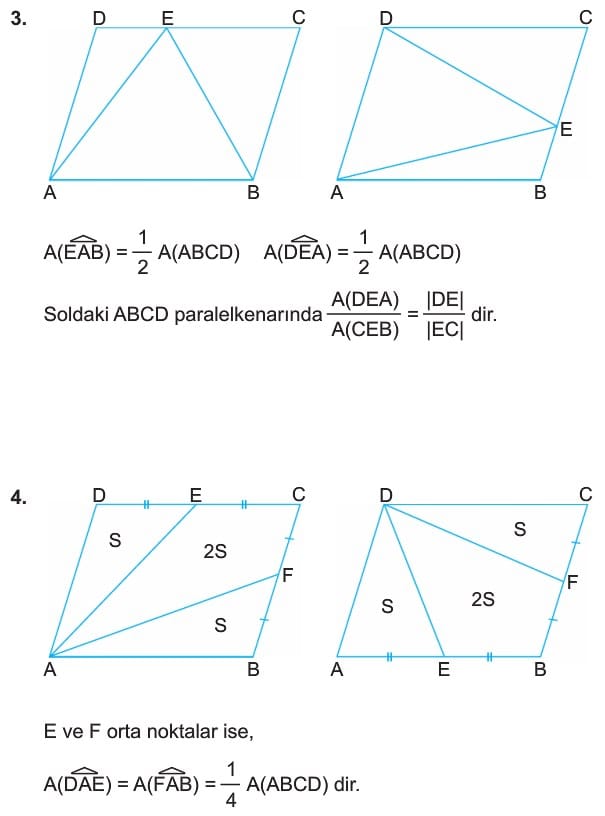
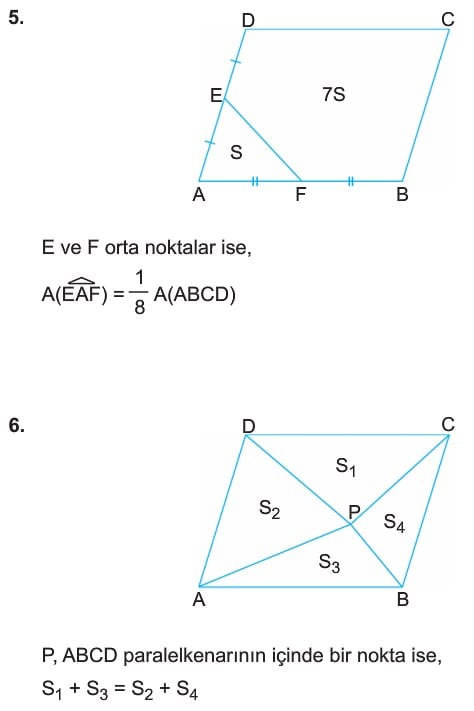
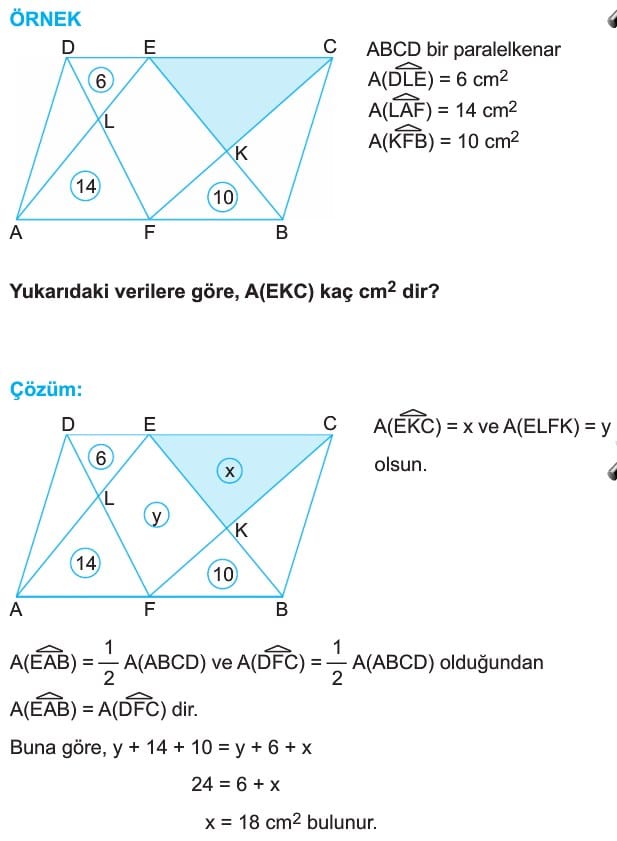
PARALELKENARDA ALAN ORANLARI

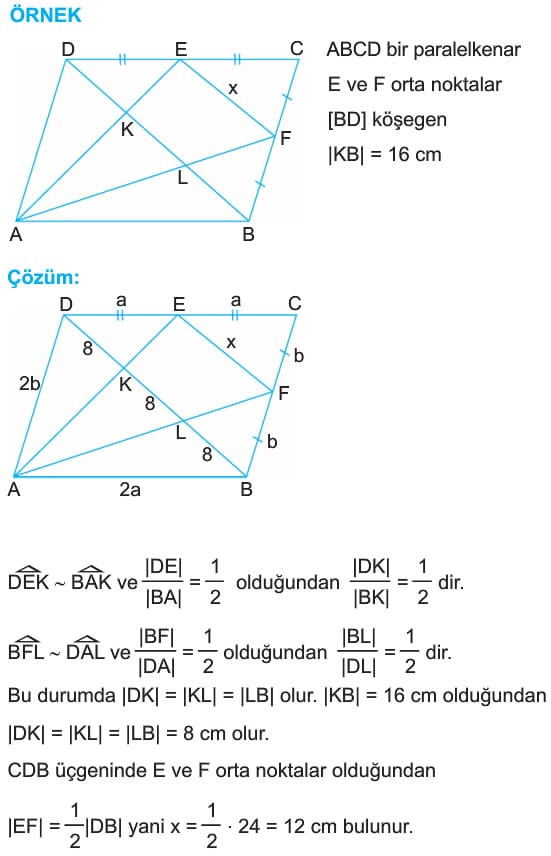
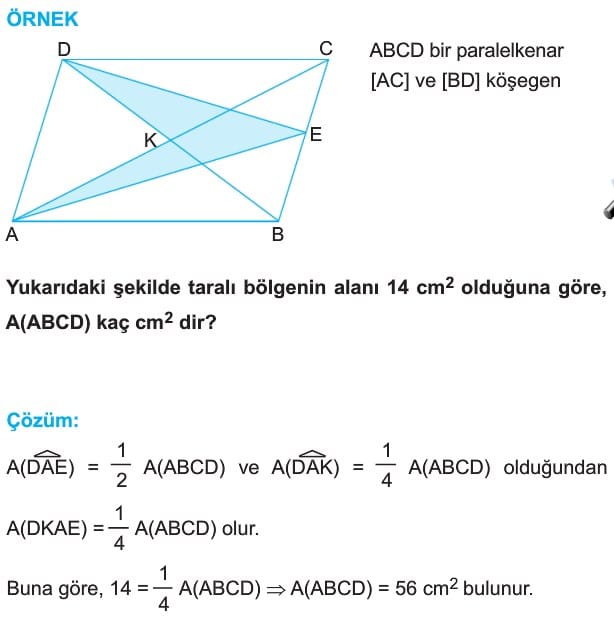
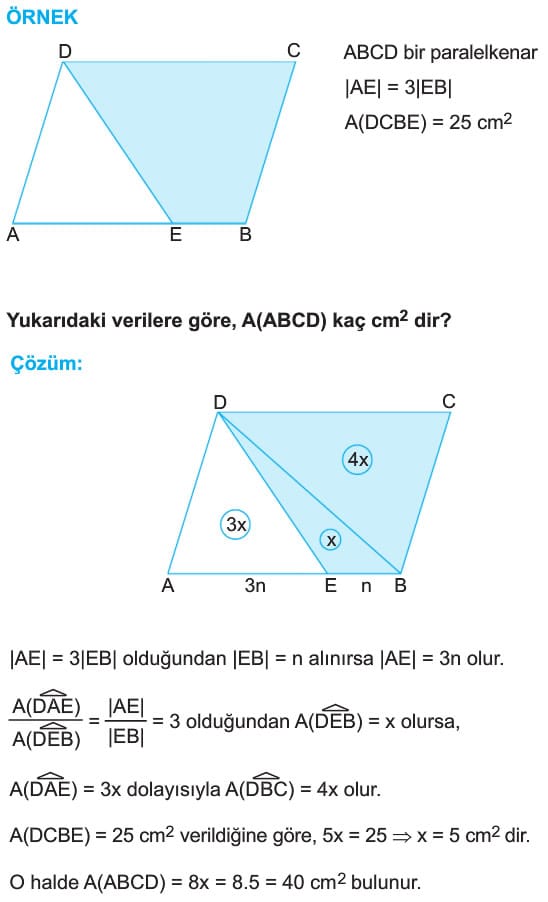
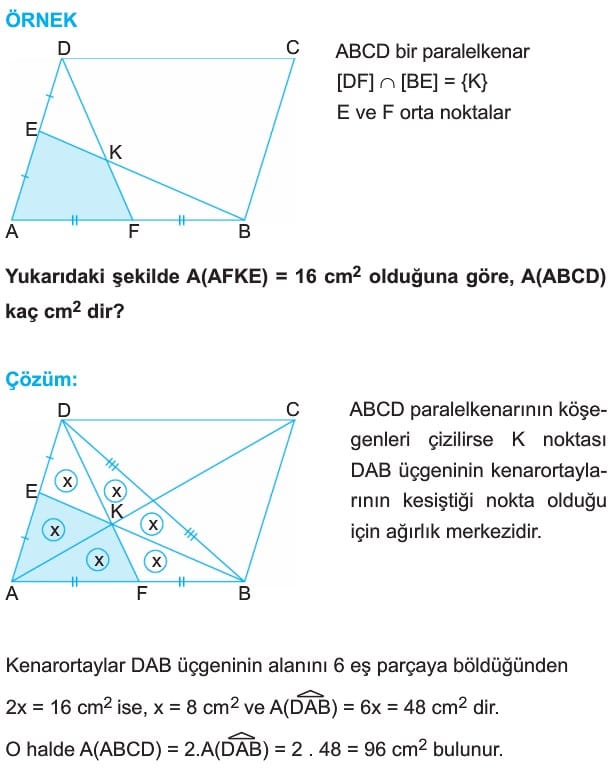
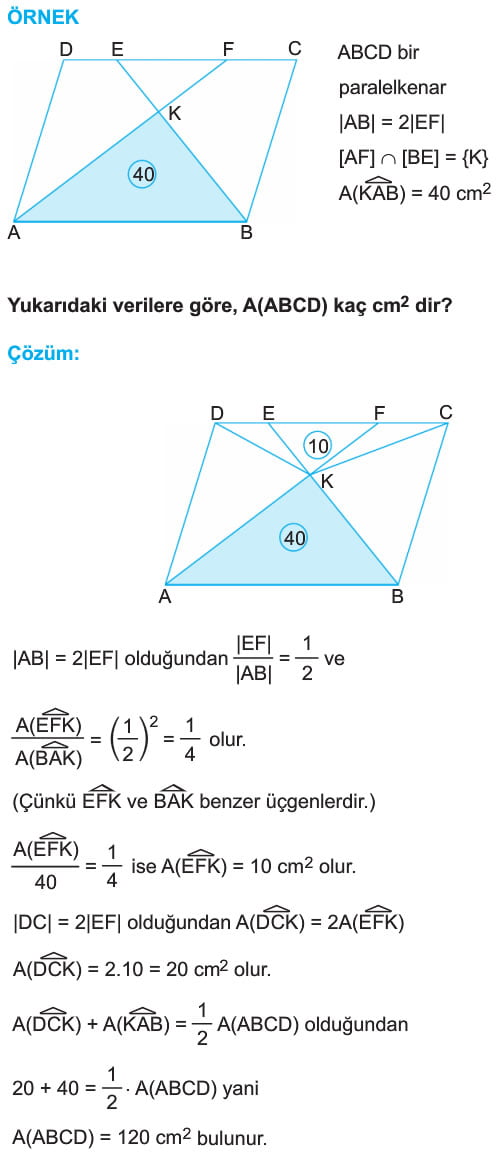
Çözümlü Sorular 

Çözümlü Örnek Test Soruları

Soru 1
Bir paralelkenarın karşılıklı kenarlarının özellikleri aşağıdakilerden hangisidir?
A) Paralel ve eşit uzunluktadır
B) Paralel ve farklı uzunluktadır
C) Birbirine dik ve eşit uzunluktadır
D) Paralel ve bir açı yapar
E) Birbirine dik ve farklı uzunluktadır

Çözüm
Paralelkenarın karşılıklı kenarları hem paralel hem de eşit uzunluktadır.
Cevap: A

Soru 2
Bir paralelkenarın karşılıklı açılarının ölçüleriyle ilgili doğru olan ifade hangisidir?
A) Birbirine eşit değildir
B) Birbirine dik açılardır
C) Birbirine eşittir
D) Toplamları 360 derecedir
E) Bir açısı 90 derecedir

Çözüm
Paralelkenarda karşılıklı açılar eşittir.
Cevap: C

Soru 3
Bir paralelkenarın çevresi hesaplanırken kullanılan formül aşağıdakilerden hangisidir?
A) 2 × (a + b)
B) a × b
C) a + b
D) 2 × a
E) 2 × b

Çözüm
Paralelkenarın çevresi, karşılıklı iki kenar uzunluğunun toplamının iki katı olarak bulunur: 2 × (a + b).
Cevap: A

Soru 4
Taban uzunluğu 8 cm, yüksekliği 5 cm olan bir paralelkenarın alanı kaç santimetrekaredir?
A) 20 cm²
B) 25 cm²
C) 30 cm²
D) 40 cm²
E) 50 cm²

Çözüm
Paralelkenarın alanı, taban uzunluğu ile yüksekliğin çarpımı ile bulunur. 8 × 5 = 40 cm².
Cevap: D

Soru 5
Bir paralelkenarın alanı 60 cm², taban uzunluğu 10 cm ise yüksekliği kaç cm olur?
A) 4 cm
B) 5 cm
C) 6 cm
D) 7 cm
E) 8 cm

Çözüm
Paralelkenarın alanı = taban × yükseklik. Buradan yükseklik = 60 / 10 = 6 cm.
Cevap: C

Soru 6
Kenar uzunlukları 7 cm ve 12 cm olan bir paralelkenarın çevresi kaç cm’dir?
A) 19 cm
B) 24 cm
C) 38 cm
D) 45 cm
E) 56 cm

Çözüm
Paralelkenarın çevresi, karşılıklı kenarların toplamının iki katıdır: 2 × (7 + 12) = 38 cm.
Cevap: C

Soru 7
Bir paralelkenarın bir açısının ölçüsü 60 derece ise karşısındaki açının ölçüsü kaç derecedir?
A) 30°
B) 60°
C) 90°
D) 120°
E) 150°

Çözüm
Paralelkenarda karşılıklı açılar eşittir, bu yüzden karşıdaki açı da 60°’dir.
Cevap: B

Soru 8
Alanı 84 cm² olan bir paralelkenarın taban uzunluğu 14 cm olduğuna göre yüksekliği kaç cm’dir?
A) 5 cm
B) 6 cm
C) 7 cm
D) 8 cm
E) 9 cm

Çözüm
Paralelkenarın alanı = taban × yükseklik. Buradan yükseklik = 84 / 14 = 6 cm.
Cevap: B

Paralelkenar  konusu 11. sınıf geometri dersi müfredatında yer almakta olup ygs, lys ve kpss matematik sınavlarında soru gelebilmektedir.

• Paralelkenar konu anlatımı videosunda anlatılan konu başlıkları,
• Paralelkenar tanımı nedir
• Paralelkenarın kenarları, açıları ve köşegenleri ile ilgili özellikler
• Paralelkenarın alan bağıntısı

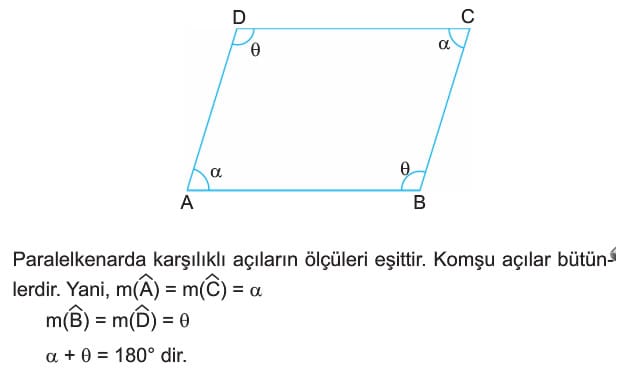
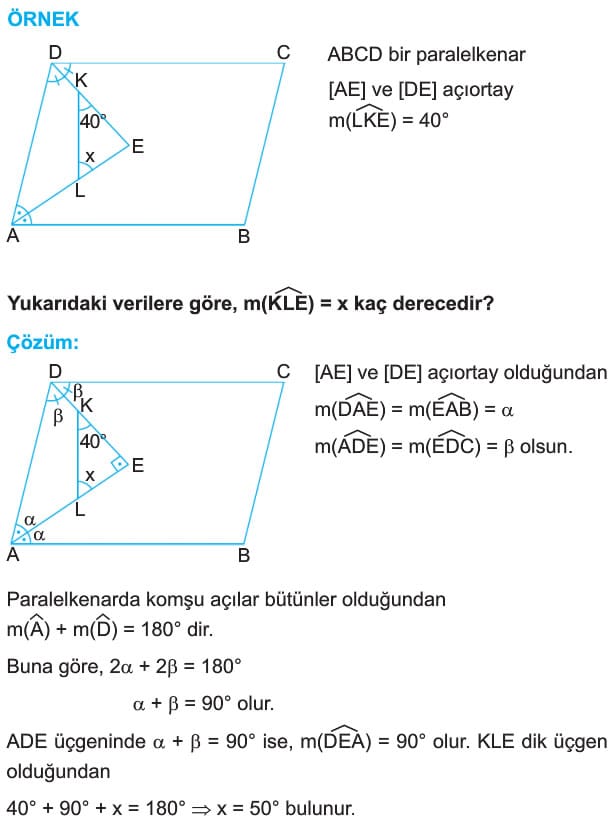
• Paralelkenarda karşılıklı açıların ölçüleri eşittir. Komşu açılar bütünlerdir. Yani, m(A) = m(C) = alfa
  m(B) = m(D) = beta
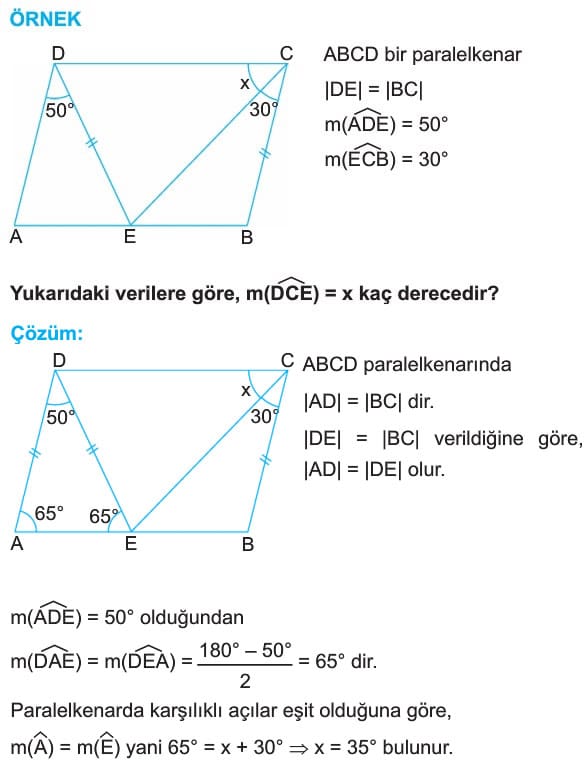
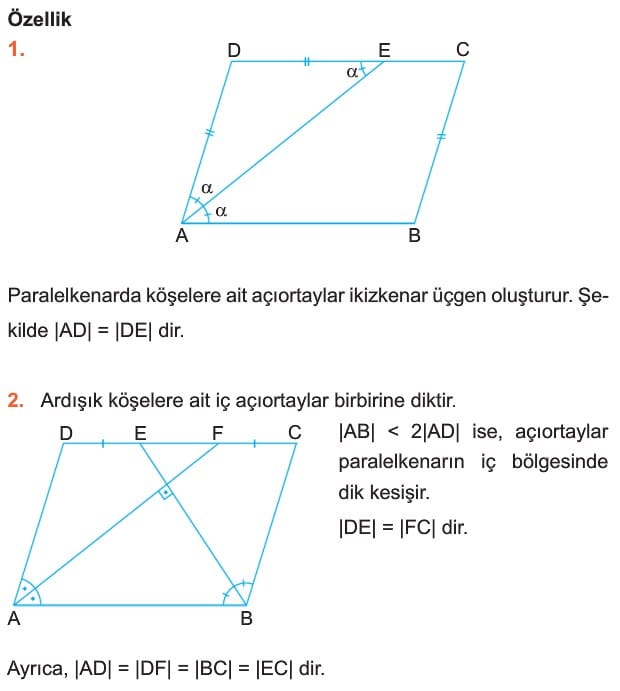
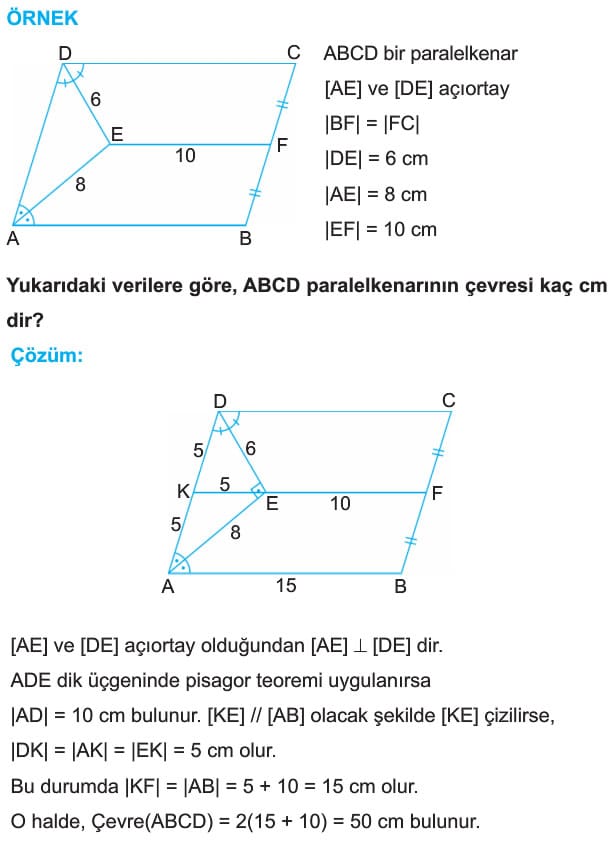
  alfa + beta =180° dir.
• Paralelkenarda köşelere ait açıortaylar ikizkenar üçgen oluşturur. Şekilde |AD| = |DE| dir.
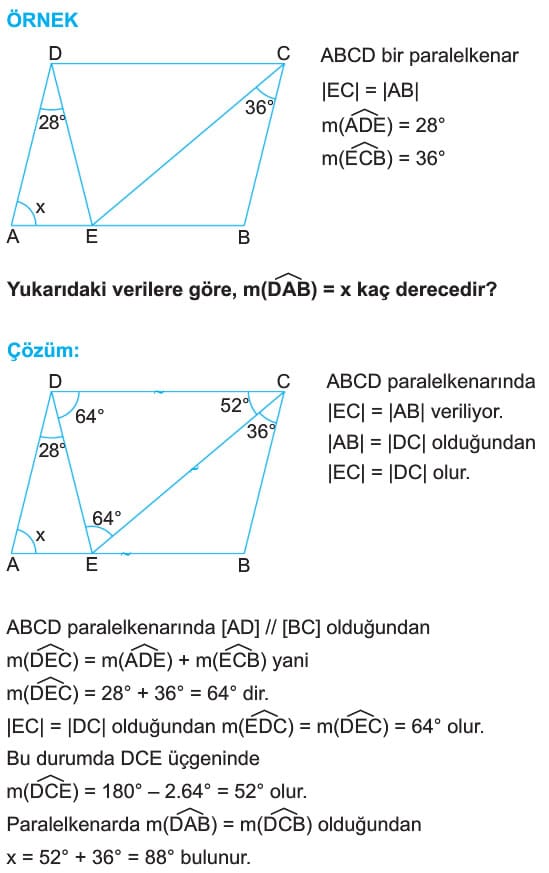
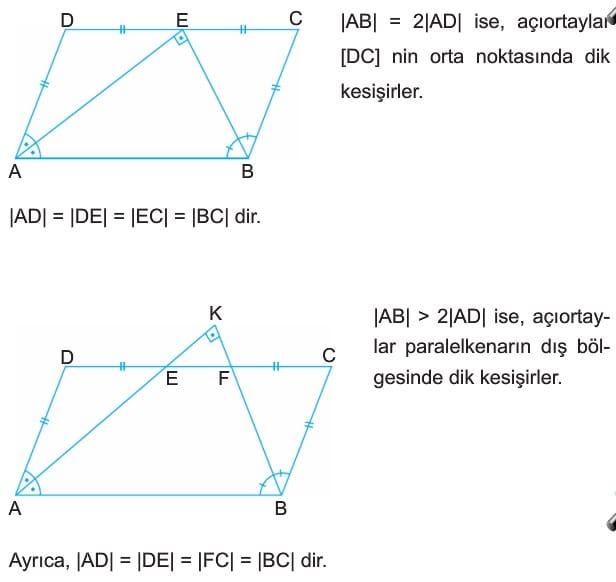
• Ardışık köşelere ait iç açıortaylar birbirine diktir. |AB| < 2|AD| ise, açıortaylar paralelkenarın iç bölgesinde dik kesişir. |DE| = |FC| dir.
  Ayrıca, |AD| = |DF| = |BC| = |EC| dir.
  |AB| = 2|AD| ise, açıortaylar [DC] nin orta noktasında dik kesişirler.
  |AD| = |DE| = |EC| = |BC| dir.
  |AB| > 2|AD| ise, açıortaylar paralelkenarın dış bölgesinde dik kesişirler.
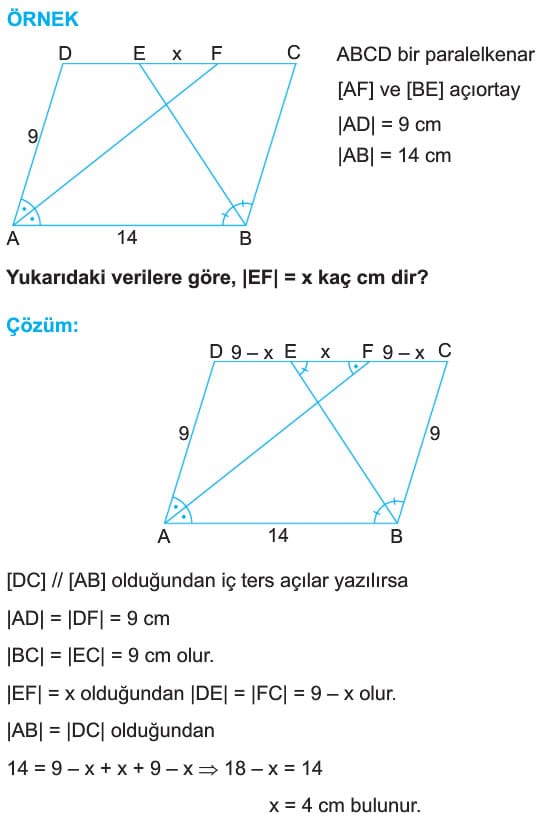
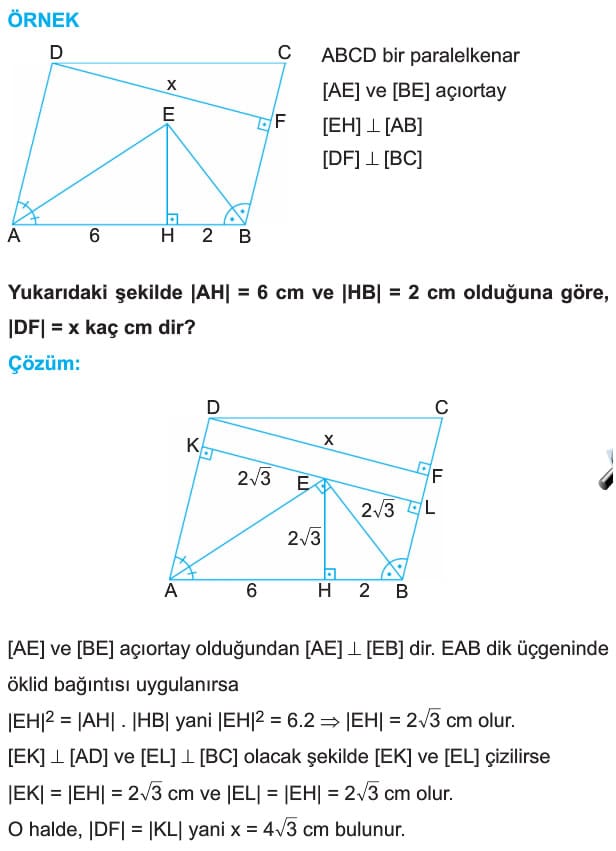
  Ayrıca, |AD| = |DE| = |FC| = |BC| dir.
• ÖRNEK: ABCD bir paralelkenar
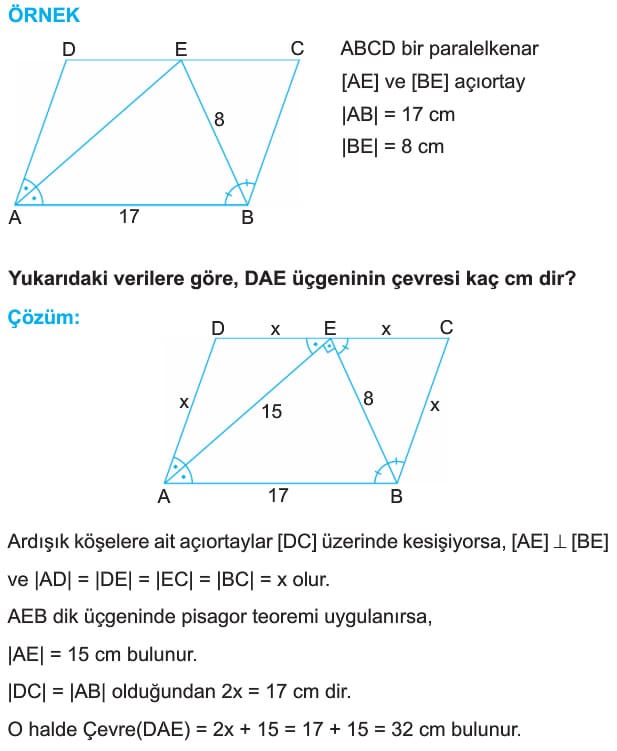
  [AE] ve [BE] açıortay
  |AB| = 17 cm
  |BE| = 8 cm
  Yukarıdaki verilere göre, DAE üçgeninin çevresi kaç cm dir?
  Çözüm: Ardışık köşelere ait açıortaylar [DC] üzerinde kesişiyorsa, [AE] dik [BE] ve |AD| = |DE| = |EC| = |BC| = x olur.
  AEB dik üçgeninde pisagor teoremi uygulanırsa,
  |AE| = 15 cm bulunur.
  |DC| = |AB| olduğundan 2x = 17 cm dir.
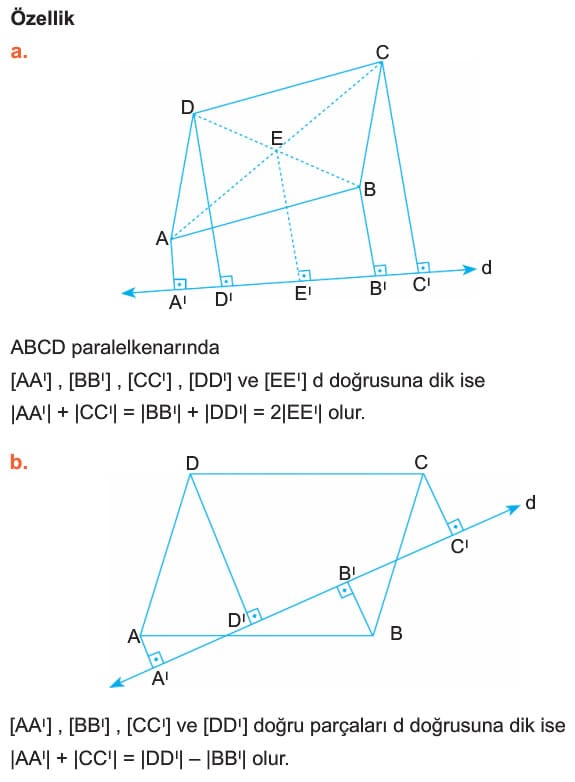
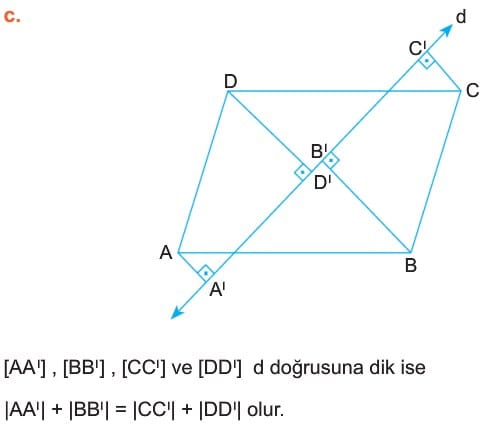
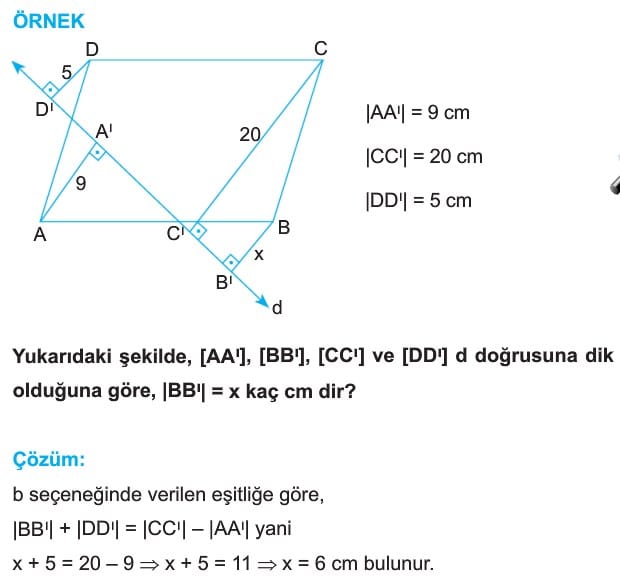
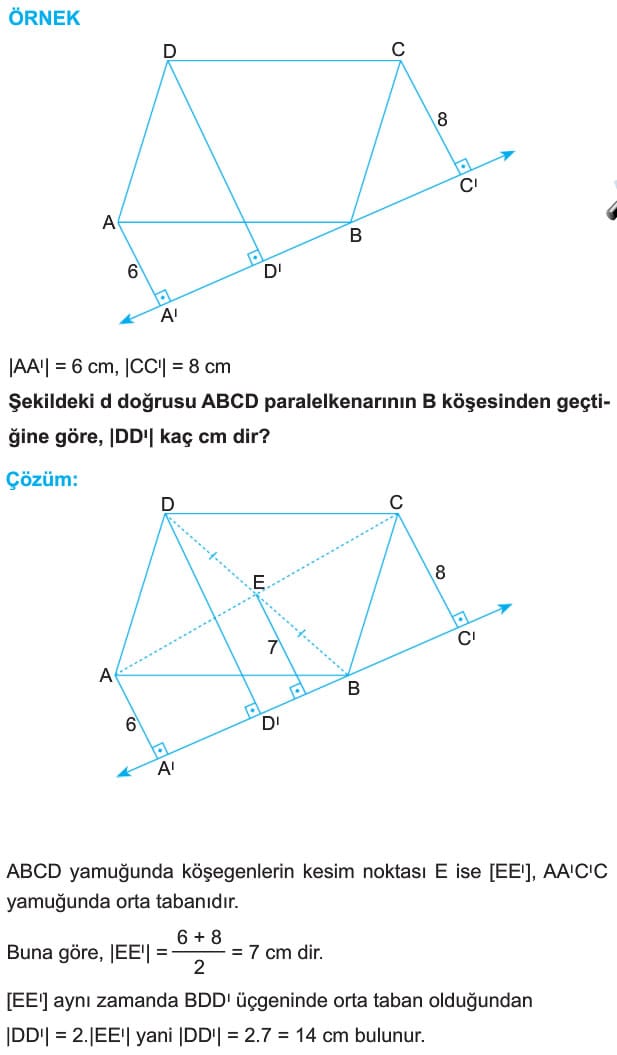
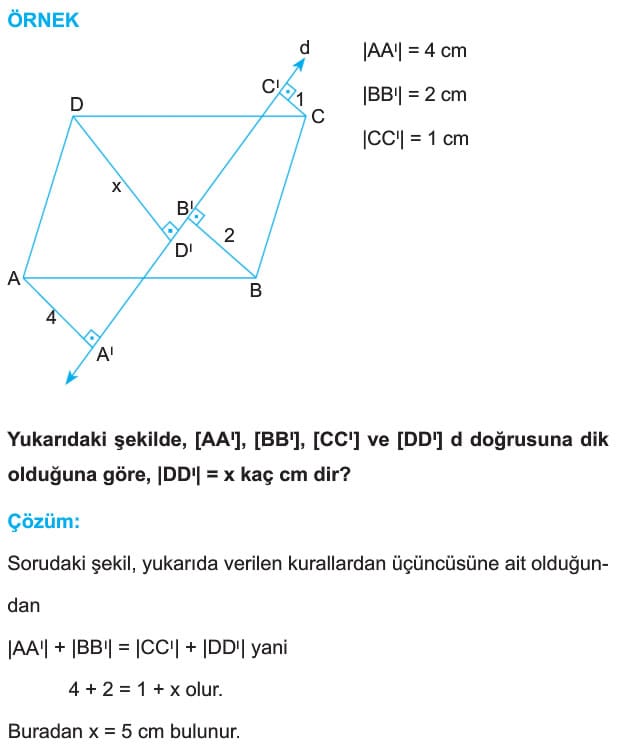
  O halde Çevre(DAE) = 2x +15 = 17 +15 = 32 cm bulunur.
• ABCD paralelkenarının köşelerinden paralelkenarın dışındaki bir doüruya dikmeler çizlirse,karşılıklı köşelerden indirilen dikmelerin uzunlukları toplamı birbirlerine eşittir. Eğer paralelkenarı kesen bir doğruya bu dikmeler çizilirse A ve C köşelerinden çizilen dikmelerin uzunlukları toplamı diğer köşelerden çizilen dikmelerin uzunluklarının farkına eşittir.
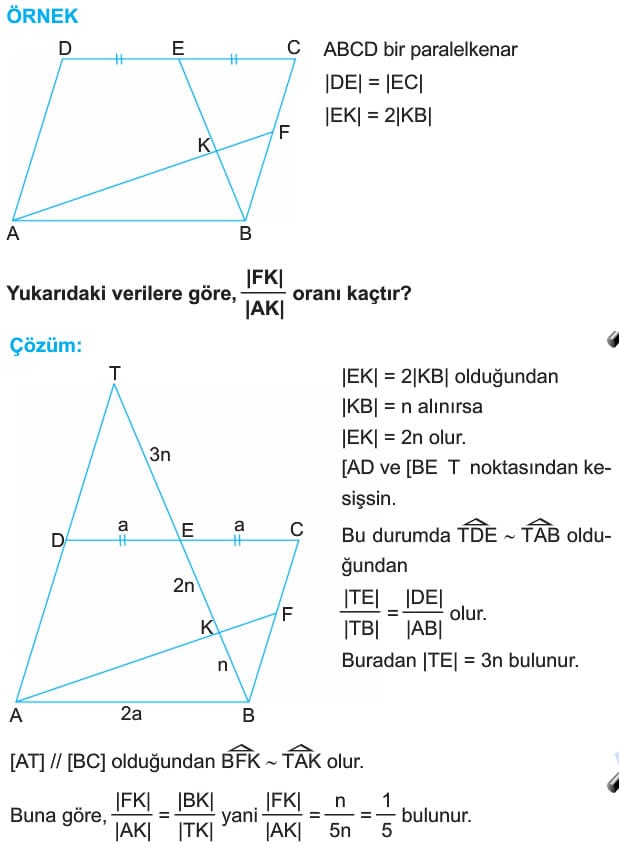
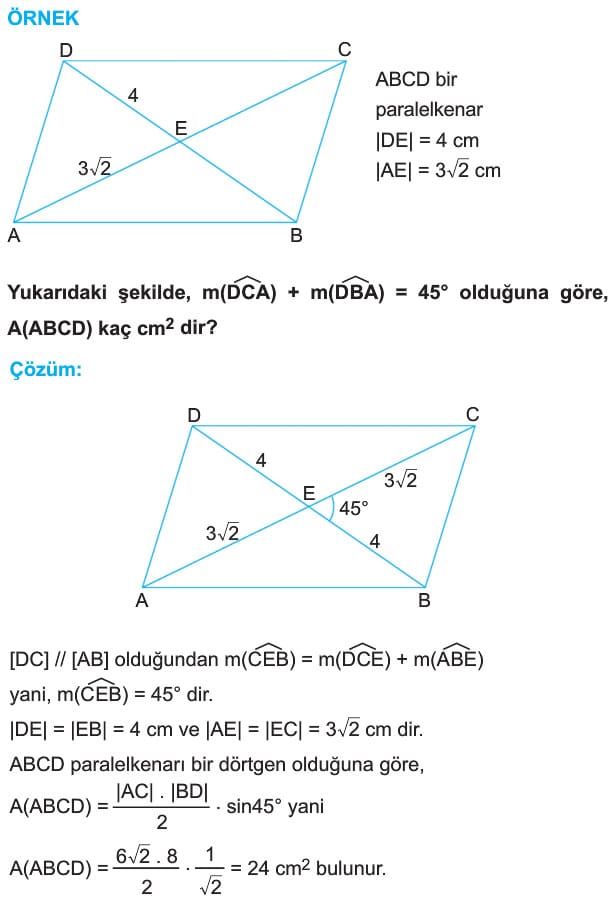
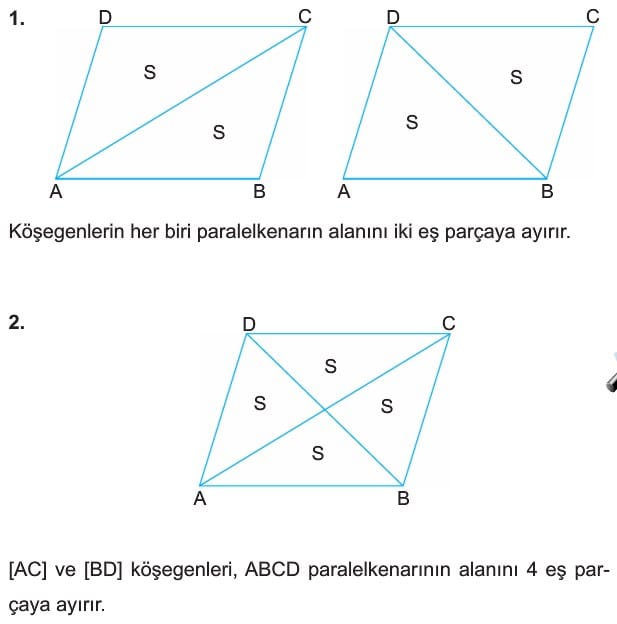
• Köşegenlerin her biri paralelkenarın alanını iki eş parçaya ayırır. [AC] ve [BD] köşegenleri, ABCD paralelkenarının alanını 4 eş parçaya ayırır.

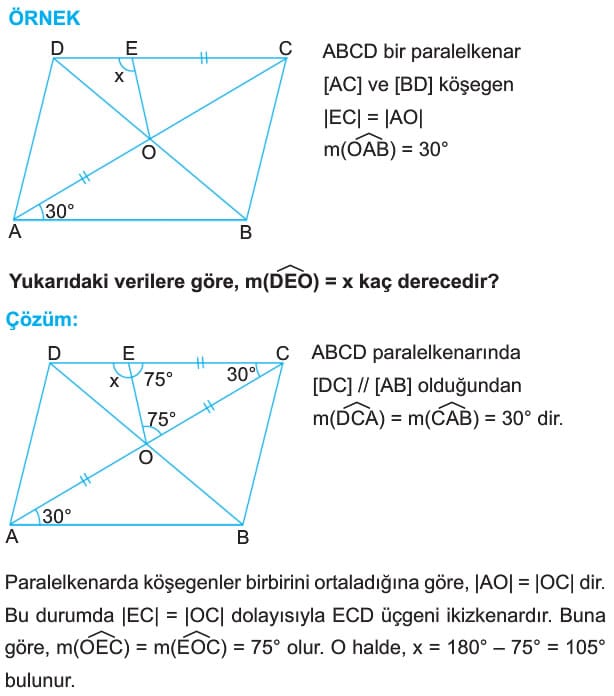
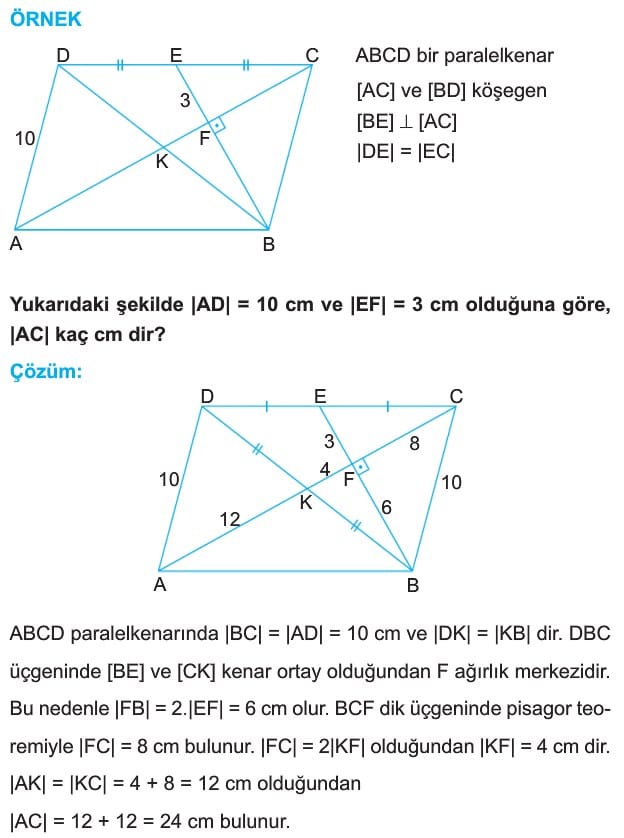
ÖRNEK: ABCD bir paralelkenar,
[AC] ve [BD] köşegen
[BE] dik [AC]
|DE| = |EC|
Yukarıdaki şekilde |AD| = 10 cm ve |EF| = 3 cm olduğuna göre, |AC| kaç cm dir?
Çözğm: ABCD paralelkenarında |BC| = |AD| = 10 cm ve |DK| = |KB| dir. DBC üçgeninde [BE] ve [CK] kenar ortay olduğundan F ağırlık merkezidir. Bu nedenle |FB| = 2.|EF| = 6 cm olur. BCF dik üçgeninde pisagorteoremiyle |FC| = 8 cm bulunur. |FC| = 2|KF| olduğundan |KF| = 4 cm dir. |AK| = |KC| = 4 + 8 = 12 cm olduğundan |AC| = 12 +12 = 24 cm bulunur.