Özdeşlikler 8. Sınıf

Kategoriler: 8. Sınıf Matematik, Matematik

Bilinmeyenin her değeri için doğru olan yani çözümü R (Gerçek Sayılar) olan eşitliklere özdeşlik denir. Özdeşlikler, içerdikleri değişkenlere verilecek bütün gerçek sayılar için, denklemler ise bazı gerçek sayılar için doğrudur.

Dikkat: Verilen eşitliklerde değişkenlere değer vermek yerine, eşitliğin her iki yanındaki cebirsel ifadeleri en sade hallerinde yazıp eşit çıkıp çıkmadıklarına bakmak daha uygundur. Eşitliğin her iki yanındaki cebirsel ifadelerin en sade hâlleri aynı çıkarsa eşitlik özdeşlik olur.

1. İKİ TERİMİN TOPLAMININ KARESİ ÖZDEŞLİĞİ

Önemli Bilgi:

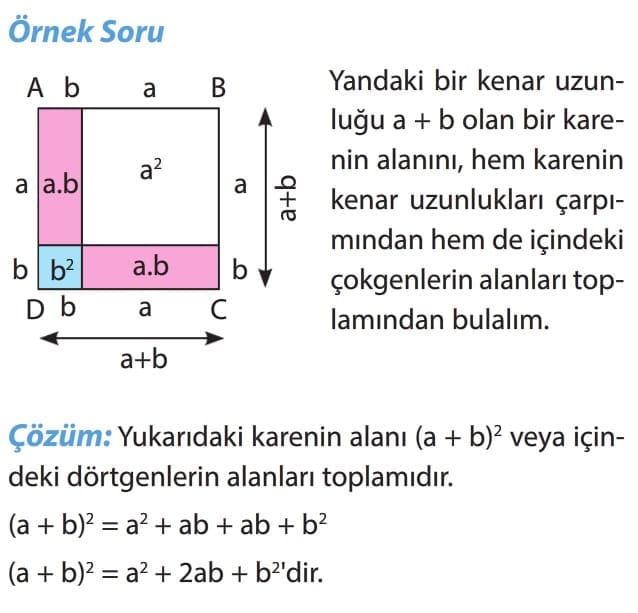
(a + b)2 = a2 + 2ab + b2

İki terimin toplamının karesi alınırken birinci terimin karesi, birinci ile ikinci terimin çarpımlarının iki katı ve ikinci terimin karesi toplanır.

Dikkat: Özdeşliklerin modellenmesinde verilen dörtgenin kenar uzunluklarının çarpımı özdeşliği verir.

2. İKİ TERİMİN FARKININ KARESİ ÖZDEŞLİĞİ

Önemli Bilgi:

(a – b)2 = a2 – 2ab + b2

İki terimin farkının karesi alınırken birinci terimin karesinden birinci terim ile ikinci terimin çarpımlarının 2 katı çıkarılır ve ikinci terimin karesi toplanır.

3. İKİ KARE FARKI ÖZDEŞLİĞİ

Önemli Bilgi:

a2 – b2 = (a – b) . (a + b)

İki terimin farkı ile toplamının çarpımı bu terimlerin kareleri farkına eşittir.

] }

Örnek Soru: 3 . (x + 6) = 2. (x + 1) ifadesinin özdeşlik mi denklem mi olduğunu inceleyelim.
Çözüm: 3 . (x + 6) = 2 . (x + 1)
3 . x + 3 . 6 = 2 . x + 2 . 1
3x + 18 = 2x + 2
3x - 2x = 2 - 18
x = -16
3 . (x + 6) = 2 . (x + 1) eşitliği sadece -16 değeri için doğru olur. Bundan dolayı 3 . (x + 6) = 2 . (x + 1) ifadesi bir denklemdir.

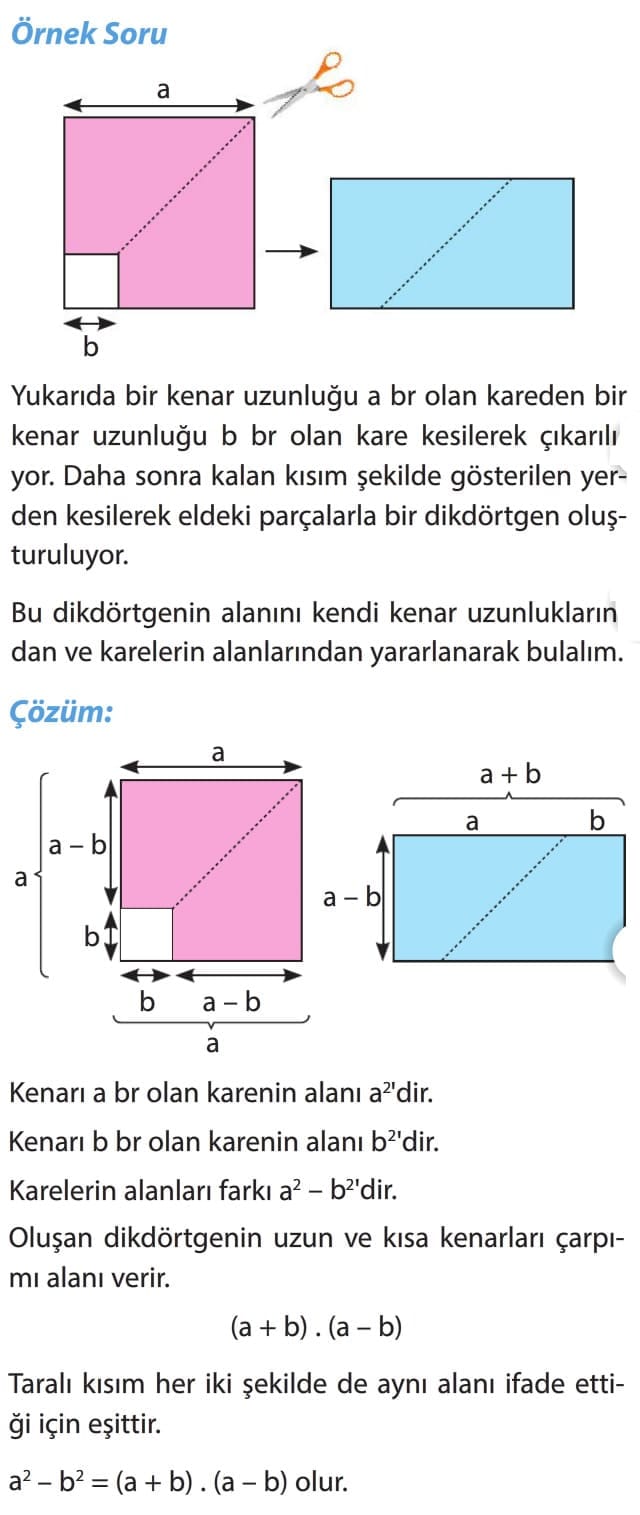
Örnek Soru: Bir kenar uzunluğu a br olan kareden, bir kenar uzunluğu b br olan bir kare kesilip çıkarılıyor. Buna göre, kalan bölgenin alanını gösteren cebirsel ifadenin özdeşini bulalım.
Çözüm: Büyük karenin alanından küçük karenin alanını çıkarırsak geriye kalan bölgenin alanını buluruz.
Büyük karenin alanı = a . a = a2
Küçük karenin alanı = b . b = a2
Kalan bölge alanı a2 - b2'dir.
Buna göre ifadenin özdeşi a2 - b2 = (a + b) . (a - b)'dir.

Örnek Soru: Bir takımda yedek olmayan a tane oyuncunun her biri a dakika, yedek olan b tane oyuncunun her biri b dakika oynamıştır. Buna göre, yedek olmayan ve yedek olan oyuncuların maçtaki oynadıkları toplam süre farkını kullanarak aşağıdaki özdeşliklerden hangisi yazılabilir?
A) a2 + b2  = (a + b)2 - 2ab
B) (a-b2=a2-2ab+b2
C) (a + b)2 = a2+2ab+b2
D) a2 - b2 =( a - b) . (a + b)
Çözüm: Yedek olmayan a tane oyuncunun maçta aldığı süre: a . a = a2 dir.
Yedek olan b tane oyuncunun maçta aldığı süre: b . b = b2'dir.
Yedek olmayan ve yedek olan oyuncuların maçta  aldıkları süre farkı: a2 - b2'dir.
Buna göre, az - bz = (a - b) . (a + b) özdeşliği elde edilir. Yanıt D

Elbette! Özdeşlikler, matematikte temel kavramlardan biridir. İşte 8. sınıf seviyesinde özdeşliklerle ilgili bazı temel konular:

  • Eşitlik ve Eşdeğerlik:
    • Eşitlik ifadeleri: İki tarafı eşit olan ifadelerdir. Örneğin: 3x + 2 = 11.
    • Eşdeğerlik ifadeleri: İki tarafı eşit olan ifadeler, bazı değişkenlerin yerine konduğunda aynı değeri veren ifadelerdir. Örneğin: 2(x + 3) ve 2x + 6 eşdeğerdir.
  • Özdeşlikler:
    • Özdeşlik ifadeleri: Herhangi bir değer yerine konulduğunda her zaman doğru olan ifadelerdir. Örneğin: (a + b)^2 = a^2 + 2ab + b^2.
  • Denklem ve İkilikler:
    • Denklem: Bir veya daha fazla bilinmeyenin yerine konduğunda doğru sonuç veren ifadedir. Örneğin: 4x + 7 = 15.
    • İkilik: İki ifade arasında denklik ilişkisi kurulduğunda oluşan ifadelerdir. Örneğin: (x + 3)(x - 3) = x^2 - 9.
  • İkilik Özdeşlikleri:
    • İkilik özdeşlikleri, iki terimin çarpımını veya toplamını ifade eden özdeşliklerdir. Örneğin: (a + b)^2 = a^2 + 2ab + b^2.
  • Değişmezlik Özdeşlikleri:
    • Değişmezlik özdeşlikleri, bir ifadenin belirli bir değişiklik sonucu aynı kaldığını ifade eden özdeşliklerdir. Örneğin: x + y = y + x.
  • Dağılma Özdeşlikleri:
    • Dağılma özdeşlikleri, çarpma veya bölme işlemi sırasında dağılma özelliğini ifade eden özdeşliklerdir. Örneğin: a(b + c) = ab + ac.
  • İkilik Teoremleri:
    • İkilik teoremleri, ikilik ifadelerin kuvvetlerini ifade eden özdeşliklerdir. Örneğin: (a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3.
  • Üstel Özdeşlikler:
    • Üstel özdeşlikler, üs kavramını içeren özdeşliklerdir. Örneğin: a^(m + n) = a^m * a^n.

    • Bu konular, 8. sınıf seviyesinde özdeşliklerle ilgili temel kavramları içerir. Daha karmaşık özdeşlikler ve konuları da öğrenebilirsiniz, ancak bu temel kavramlar önemli bir başlangıç noktası olacaktır.

    Liselere Giriş Sınavı (LGS)
    5 Haziran 2022 Pazar
    Temel Yeterlilik Sınavı (TYT)
    18 Haziran 2022 Cumartesi
    Alan Yeterlilik Sınavı (AYT)
    19 Haziran 2022 Pazar