Oran Orantı Problemleri ve Çözümleri

Çözümlü Örnek Test Soruları

Soru 1:
Bir sınıfta kızların sayısının erkeklerin sayısına oranı 3/5’tir. Sınıfta 15 kız varsa, kaç erkek vardır?

A) 20
B) 25
C) 30
D) 35
E) 40

Çözüm:
Kızların sayısı 3 birim, erkeklerin sayısı 5 birim olarak düşünülür. Eğer 3 birim 15’e denk geliyorsa, 1 birim 15 / 3 = 5 olur. Erkeklerin sayısı 5 birim olduğuna göre, 5 * 5 = 25 bulunur.
Cevap: B

Soru 2:
Bir proje için iki öğrenciye iş dağıtımı yapılmıştır. Ali’nin tamamladığı işin miktarının, Veli’nin tamamladığı işin miktarına oranı 2/3’tür. Eğer Ali 20 iş birimi tamamladıysa, Veli’nin tamamladığı iş miktarı kaç birimdir?

A) 25
B) 30
C) 35
D) 40
E) 45

Çözüm:
Ali’nin yaptığı iş miktarı 2 birim, Veli’nin yaptığı iş miktarı 3 birimdir. Ali’nin iş miktarı 20 birime denk geldiğine göre, 1 birim 20 / 2 = 10’dur. Veli 3 birim iş yaptığı için, 3 * 10 = 30 iş birimi tamamlamıştır.
Cevap: B

Soru 3:
Bir işin 3/4’ü 18 günde tamamlanıyorsa, işin tamamı kaç günde biter?

A) 20
B) 22
C) 24
D) 28
E) 30

Çözüm:
3/4 iş 18 günde yapılıyorsa, işin tamamı 18 * (4/3) = 24 günde tamamlanır.
Cevap: C

Soru 4:
Bir üçgenin kenar uzunlukları 5 : 12 : 13 oranındadır. Üçgenin en uzun kenarı 26 cm ise, en kısa kenarı kaç cm’dir?

A) 5
B) 10
C) 15
D) 20
E) 25

Çözüm:
En uzun kenar 13 birime denk geliyorsa ve 13 birim = 26 cm ise, 1 birim 26 / 13 = 2 cm’dir. En kısa kenar 5 birim olduğundan, 5 * 2 = 10 cm bulunur.
Cevap: B

Soru 5:
Bir sınıfta öğrencilerin matematik ve fizik dersindeki başarı oranı 4 : 3’tür. Eğer matematik dersinde başarılı olan öğrenci sayısı 20 ise, fizik dersinde başarılı olan öğrenci sayısı kaçtır?

A) 12
B) 13
C) 15
D) 18
E) 24

Çözüm:
Matematik dersinde başarılı öğrenci sayısı 4 birim, fizik dersinde başarılı öğrenci sayısı 3 birimdir. Matematikteki 4 birim 20 öğrenciye karşılık geldiğinden, 1 birim 20 / 4 = 5’tir. Fizikte başarılı olan öğrenci sayısı 3 * 5 = 15 olur.
Cevap: C

Soru 6:
Bir miktar para Ali, Veli ve Can arasında 2 : 3 : 5 oranında paylaştırılıyor. Veli 30 TL aldığına göre, toplam para kaç TL’dir?

A) 60
B) 80
C) 90
D) 100
E) 120

Çözüm:
Veli’nin aldığı miktar 3 birime karşılık geldiğine göre, 1 birim 30 / 3 = 10 TL’dir. Toplam para 2 + 3 + 5 = 10 birim olduğuna göre, toplam para 10 * 10 = 100 TL olur.
Cevap: D

Soru 7:
Bir ormanda yaşları oranı 3 : 4 olan iki ağaç bulunmaktadır. Küçük ağaç 15 yaşında olduğuna göre, büyük ağacın yaşı kaçtır?

A) 18
B) 20
C) 25
D) 30
E) 35

Çözüm:
Küçük ağacın yaşı 3 birime karşılık geldiğine göre, 1 birim 15 / 3 = 5 olur. Büyük ağaç 4 birim yaşında olduğundan, büyük ağacın yaşı 4 * 5 = 20’dir.
Cevap: B

Soru 8:
Bir şirkette çalışan mühendislerin sayısının teknikerlerin sayısına oranı 7 : 3’tür. Şirkette 21 mühendis varsa, kaç tekniker vardır?

A) 7
B) 8
C) 9
D) 10
E) 12

Çözüm:
Mühendislerin sayısı 7 birime karşılık geldiğine göre, 1 birim 21 / 7 = 3’tür. Teknikerlerin sayısı 3 birim olduğuna göre, 3 * 3 = 9 olur.
Cevap: C

Soru 9:
Bir iş yerinde yapılan işin oranı ilk 2 gün 1 : 3, sonraki 3 gün 3 : 5 oranında tamamlanmıştır. Eğer ikinci kısımda yapılan iş miktarı 15 birimse, toplam iş miktarı kaç birimdir?

A) 22
B) 25
C) 28
D) 30
E) 40

Çözüm:
İlk orantıya göre yapılan iş miktarı (ilk kısım) 4 olup, ikinci kısım 15 birim olmuştur.

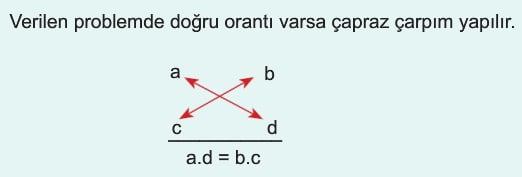
Doğru orantı problemlerinde ifadeler çapraz olarak çarpılırlar.
Ters orantı problemlerinde ifadeler karşılıklı olarak çarpılırlar.
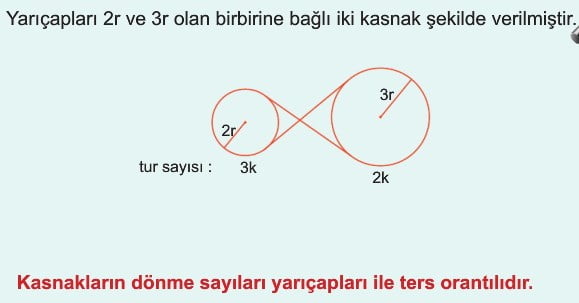
Kasnak sorularında kasnağın yarıçapı ile dönme sayısı ters orantılıdır.
İçerisinde hem ters orantı hem de doğru orantı bulunduran bileşik orantı sorularında yapılan işlerin oranı diğer ifadelerin oranına eşittir.
Örnek: Bir işçi 60 sandalyeyi 24 günde yapıyorsa 10 sandalyeyi kaç günde yapar?
Çözüm: Orantı kurduğumuzda zaman ile yapılan iş doğru orantılı olduğundan çapraz olarak çarparsak cevabı 4 gün olarak buluruz.
Örnek: Yarıçapları sırasıyla 4r ve 6r olan 2 kasnak birbirine bağlıdır. Kasnakların toplam dönme sayıları 35 olduğuna göre büyük kasnak kaç kez dönmüştür?
Çözüm: 3k ve 2k olan tur sayılarını toplarsak 5k eşittir 35 olur. Buradan k eşittir 7 bulunur. Büyük kasnak daha az döneceği için 2k eşittir 14 bulunur.
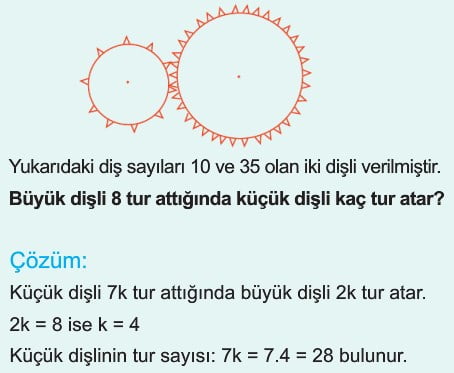
Örnek: Yukarıdaki diş sayıları 10 ve 35 olan iki dişli verilmiştir. Büyük dişli 8 tur attığında küçük dişli kaç tur atar?
Çözüm: Küçük dişli 7k tur attığında büyük dişli 2k tur atar. 2k sekize eşit olduğundan k 4 bulunur. Buradan küçük dişlinin tur sayısı 28 olarak bulunur.
Örnek: x sayısı, y sayısı ile doğru z sayısı ile ters orantılıdır. Z 2 ye eşit ve y 4 e eşit iken x sayısı 6 olduğuna göre, x sayısının 4 ve y sayısının 8 olduğu zaman z sayısının kaç olacağını bulunur.
Çözüm: x ve doğru, z ters orantılı olduğundan dolayı x eşittir y bölü z çarpı k şeklinde yazılabilir. Buradan verilen değerleri yerlerine yazdığımızda k sayısı 3 olarak bulunur. Son olara x eşittir y böl z çarpı k eşitliğini yazıp verilen değerleri yerlerine yazarsak z 6 ya eşit bulunur.