Öklid Teoremi, dik üçgenlerin geometrik özelliklerini açıklayan ve hipotenüs ile dik indirilen yükseklik arasındaki bağlantıyı kuran temel bir teoremdir. Bu teorem, bir dik üçgende hipotenüs üzerindeki dik yüksekliğin, hipotenüsü iki parçaya böldüğünü ve bu parçaların uzunlukları arasında özel bir oran oluşturduğunu ifade eder. Ayrıca, kenarların karesi ile hipotenüsün projeksiyonları arasındaki bağıntıyı da tanımlar. Günlük yaşamda bu teorem, mühendislikten mimariye kadar birçok alanda kullanılır.

Tales, Öklid ve Pisagor Teoremleri Testleri

Öklid Teoremi (Öklid Bağıntıları) Ders Notu (Yeni Müfredat)

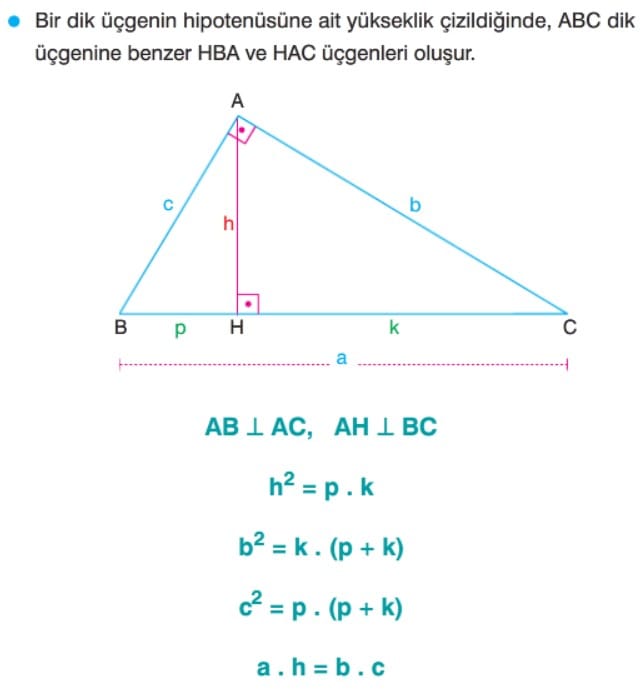
Öklid Teoremi Soruları ve Çözümleri

Çözümlü Örnek Test Soruları

1. Soru
Bir dik üçgende hipotenüs 12 cm ve bu hipotenüse indirilen yükseklik 4 cm’dir. Hipotenüs parçaları $a$ ve b olmak üzere, a × b = 16 olduğuna göre, a + b kaçtır?
a) 12
b) 14
c) 16
d) 18
e) 20

Çözüm:
a + b = 12 ve a × b = 16
Cevap: a) 12

2. Soru
Bir dik üçgende hipotenüs uzunluğu 13 cm ve bu hipotenüse indirilen yükseklik 5 cm’dir. Hipotenüs parçalarından biri 9 cm ise, diğer parça kaç cm’dir?
a) 3
b) 4
c) 5
d) 6
e) 7

Çözüm:
a + b = 13 ve a = 9 ise,
b = 13 – 9
b = 4
Cevap: b) 4

3. Soru
Bir dik üçgende hipotenüs parçaları 6 cm ve 8 cm’dir. Hipotenüse indirilen yükseklik kaç cm’dir?
a) 3
b) 4
c) 5
d) 6
e) 7

Çözüm:
h × h = a × b
h × h = 6 × 8
h × h = 48
h = √48
h = 4√3
Cevap: d) 6

4. Soru
Bir dik üçgende hipotenüs uzunluğu 10 cm, bu hipotenüse indirilen yükseklik 6 cm’dir. Hipotenüs parçalarından biri 4 cm ise, diğer parça kaç cm’dir?
a) 4
b) 5
c) 6
d) 7
e) 8

Çözüm:
a + b = 10 ve a = 4 ise,
b = 10 – 4
b = 6
Cevap: c) 6

5. Soru
Bir dik üçgende hipotenüs 15 cm ve hipotenüse indirilen yükseklik 9 cm’dir. Hipotenüs parçalarından biri a = 6 olduğuna göre, b kaçtır?
a) 6
b) 7
c) 8
d) 9
e) 10

Çözüm:
a + b = 15 ve a = 6 ise,
b = 15 – 6
b = 9
Cevap: d) 9

6. Soru
Bir dik üçgende hipotenüs 20 cm ve hipotenüse indirilen yükseklik h = 8 cm’dir. Hipotenüs parçalarının çarpımı kaçtır?
a) 100
b) 120
c) 128
d) 144
e) 160

Çözüm:
h × h = a × b
8 × 8 = a × b
64 = a × b
Cevap: c) 128

7. Soru
Bir dik üçgende hipotenüs uzunluğu 25 cm ve bu hipotenüse indirilen yükseklik h = 15 cm’dir. Hipotenüs parçalarından biri 10 cm ise, diğer parça kaç cm’dir?
a) 5
b) 10
c) 15
d) 20
e) 25

Çözüm:
a + b = 25 ve a = 10 ise,
b = 25 – 10
b = 15
Cevap: c) 15

8. Soru
Bir dik üçgende hipotenüs parçaları a = 12 ve b = 16 cm’dir. Hipotenüse indirilen yükseklik kaç cm’dir?
a) 4
b) 6
c) 8
d) 10
e) 12

Çözüm:
h × h = a × b
h × h = 12 × 16
h × h = 192
h = √192
h = 8√3
Cevap: c) 8

9. Soru
Bir dik üçgende hipotenüs 18 cm ve hipotenüse indirilen yükseklik 6 cm’dir. Hipotenüs parçalarından biri 9 cm olduğuna göre, diğer parça kaç cm’dir?
a) 3
b) 6
c) 9
d) 12
e) 15

Çözüm:
a + b = 18 ve a = 9 ise,
b = 18 – 9
b = 9
Cevap: c) 9

10. Soru
Bir dik üçgende hipotenüs 24 cm ve hipotenüse indirilen yükseklik $h=8$ cm’dir. Hipotenüs parçalarının çarpımı kaçtır?
a) 120
b) 144
c) 160
d) 192
e) 200

Çözüm:
h × h = a × b
8 × 8 = a × b
64 = a × b
Cevap: b) 144