Mutlak Değer 9. Sınıf Matematik
Mutlak Değer Fonksiyonları ve Nitel Özellikleri Yeni Müfredat
Bu yazımızda 9. sınıf müfredatında yer alan Mutlak Değer, Mutlak Değerli Denklem ve Eşitsizlikler konu anlatımı bulunmaktadır. Konu anlatımını bitirdikten sonra Mutlak Değerli Denklem ve Eşitsizlikler Soruları ve Çözümleri yazımıza tıklayarak konu ile ilgili çözümlü sorulara bakabilirsiniz.
Bunlarda İşinize Yarayabilir
Mutlak Değer Nedir?
Sayı doğrusu üzerindeki herhangi bir x reel sayısının başlangıç noktasına (orjin) olan uzaklığına x sayısının mutlak değeri denir ve |x| ile gösterilir. Mutlak değer uzaklık belirttiğinden dolayı her zaman pozitif bir gerçek sayıya eşittir. Buradan anlaşılacağı üzere pozitif ifadelerin mutlak değeri kendisine, negatif ifadelerin mutlak değeri ise ters işaretlisine (başına eksi yazılır) eşittir. Yine mutlak değer uzaklık belirttiği için alabileceği en küçük değer sıfırdır.
Örneğin;
|-5| = 5,
|7| = 7,
|0| = 0,
|-12| = 12 olur.
Bilgi: Mutlak değerin içindeki ifadenin değeri pozitif ise mutlak değerin dışına aynen çıkar, negatif ise önüne (-) alarak çıkar.
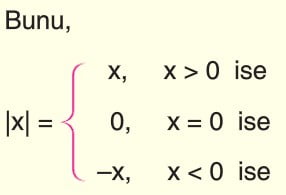
şeklinde gösterebiliriz. Her x reel sayısı için |x| ≥ 0 olur.
Örneğin;
|7| = 7,
|-4| = -(-4) = 4,
|√2 – 1| = √2 – 1 (√2 > 1 olduğuna dikkat edin.)
|√3 – 2| = -(√3 – 2) = -√3 + 2 (√3 < 2 olduğuna dikkat edin.)
Mutlak Değerin Özellikleri


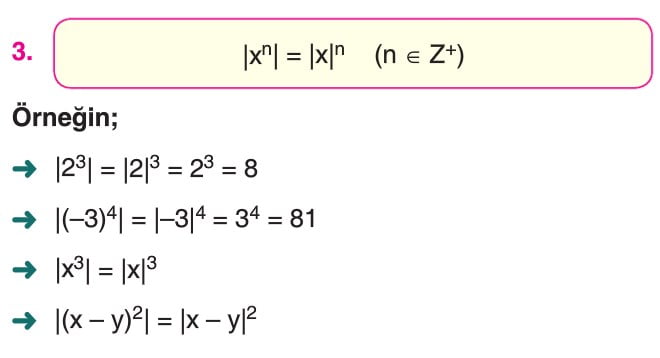


Uyarı: |f(x)| = g(x) şeklindeki ifadelerde f(x) = g(x) ve f(x) = -g(x) denklemleri çözülüp bulunan x değerlerinin denklemi sağlayıp sağlamadığı kontrol edilmelidir.
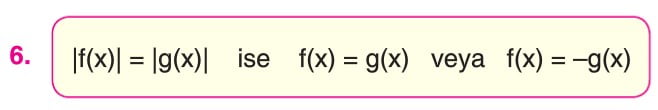
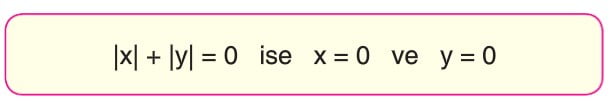



Mutlak Değer Çözümlü Örnekler
Mutlak Değerli Denklemler

Mutlak Değerli Denklemler Çözümlü Örnekler
Mutlak Değerli Eşitsizlikler



Mutlak Değerli Eşitsizlikler Çözümlü Sorular
Çözümlü Örnek Sorular:
Soru 1
|x – 3| = 7 denklemini sağlayan x değerlerini bulunuz.
Çözüm:
Mutlak değer içindeki ifade hem pozitif hem de negatif olabilir.
- x – 3 = 7 ise x = 10
- x – 3 = -7 ise x = -4
Cevap: x = 10 ve x = -4
Soru 2
|2x + 5| = 9 denklemini sağlayan x değerlerini bulunuz.
Çözüm:
- 2x + 5 = 9 ise 2x = 4, x = 2
- 2x + 5 = -9 ise 2x = -14, x = -7
Cevap: x = 2 ve x = -7
Soru 3
|x + 6| + 4 = 12 denklemini sağlayan x değerlerini bulunuz.
Çözüm:
Öncelikle mutlak değeri yalnız bırakmak için her iki taraftan 4 çıkaralım:
|x + 6| = 8
- x + 6 = 8 ise x = 2
- x + 6 = -8 ise x = -14
Cevap: x = 2 ve x = -14
Soru 4
|3x – 9| = 12 denklemini sağlayan x değerlerini bulunuz.
Çözüm:
- 3x – 9 = 12 ise 3x = 21, x = 7
- 3x – 9 = -12 ise 3x = -3, x = -1
Cevap: x = 7 ve x = -1
Soru 5
Aşağıdaki mutlak değer ifadesinin sonucunu bulunuz:
|4 – x| = 6
Çözüm:
- 4 – x = 6 ise -x = 2, x = -2
- 4 – x = -6 ise -x = -10, x = 10
Cevap: x = -2 ve x = 10
Soru 6
Aşağıdaki eşitsizliği sağlayan x değerlerini bulunuz:
|x – 5| < 4
Çözüm:
Mutlak değer ifadesi küçük bir sayıya eşitse, ifade -4 ile 4 arasında olmalıdır:
-4 < x – 5 < 4
Bu eşitsizliği çözelim:
- Her iki tarafa 5 ekleyelim: -4 + 5 < x < 4 + 5
- 1 < x < 9
Cevap: 1 < x < 9

































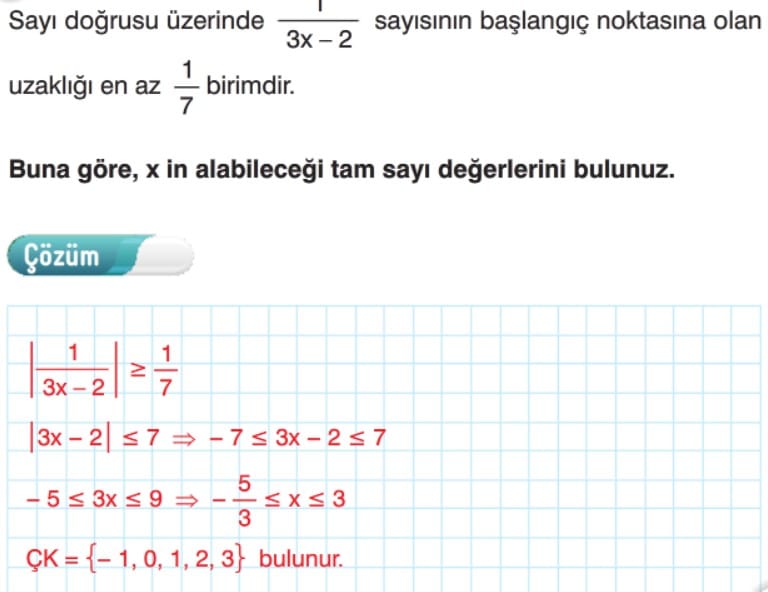



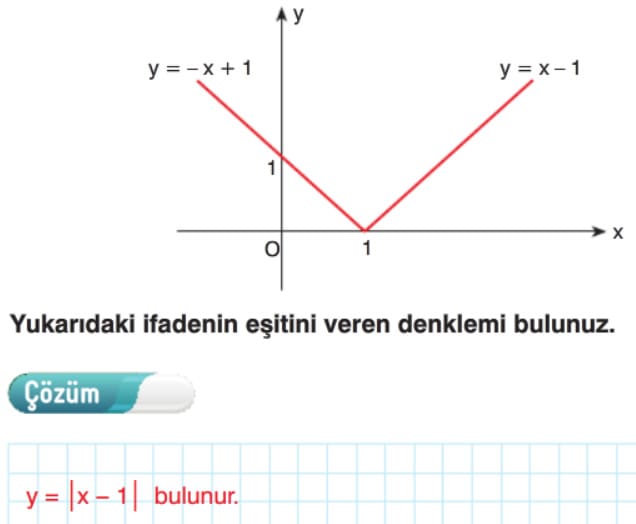


Güzel anlatıyorlar ben bğendim kolaymış.ödevlerim konusunda da yardımcı oluyo bu com iyi oldu beyendim👍
Okulda bir iki noktayı kaçırmıştım. Bu anlatım iyi geldi. Kaçırdığım yerleri şimdi tam olarak anlayabildim. Zaten kolay bir konuymuş. Hiç zorlanmadım 🙂