9. Sınıf Mantık Dağılma Özelliği

iki veya daha fazla önermeyle oluşturulmuş bir birleşik önermenin, bu önermelerin her biri ile ayrı ayrı birleştirildiğinde aynı sonucu vereceğini belirten bir özelliktir.

9. Sınıf Mantık De Morgan Kuralları

Çözümlü Sorular

Sonraki konu olan Ya da Bağlacı ve Özellikleri konusuna gitmek için bağlantıya tıklayın.

9. Sınıf Mantık Dağılma Özelliği ve De Morgan Kuralları

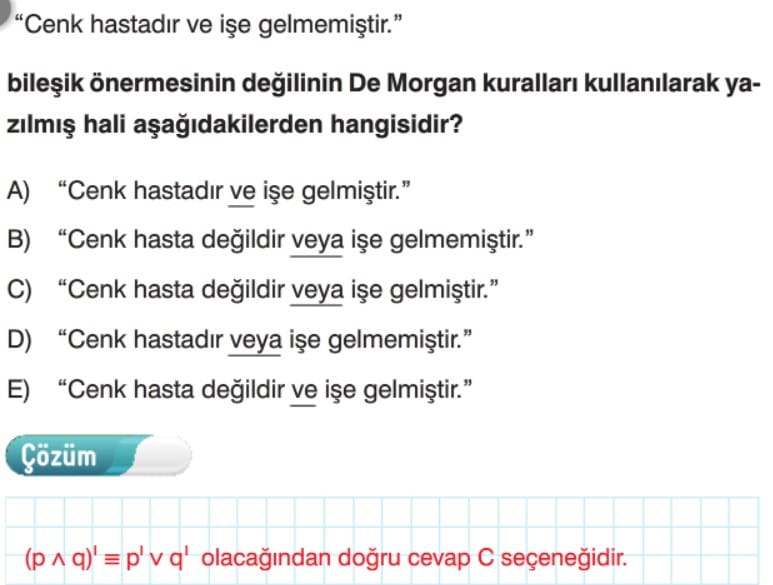
Çözümlü Örnek Test Soruları

Mantık Dağılma Özelliği ve De Morgan Kuralları

Soru 1: A ve B önermeleri için De Morgan kuralına göre, ¬(A ∧ B) ifadesi nasıl yazılır?
A) ¬A ∧ ¬B
B) ¬A ∨ ¬B
C) ¬A ∧ B
D) A ∨ B
Cevap: B
Çözüm: De Morgan kuralına göre, ¬(A ∧ B) = ¬A ∨ ¬B olarak yazılır.

Soru 2: ¬(A ∨ B) ifadesinin De Morgan kuralına göre eşdeğeri nedir?
A) ¬A ∧ ¬B
B) ¬A ∨ B
C) A ∧ ¬B
D) ¬A ∨ ¬B
Cevap: A
Çözüm: De Morgan kuralına göre, ¬(A ∨ B) = ¬A ∧ ¬B olur.

Soru 3: Aşağıdaki ifadelerden hangisi ¬(P ∨ Q) ifadesine denktir?
A) P ∧ Q
B) ¬P ∧ Q
C) ¬P ∧ ¬Q
D) P ∨ ¬Q
Cevap: C
Çözüm: De Morgan kuralına göre, ¬(P ∨ Q) = ¬P ∧ ¬Q olarak yazılır.

Soru 4: A ve B önermeleri için dağılma özelliğine göre A ∧ (B ∨ C) ifadesi nasıl açılır?
A) (A ∧ B) ∨ C
B) A ∨ B ∨ C
C) (A ∧ B) ∨ (A ∧ C)
D) A ∧ B ∧ C
Cevap: C
Çözüm: Dağılma özelliğine göre A ∧ (B ∨ C) = (A ∧ B) ∨ (A ∧ C) olarak açılır.

Soru 5: De Morgan kurallarına göre, ¬(A ∧ B) ifadesinin eşdeğeri nedir?
A) ¬A ∧ B
B) ¬A ∨ ¬B
C) ¬A ∨ B
D) A ∨ B
Cevap: B
Çözüm: De Morgan kuralına göre ¬(A ∧ B) = ¬A ∨ ¬B ifadesi elde edilir.

Soru 6: (A ∨ B) ∧ (A ∨ C) ifadesi dağılma özelliğine göre nasıl sadeleştirilir?
A) A ∨ (B ∧ C)
B) A ∧ B ∧ C
C) (A ∧ B) ∨ C
D) A ∧ (B ∨ C)
Cevap: A
Çözüm: Dağılma özelliğine göre (A ∨ B) ∧ (A ∨ C) = A ∨ (B ∧ C) olarak sadeleştirilir.

Soru 7: De Morgan kurallarından yararlanarak, ¬(P ∧ Q) ifadesinin eşdeğerini bulunuz.
A) P ∨ Q
B) ¬P ∨ ¬Q
C) ¬P ∧ ¬Q
D) ¬P ∨ Q
Cevap: B
Çözüm: De Morgan kuralına göre ¬(P ∧ Q) = ¬P ∨ ¬Q ifadesi elde edilir.

Soru 8: A ∨ (B ∧ C) ifadesini dağılma özelliğini kullanarak açınız.
A) (A ∨ B) ∧ (A ∨ C)
B) (A ∧ B) ∨ C
C) A ∧ B ∧ C
D) A ∨ B ∨ C
Cevap: A
Çözüm: Dağılma özelliğine göre A ∨ (B ∧ C) = (A ∨ B) ∧ (A ∨ C) olarak açılır.

Matematik dersi yeni müfredatı ile mantık konusu 9. sınıfların ilk konusu oldu. Bu yazımızda mantık dersi dağılma özelliği ve de morgan kuralları konu anlatımı ve soru çözümlerini sizlerle paylaşıyoruz.
Ve işleminin veya işlemi üzerinde sağdan ve soldan dağılma özelliği vardır. Veya işleminin de ve işlemi üzerinde sağdan ve soldan dağılma özelliği vardır. Kurallar konuda verilmiştir.
De morgan kuralları ise ve ile veya bağlacı ile bağlanmış olan bileşik önermelerin değillerini (olumsuzlarını) almamıza yarayan kurallardır. De morgan kurallarında ilk bileşenin değili alınır, veya işlemi ve, ve işlemi de veya işlemine dönüştükten sonra ikinci bileşenin değili alınır. De morgan kuralları sözel olarak bu şekilde ifade edilebilir. Sembolik olarak de morgan kuralları konuda verilmiştir.
Konu içeriğinde de morgan kuralları ve dağılma özelliği ile ilgili olarak çeşitli örnek soru çözümleri yer almaktadır. Bu örnekleri inceleyerek konuyu daha iyi kavrayabilirsiniz.