Logaritma Fonksiyonunun Özellikleri 12. sınıf Matematik
Logaritma fonksiyonu, matematikte önemli bir yer tutan ve çeşitli hesaplamalarda sıkça kullanılan bir fonksiyondur. Logaritma, bir sayının tabanına göre hangi üssü alması gerektiğini belirten bir işlemdir ve genellikle şeklinde tanımlanır; burada a logaritmanın tabanıdır ve x pozitif bir sayıdır. Logaritma fonksiyonunun bazı temel özellikleri vardır: Öncelikle, logaritma fonksiyonu sadece pozitif sayılar için tanımlıdır. Ayrıca, logaritma fonksiyonu artandır, yani x değerleri arttıkça y değeri de artar. Tabanın değeri 1’den büyükse, fonksiyonun grafiği her zaman x eksenini keser ve asimptot olarak y eksenine yaklaşır. Logaritmanın temel özellikleri arasında çarpma ve bölme işlemleri için toplama ve çıkarma yapma yeteneği, üslü ifadelerin logaritmasının logaritma fonksiyonu kullanılarak düzenlenmesi ve belirli logaritma değerlerinin hesaplanması yer alır. Bu ders notları, logaritma fonksiyonunun özelliklerini detaylı bir şekilde inceleyerek, öğrencilerin bu kavramı daha iyi anlamalarına ve matematiksel problemleri çözme becerilerini geliştirmelerine yardımcı olmayı amaçlamaktadır.
Logaritma Konuları
- Logaritma Fonksiyonu ve grafiği
- 10 ve e Tabanında Logaritma Fonksiyonu
- Logaritma Fonksiyonunun Özellikleri
- Üstel, Logaritmik Denklemler ve Eşitsizlikler
- Üstel ve Logaritmik Fonksiyon Problemleri
12. sınıf Logaritma Fonksiyonunun Özellikleri Ders Notu


Logaritma Fonksiyonunun Özellikleri Soruları ve Çözümleri
Taban Değiştirme
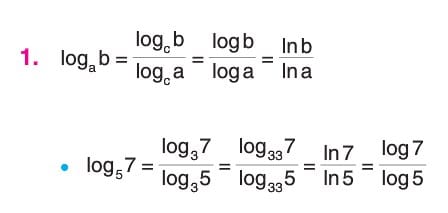
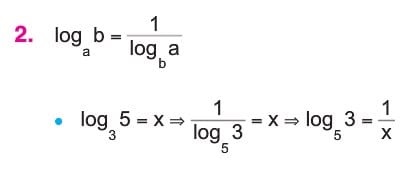

Logaritma Fonksiyonunun Özellikleri Soruları ve Çözümleri
Çözümlü Örnek Test Soruları
1. log₅25 + log₃9 işleminin sonucu kaçtır?
A) 3
B) 4
C) 5
D) 6
Çözüm:
- log₅25 = log₅5² = 2
- log₃9 = log₃3² = 2
- Toplam: 2 + 2 = 4
Doğru Cevap: B
2. log₂(x – 3) = 4 denklemini sağlayan x değeri kaçtır?
A) 13
B) 16
C) 19
D) 21
Çözüm:
- log₂(x – 3) = 4 ⇒ x – 3 = 2⁴
- x – 3 = 16 ⇒ x = 19
Doğru Cevap: C
3. logₐb = 2 ve logₐc = 3 olduğuna göre, logₐ(b²c³) ifadesinin değeri kaçtır?
A) 13
B) 15
C) 17
D) 19
Çözüm:
- logₐ(b²c³) = 2logₐb + 3logₐc
- = 2(2) + 3(3) = 4 + 9 = 13
Doğru Cevap: A
4. log₅(2x – 1) = log₅(x + 3) denkleminin çözüm kümesi nedir?
A) {4}
B) {5}
C) {6}
D) {7}
Çözüm:
- logₐM = logₐN ⇒ M = N
- 2x – 1 = x + 3 ⇒ x = 4
- Kontrol: 2(4) – 1 > 0 ve 4 + 3 > 0 (Sağlanır)
Doğru Cevap: A
5. log₂3 ≈ 1,585 olduğuna göre, log₈9 ifadesinin yaklaşık değeri kaçtır?
A) 1,056
B) 1,585
C) 2,585
D) 3,170
Çözüm:
- log₈9 = log₂9 / log₂8 = (2log₂3)/3
- = (2 × 1,585)/3 ≈ 3,170/3 ≈ 1,056
Doğru Cevap: A


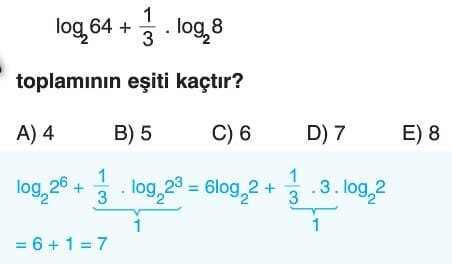




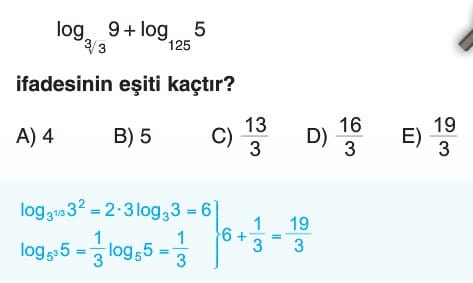








çok işime yaradı teşeşkkürler.