Limit ve süreklilik, matematikte önemli kavramlar olup, bir fonksiyonun belirli bir noktada davranışını ve kesintisizliğini analiz etmek için kullanılır. Limit, bir fonksiyonun bir noktaya yaklaşırken aldığı değerleri ifade ederken, süreklilik ise fonksiyonun bir aralıkta kesintisiz bir şekilde devam etmesini tanımlar. Bu kavramlar, özellikle kalkülüs alanında, diferansiyasyon ve entegrasyon işlemlerinin temelini oluşturur. Limit ve süreklilik, matematiksel analizde ve uygulamalı bilimlerde kritik rol oynayarak, fonksiyonların grafiklerini anlamamıza ve çözümlememize yardımcı olur.

12. Sınıf Limit ve Süreklilik Ders Notu

A) Limit Kavramı

Bir x değişkeni, sayı doğrusunda;

• a değerine, a dan küçük değerlerle yaklaşıyorsa “x’in a’ya soldan yaklaşması” şeklinde ifade edilir ve “x → a^–” şeklinde gösterilir.
• a değerine, a dan büyük değerlerle yaklaşıyorsa “x’in a’ya sağdan yaklaşması” şeklinde ifade edilir ve “x → a⁺” şeklinde gösterilir.

Örneğin; Bir futbolcunun attığı gol ortalaması
1. sezon; 0,85
2. sezon; 0,88
3. sezon; 0,91
4. sezon; 0,94
5. sezon; 0,97
şeklindeyse ortalama 1 ‘e soldan yaklaşıyor demektir.

Dikkat:

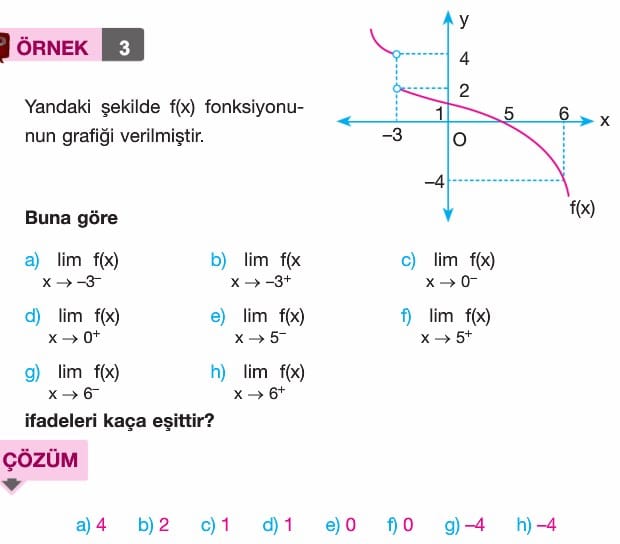
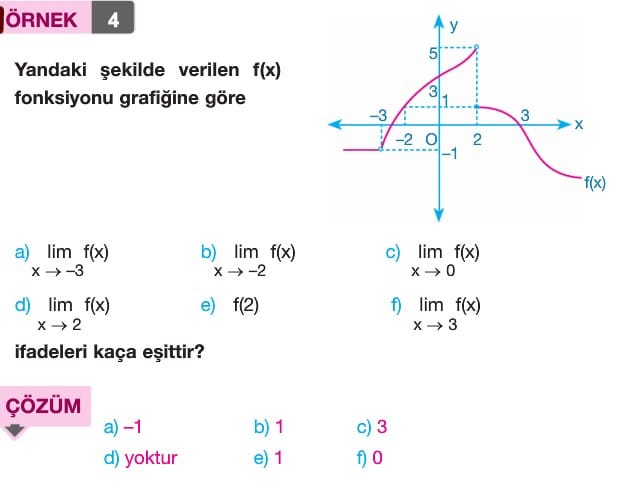
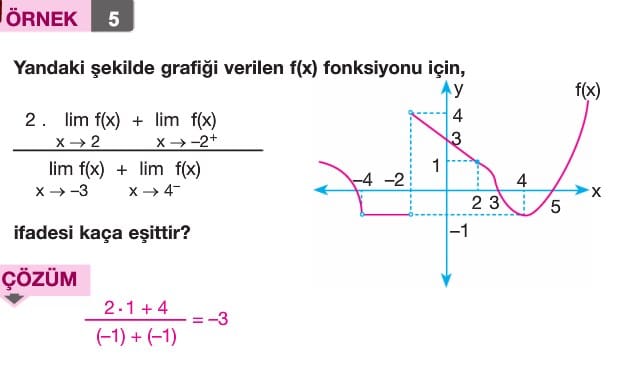
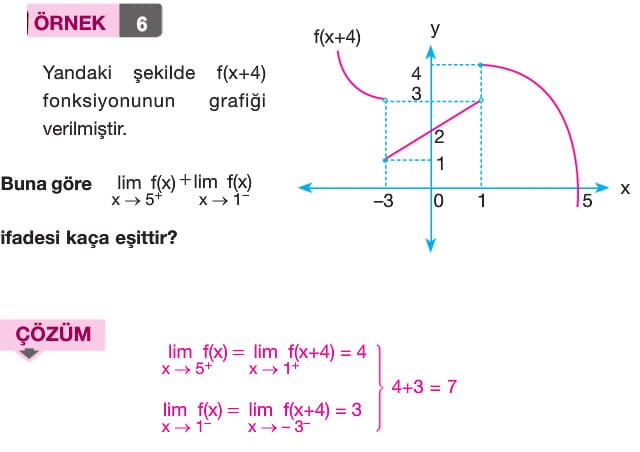
Çözümlü Sorular

Dikkat:

Dikkat:

Dikkat:

Çözümlü Sorular

B) Limitin Özellikleri

Çözümlü Sorular

Çözümlü Sorular

Çözümlü Sorular

Çözümlü Sorular

C) Parçalı Fonksiyonun Limiti

Belirli reel sayı aralıklarına göre tanımlamaları yapılmış bir parçalı fonksiyonda bu aralıkların sınır değerleri olan gerçek sayılar fonksiyonun kritik noktalarıdır.

• Kritik noktalar dışındaki herhangi bir gerçek sayı için fonksiyonun limitini bulmak istersek; “gerçek sayının bulunduğu aralık için tanımlanan fonksiyonun, bu gerçek sayı için limiti bulunur.”
  

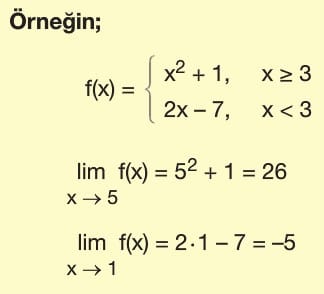
Dikkat:

• Kritik noktalar için limit incelemesi yapılırken, kritik nokta için sağdan ve soldan limit incelenir. “Kritik nokta için sağdan limit ile soldan limit aynı L değerine eşit oluyorsa, kritik nokta için fonksiyonun limiti L olur.”
  

Dikkat: Kritik nokta için sağdan ve soldan limit incelemesi sonucunda; “sağdan limit ile soldan limit farklı değerler çıkıyorsa bu kritik nokta için fonksiyonun limiti yoktur.“

Çözümlü Sorular

D) Mutlak Değer Fonksiyonunun Limiti

Bir mutlak değer fonksiyonunda bulunan mutlak değer içindeki ifadeyi sıfırlayan gerçek sayı, bu fonksiyonun kritik noktasıdır.

• Kritik noktalar dışındaki herhangi bir gerçek sayı için fonksiyonun limitini bulmak istersek; “Bu gerçek sayıyı fonksiyonda doğrudan yerine yazıp sonucu buluruz.”
  
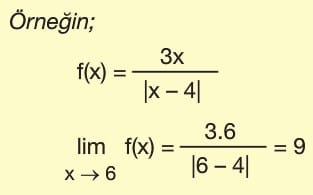
• Kritik noktalar için limit incelemesi yapılırken, kritik nokta için sağdan ve soldan limit incelenir. “Kritik nokta için sağdan limit ile soldan limit aynı L değerine eşit oluyorsa, kritik nokta için fonksiyonun limiti L olur.”
  

Dikkat: Kritik nokta için sağdan ve soldan limit incelemesi sonucunda; “sağdan limit ile soldan limit farklı değerler çıkıyorsa bu kritik nokta için fonksiyonun limiti yoktur.”

Çözümlü Sorular

E) 0/0 Belirsizliği

Dikkat: Pay veya paydada köklü ifadelerin bulunması durumunda sadeleştirme işleminden önce “pay ve paydayı eşlenikle çarpmak” gerekebilir.

Çözümlü Sorular

E) Süreklilik

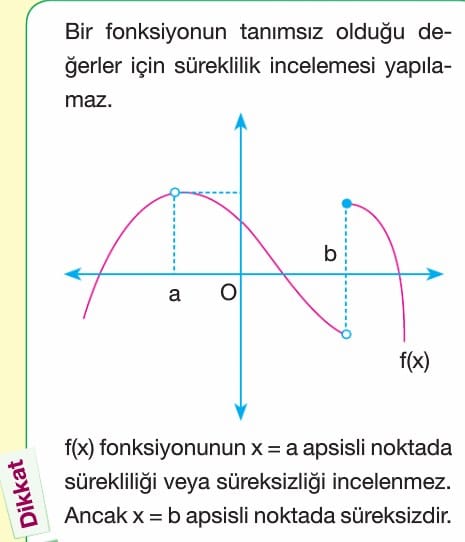
Çözümlü Sorular

Çözümlü Test Soruları

1. lim(x→3) (x² – 9)/(x – 3) limitinin değeri kaçtır?
A) 0
B) 3
C) 6
D) Limit yoktur

Çözüm: Doğru cevap C seçeneğidir.
(x² – 9)/(x – 3) = (x – 3)(x + 3)/(x – 3) = x + 3 (x ≠ 3)
lim(x→3) (x + 3) = 6

2. f(x) = { 2x + 1, x < 2
{ 5, x = 2
{ x², x > 2
fonksiyonunun x = 2 noktasındaki limiti nedir?
A) 4
B) 5
C) 6
D) Limit yoktur

Çözüm: Doğru cevap D seçeneğidir.
Sağdan limit: lim(x→2⁺) x² = 4
Soldan limit: lim(x→2⁻) (2x + 1) = 5
Limitler farklı olduğu için limit yoktur.

3. lim(x→∞) (3x² + 2x – 5)/(2x² – x + 1) limitinin değeri kaçtır?
A) 0
B) 1/2
C) 3/2
D) ∞

Çözüm: Doğru cevap C seçeneğidir.
Pay ve paydayı x²’ye bölersek:
(3 + 2/x – 5/x²)/(2 – 1/x + 1/x²) → 3/2 (x→∞ iken diğer terimler 0 olur)

4. f(x) = |x – 3| fonksiyonu için aşağıdakilerden hangisi doğrudur?
A) x=3’te süreklidir ama türevlenebilir değildir
B) x=3’te süreksizdir
C) x=3’te türevlenebilirdir
D) Hiçbir noktada sürekli değildir

Çözüm: Doğru cevap A seçeneğidir.
Mutlak değer fonksiyonu x=3’te süreklidir (V şeklinde) ancak bu noktada köşe oluştuğu için türev yoktur.

5. lim(x→0) (sin5x)/3x limitinin değeri kaçtır?
A) 0
B) 1/3
C) 5/3
D) 1

Çözüm: Doğru cevap C seçeneğidir.
lim(x→0) sin(ax)/bx = a/b kuralına göre:
sin5x/3x → 5/3

6. f(x) = (x² – 4)/(x – 2) fonksiyonu için aşağıdakilerden hangisi doğrudur?
A) x=2’de süreklidir
B) x=2’de süreksizdir (kaldırılabilir)
C) x=2’de süreksizdir (sonsuz)
D) Hiçbir noktada sürekli değildir

Çözüm: Doğru cevap B seçeneğidir.
f(x) = (x – 2)(x + 2)/(x – 2) = x + 2 (x ≠ 2)
x=2’de tanımsız olduğu için süreksizdir, ancak limit var olduğundan bu süreksizlik kaldırılabilir türdendir.